TRƯỜNG THPT CHUYÊN LƯƠNG VĂN CHÁNH
TỔ TOÁN
ĐỀ THI THỬ TUYỂN SINH ĐẠI HỌC NĂM 2009
MÔN TOÁN – KHỐI D
(Thời gian làm bài: 180 phút)
PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 điểm)
Câu I. (2,0 điểm)
Cho hàm số
42
22yx x=− +
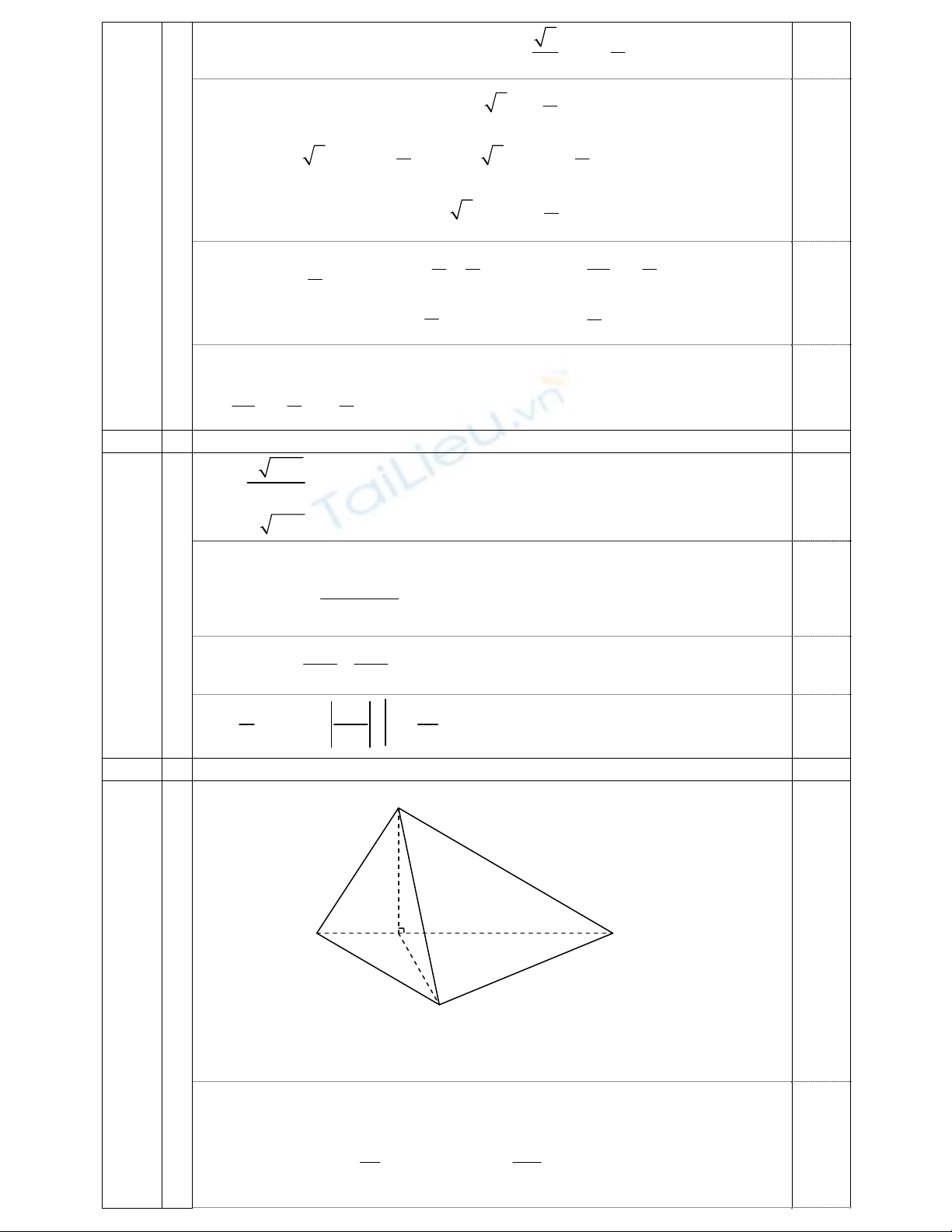
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2. Viết phương trình các tiếp tuyến kẻ đến đồ thị (C), biết rằng các tiếp tuyến này đi qua
điểm A(0; 2)
Câu II. (2,0 điểm)
1. Giải bất phương trình:
()
(
)
22
2log log 6
2 3.2 1
xx
xx
−+
−
+
>
2. Giải phương trình:
()
22
2
sinx+cosx 2sin 2sin sin 3
1 cot 2 4 4
x
x
x
x
ππ
−⎛⎞
⎛⎞⎛
=−−−
⎜⎟⎜⎜⎟
+⎝⎠⎝
⎝⎠
⎞
⎟
⎠
Câu III. (1,0 điểm) Tính tích phân:
2
1
1
5
xx
I
dx
x
−
=−
∫
Câu IV. (1,0 điểm)
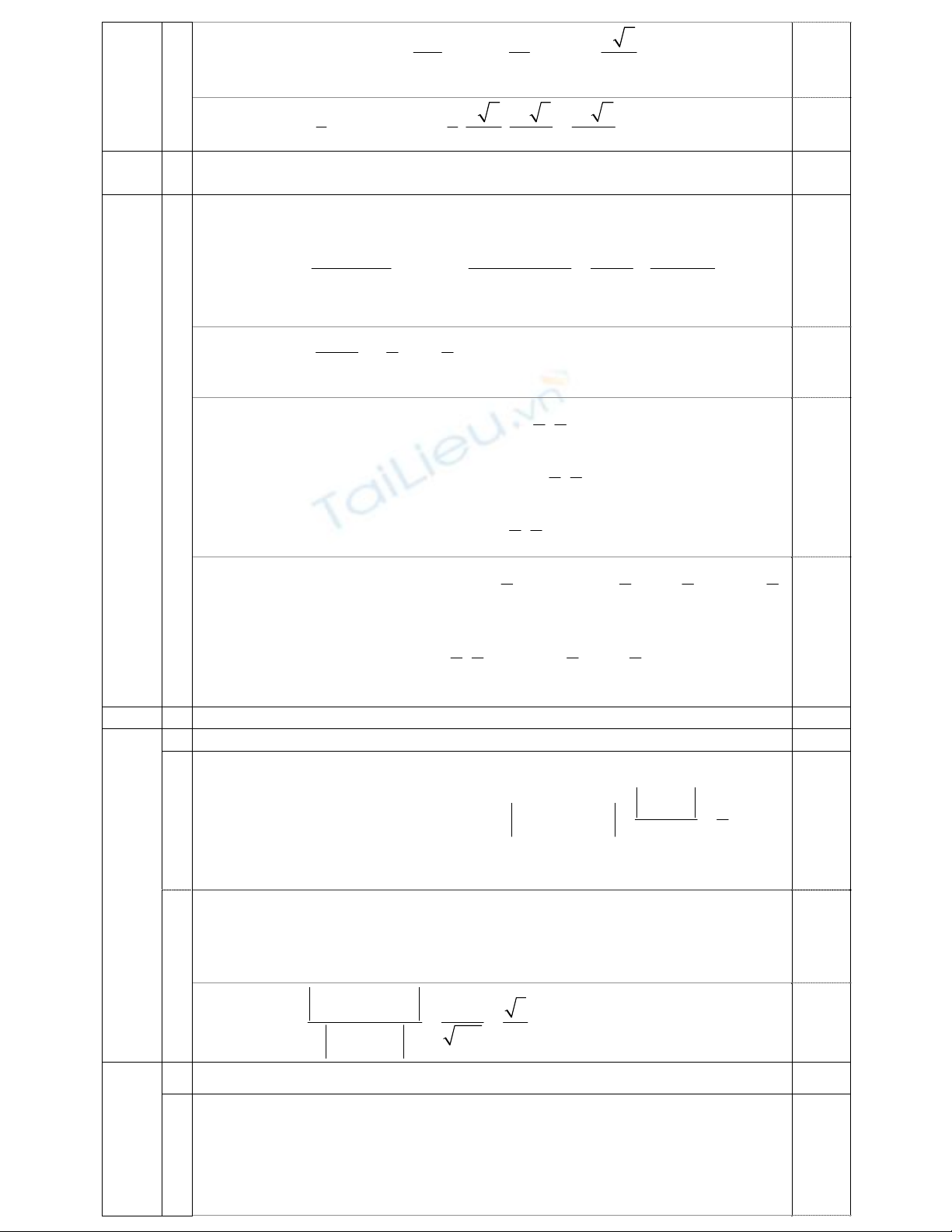
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, tam giác SAC cân tại S, góc SBC bằng
0
60 , mặt phẳng (SAC) vuông góc với mặt phẳng (ABC). Tính theo a thể tích của khối chóp
S.ABC.
Câu V. (1,0 điểm) Tìm m để phương trình sau có nghiệm thực:
()
2
32 2
10xxxmx
+
+− + =
PHẦN RIÊNG (3,0 điểm)
Thí sinh chỉ được làm một trong hai phần (phần 1 hoặc phần 2)
1. Theo chương trình Chuẩn:
Câu VI.a (2,0 điểm) Trong không gian với hệ toạ độ Oxyz, cho các điểm
()()
(
)
(
)
1; 1; 0 , 1; 1; 2 , 2; 2;1 , 1;1;1ABCD−− − − − .
1. Tính góc và khoảng cách giữa các đường thẳng AB và CD.
2. Giả sử
()
α
là mặt phẳng đi qua D và cắt ba trục toạ độ Ox, Oy, Oz tương ứng tại các
điểm M, N, P khác gốc O sao cho D là trực tâm của tam giác MNP. Hãy viết phương
trình của mặt phẳng
()
α
Câu VII.a (1,0 điểm)
Cho a, b, c là các số thực dương thoả mãn ab + bc + ca = 3.
Chứng minh rằng:
() () ()
222
111
111a b c b a c c b a abc
++
++ ++ ++
1
≤
2. Theo chương trình Nâng cao:
Câu VI.b (2,0 điểm)
Trong không gian với hệ toạ độ Oxyz, cho các điểm
()()
(
)
(
)
(
)
1; 1; 0 , 1; 1; 2 , 2; 2;1 , 1;1;1 , 4; 2;1ABCDE−− − − − .
1. Tính góc và khoảng cách giữa các đường thẳng AB và CD.
2. Giả sử
()
α
là mặt phẳng đi qua E và cắt tia Ox tại M, tia Oy tại N, tia Oz tại P. Viết
phương trình mặt phẳng
()
α
khi tứ diện OMNP có thể tích nhỏ nhất.
Câu VII.b (1,0 điểm) Tìm hệ số của 10
trong khai triển
(
10
3
1
1 x
x
x
⎛⎞
)
0
+
+
⎜⎟
⎝⎠
≠
-------------------------------Hết ----------------------------
TRƯỜNG THPT CHUYÊN LƯƠNG VĂN CHÁNH
TỔ TOÁN
ĐÁP ÁN - THANG ĐIỂM
ĐỀ THI THỬ TUYỂN SINH ĐẠI HỌC NĂM 2009
MÔN TOÁN – KHỐI D
Câu Đáp án Điểm
I 2,00
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1,00 điểm)
42
22yx x=− +
Tập xác định
D=\
Sự biến thiên:
(
)
32
'4 4 4 1yxxxx
=
−= −
()
2
0
'0 4 1 0 1
1
x
yxx x
x
=
⎡
⎢
=⇔ − =⇔ =−
⎢
⎢
=
⎣
0,25
Bảng biến thiên
x –∞ – 1 0 1 +∞
y’ – 0 + 0 – 0 +
y +∞ 2 +∞
1 1
0,25
() ()
(
)
CD
111, 0
CT
yy y yy=−= = = =2
0,25
1
Đồ thị:
0,25
2 Viết phương trình tiếp tuyến (1,00 điểm)
–
1 0 1
y
2
1
x
Phương trình đường thẳng (d) đi qua điểm
(
)
0; 2A có hệ số góc k là:
2
y
kx=+
(d) là tiếp tuyến của đồ thị (C) khi và chỉ khi HPT:
có nghiệm.
()
()
42
3
22 21
44 2
xx kx
xxk
⎧−+=+
⎪
⎨−=
⎪
⎩
Từ (1) và (2) suy ra:
()
42 3
42
2
2
2244
32 0
0
0
26
33
xx xxx
xx
x
x
xx
−+= − +
⇔−=
=
⎡
⎡=⎢
⎢
⇔⇔
⎢
⎢==±
⎢⎢
⎣⎣
2
0,25
0,25
* Với x = 0, thay vào (2) ta được k = 0, ta có PTTT
(
)
1:2dy
=
* Với 6
3
x=− , thay vào (2) ta được 46
9
k=,
ta có PTTT
()
2
46
:2
9
dy x
=
+
* Với 6
3
x=, thay vào (2) ta được 46
9
k=− ,
ta có PTTT
()
3
46
:2
9
dy x
=
−+
0,50
II 2,00
1 Giải bất phương trình (1,00 điểm)
()
(
)
()
22
2log log 6
23.2 11
xx
xx
−+
−
+>
Điều kiện: x > 0 (*)
Khi đó: 23
.2 2
xxx−
+>>1
0,25
(
)
(
)
(
)
(
)
22 2
1 2log log 6 log 2 3.2 0 2
xx
xx −
⎡⎤
⇔−+ +>
⎣⎦
Vì
23 , nên
.2 2
xxx−
+>>1
(
)
2
log 2 3.2 0
xx−
+
>
0,25
Do đó
(
)
(
)
(
)
2
22 2 2
2 2log log 6 0 log log 6xx x x
⎡⎤
⇔−+>⇔>
⎣⎦ +
3
22
6602xx xx x x⇔>+⇔−−>⇔<−∨>
0,25
Đối chiếu với điều kiện (*), ta được x > 3.
Vậy nghiệm của bất phương trình là x > 3.
0,25
2 Giải phương trình lượng giác (1,00 điểm)
() ()
22
2
sinx+cosx 2sin 2sin sin 3 1
1cot 2 4 4
xxx
x
ππ
−⎛⎞
⎛⎞⎛ ⎞
=−−−
⎜⎟⎜ ⎟⎜⎟
+⎝⎠⎝ ⎠
⎝⎠
Điều kiện:
()
sinx 0 *≠
0,25
PT
()
()
()
22
2
1 1 2sinxcosx 2sin .sin .2 os 2 sinx 1
24
xx c x
π
⎛⎞
⇔+ − = −
⎜⎟
⎝⎠
()
2
sin 2 os2x .sin 2 os 2 sinx
4
xc x c x
π
⎛⎞
⇔+ = −
⎜⎟
⎝⎠
2os2 .sin 2os2
44
cx xcx
π
π
⎛⎞ ⎛⎞
⇔−=
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
−
sinx 0,sin2x+cos2x= 2 os 2 4
cx
π
⎛⎞
⎛⎞
≠−
⎜⎟
⎜⎟
⎝⎠
⎝⎠
0,25
3.
2.
os 2 0 82
42
4
.2 .2
sinx=1 22
x
k
xk
cx
xm xm
π
π
ππ
ππ
ππ
π
π
⎡
⎡
⎡⎛⎞ =+
−=+ ⎢
⎢
−=
⎜⎟
⎢
⇔⇔⇔
⎢
⎢
⎝⎠
⎢⎢
⎢=+ =+
⎢
⎣⎢
⎢
⎣⎣
0,25
Đối chiếu điều kiện (*) ta có nghiệm của phương trình là:
()
3.; .2 ,
822
x
kx m kmZ
π
ππ π
=+ =+ ∈
0,25
III Tính tích phân 1,00
2
1
1
5
xx
I
dx
x
−
=−
∫
Đặt 2
11;tx xt dxtd=−⇒=+ =2t
0,25
Đổi cận: 1 0; 2 1
x
tx t
=
⇒= = ⇒=
()
22
1
2
0
21
4
tt
I
dt
t
+
⇒= −
∫
0,25
1
2
0
55
25
22
td
tt
⎛⎞
=++−
⎜⎟
−+
⎝⎠
∫t
0,25
1
3
0
232
255ln 10ln
323
tt
tt
⎛⎞
−
=++ =−
⎜⎟
+
⎝⎠
3
0,25
IV Tính thể tích 1,00
Gọi H là trung điểm của AC, suy ra
(
)
SH ABC⊥
0,25
Áp dụng định lí hàm số côsin trong tam giác SBC:
(
)
222
.1SC SB a a SB=+−
2
22
4
a
SC SH=+
và
2
22
3
4
a
SB SH=+
(2)
A
S
C
B
H
0,25
Từ (1) và (2) suy ra:
2
33
.22
aa
aSB SB SH=⇒=⇒=
6
2
a
0,25
Do đó
()
23
.
1163
...
3324
S ABC
aa a
V SH dt ABC===
2
8
0,25
V Tìm m để phương trình sau có nghiệm thực
1,00
()
()
2
32 2
101xxxmx++− + =
()
32
2
21
x
xx
mx
++
⇔= +
(
)
() ()
22 2
22
2
2
1
1
11
xx x xx
mx
xx
++
⇔= = +
+
++
2
0,25
Đặt 21
x
tx
=+, 1
22
t−≤≤
1
. Ta có phương trình :
()
22ttm+=
0,25
Xét hàm số
()
2
f
ttt
=
+, với 11
;
22
t
⎡
⎤
∈−
⎢
⎥
⎣
⎦
Ta có với mọi
()
'21ft t=+≥011
;
22
t
⎡
⎤
∈−
⎢
⎥
⎣
⎦,
nên f(t) đồng biến trên 11
;
22
⎡
⎤
−
⎢
⎥
⎣
⎦.
0,25
Do đó tập giá trị của f(t) là
() ()
111
224
fftf ft
⎛⎞ ⎛⎞ 3
4
−
≤≤ ⇔−≤≤
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
Vậy phương trình (1) có nghiệm thực khi và chỉ khi phương trình (2)
có nghiệm thuộc đoạn 11
;
22
⎡
⎤
−
⎢
⎥
⎣
⎦, do đó 13
44
m
−
≤≤
0,25
VI.a 2,00
1 Tính góc và khoảng cách giữa hai đường thẳng (1,00 điểm)
Ta có
()
(
)
2; 0; 2 , 3; 3; 0AB CD==−
JJJG JJJG
• Ta có
()
()
.1
os AB,CD os AB, .2
AB CD
ccCD
AB CD
=
==
J
JJG JJJG
JJJG JJJG .
• Vậy góc giữa AB và CD bằng .
0
60
0,50
()
(
)
(
)
()
2; 0; 2 , 3; 3; 0 , 3; 1;1
,6;6;6,,.6
AB CD AC
AB CD AB CD AC
==−=−
⎡⎤ ⎡⎤
⇒=−− =−
⎣⎦ ⎣⎦
JJJG JJJG JJJG
JJJG JJJG JJJG JJJG JJJG 0≠
0,25
()
,. 63
,3
108
,
AB CD AC
dABCD AB CD
⎡⎤
⎣⎦
==
⎡⎤
⎣⎦
JJJG JJJG JJJG
JJJG JJJG
=
0,25
2 Viết phương trình mặt phẳng
(
)
α
(1,00 điểm)
Xét các điểm
(
)
(
)
(
)
;0;0 , 0; ;0 , 0;0;
M
mNnPp
với . 0mnp ≠
Ta có
()
(
)
()()
1; 1; 1 , ; ; 0 .
1; 1; 1 , ; 0; .
DP p NM m n DP NM m n
DN n PM m p DN PM m p
⎧⎧
=− − = − =+
⎪⎪
⇒
⎨⎨
=−− = − =+
⎪
⎪⎩
⎩
JJJG JJJJG
J
JJG JJJJG
JJJG JJJJG JJJG JJJJG
0,25