TRƯỜNG THPT PHAN ðÌNH PHÙNG ðỀ THI THỬ ðẠI HỌC NĂM 2011
HÀ NỘI MÔN THI: TOÁN – KHỐI A
__________ Thời gian làm bài: 180 phút
A. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 ñiểm)
Câu I (2 ñiểm)
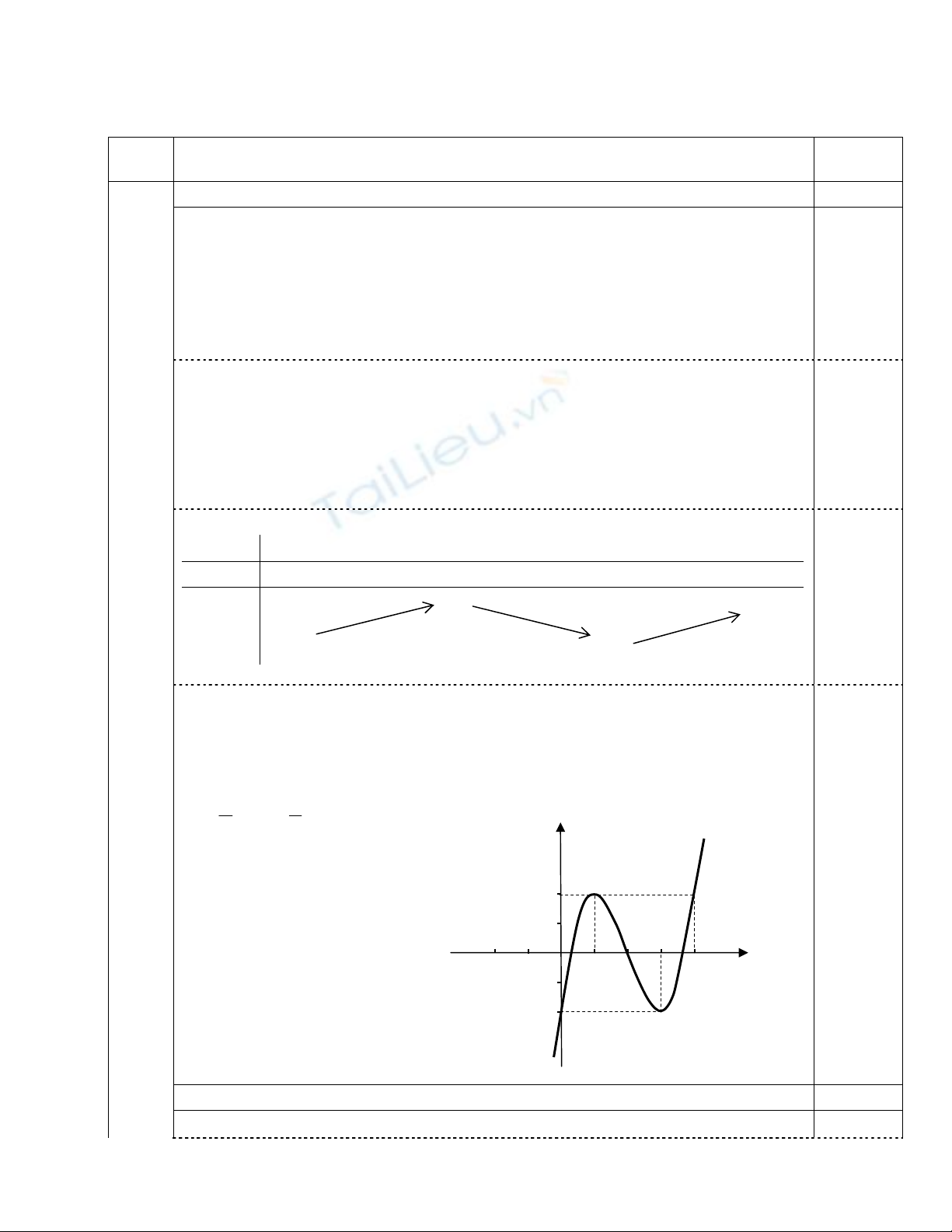
Cho hàm số: y = x3 – 6x2 + 9x – 2 có ñồ thị (C)
1) Khảo sát sự biến thiên và vẽ ñồ thị (C) của hàm số.
2) Tìm m ñể phương trình:
e3t – 2.e2t + ln3 + et + ln9 + m = 0 (1)
có 3 nghiệm phân biệt thuộc (–ln2; +∞).
Câu II (2 ñiểm).
Giải phương trình:
1) sinx(1+2cos2x) + 3cos3x = 2(cos4x + sin3x)
2)
4x
4x6
x224x2 2+
−
=−−+
Câu III. (1,0 ñiểm)
TÝnh I= dx
x
xx )
2
coscos1(
2
0
−+
∫
π
Câu IV. (1,0 ñiểm)
Cho hình lăng trụ ABC.A’B’C’ có ñáy ABC là tam giác ñều cạnh a,ñỉnh A’
cách ñều A,B,C và cạnh bên AA’ tạo với mặt phẳng (ABC) một góc 600. Gọi I là
trung ñiểm cạnh BC.
a) Tính thể tích khối lăng trụ ABC.A’B’C’ .
b) Tính khoảng cách giữa AI và BA’.
Câu V. (1,0 ñiểm)
Cho ba sè a, b, c sao cho
=
>
1
0,,
abc
cba
T×m gi¸ trÞ nhá nhÊt cña biÓu thøc A =
( )
2
bc
a b c
+
+
( )
2
ac
b a c
+
+
( )
2
ab
c b a
+
www.VNMATH.com
B. PHẦN RIÊNG (3,0 ñiểm) Thí sinh chỉ ñược làm một trong hai phần
(phần a, hoặc b).
a.Theo chương trình chuẩn:
C©u VI.a (2 ®iÓm)
1) Cho hai ®−êng trßn: (C1): x2+y2-2x-2y-2=0; (C2): x2+y2-8x-2y+16=0 .
Gäi I, K lÇn l−ît lµ t©m cña (C1) vµ (C2) ; M lµ ®iÓm tiÕp xóc gi÷a (C1) vµ (C2).
Gäi d lµ tiÕp tuyÕn chung kh«ng ®i qua M cña (C1) vµ (C2). d c¾t ®−êng th¼ng IK
t¹i A. LËp ph−¬ng tr×nh ®−êng trßn ®−êng kÝnh AM.
2)Trong kh«ng gian (Oxyz) cho hai ®iÓm A(0;0;-3); B(2;0;-1) và mặt cầu
(S) :(x-2)2+(y+1)2+z2=10. Hãy tìm trên (S) ñiểm C sao cho ABC là tam giác ñều.
C©u VII.a (1 ®iÓm)
Khai triển và rút gọn biểu thức :
( ) 1 2(1 ) ... (1 ) ,
n
P x x x n x n N
= − + − + + − ∈
thu ñược ña thức n
nxaxaaxP +++= ...)( 10 . Tính hệ số 8
a biết
n
thoả mãn:
n
CC nn
171
32 =+ .
b.Theo chương trình nâng cao:
Câu VIb. (2 ®iÓm)
1)Trong mặt phẳng với hệ toạ ñộ ,Oxy xét elíp )(E ñi qua ñiểm )3;2(
−
−
M và có
phương trình một ñường chuẩn là .08
=
+
x Viết phương trình chính tắc của ).(E
2)Trong không gian với hệ toạ ñộ ,Oxyz cho các ñiểm )2;3;0(),0;1;0(),0;0;1( CBA
và mặt phẳng .022:)(
=
+
+
yx
α
Tìm toạ ñộ của ñiểm
M
biết rằng
M
cách ñều
các ñiểm CBA ,, và mặt phẳng ).(
α
Câu VIIb. (1,0 ñiểm) Cho n là số tự nhiên, n
≥
2.Tính
2 2 1 2 2 2 2
1
2 1 . .2 2 . .2 ... . .2
n
k k n n
n n n n
k
S k C C C n C
=
= = + + +
∑
…………..Hết…………
www.VNMATH.com
1
ðáp án ðề thi thử ñại học khối A năm 2011
Câu ðáp án ðiểm
I 1 1 ñiểm
* Tập xác ñịnh: R
* Sự biến thiên
- Chiều biến thiên
y’ = 3x2 – 12x + 9
y’ = 0 ⇔ x = 1
hoặc x = 3
0,25
- Hàm ñồng biến trên mỗi khoảng (–∞; 1) và (3; +∞)
Hàm nghịch biến trên khoảng (1; 3)
- Cực trị: Hàm số ñạt tới cực ñại tại x = 1, ycñ = 2
Hàm số ñạt tới cực tiểu tại x = 3, yct = –2
- Giới hạn:
−∞
=
−∞→x
ylim ;
+∞
=
+∞→x
ylim
0,25
- Bảng biến thiên
x –∞ 1 3 +∞
y’ + 0 – 0 +
y
–∞
2
–2
+∞
0,25
* ðồ thị Tâm ñối xứng I(2; 0)
ðiểm phụ
x = 4 y = 2
x = 0, y = -2
x =
2
1 y =
8
9
x
0,25
2. 1 ñiểm
(1) ⇔ e3t – 6e2t + 9et + m = 0
2
-2
1 2 3 4
0
y
www.VNMATH.com
2
ðặt x = et > 0 ta ñược (1) trở thành
x3 – 6x2 + 9x + m = 0
⇔ x3 – 6x2 + 9x – 2 = – m – 2 (2)
0,25
Ta có phương trình (2) là phương trình hoành ñộ giao ñiểm của ñồ thị
(C) và ñường thẳng (d): y = –m – 2
⇒ số nghiệm của (2) chính là số giao ñiểm của (C) và d.
0,25
Mỗi nghiệm t ∈ (–ln2; +∞) của phương trình (1) cho một nghiệm x ∈
(
2
1; +∞) của phương trình (2) và ngược lại.
Do ñó (1) có 3 nghiệm phân biệt ∈ (–ln2; +∞)
⇔ (2) có 3 nghiệm x ∈ (
2
1; +∞)
0,25
(2) có 3 nghiệm x ∈ (
2
1; +∞) khi d cắt (C) tại 3 ñiểm có hoành ñộ
thuộc khoảng (
2
1; +∞) , f(
2
1) =
8
9
Dựa vào ñồ thị
8
9 < –m – 2 < 2
–4 < m < –
8
25
0,25
1. 1 ñiểm
Phương trình ⇔ sinx(1 – 2sin2x) + cosxsin2x + 3 cos3x = 2cos4x
⇔ sinxcos2x + cosxsin2x + 3 cos3x = 2cos4x
0,25
⇔ sin3x + 3 cos3x = 2cos4x 0,25
⇔
2
1sin3x +
2
3cos3x = cos4x
⇔ cos(3x –
6
π
) = cos4x
0,25
⇔ 3x –
6
π
= 4x + k2π x = –
6
π
+ k2π
3x –
6
π
= –4x + k2π x =
42
π
+ k
7
2
π
(k ∈ z)
0,25
2. 1 ñiểm
II
ðiều kiện –2 ≤ x ≤ 2
Phương trình ñã cho tương ñương với
(
)
(
)
4x
4x6
x224x2
x224x2x224x2
2+
−
=
−++
−++−−+
0,25
www.VNMATH.com
3
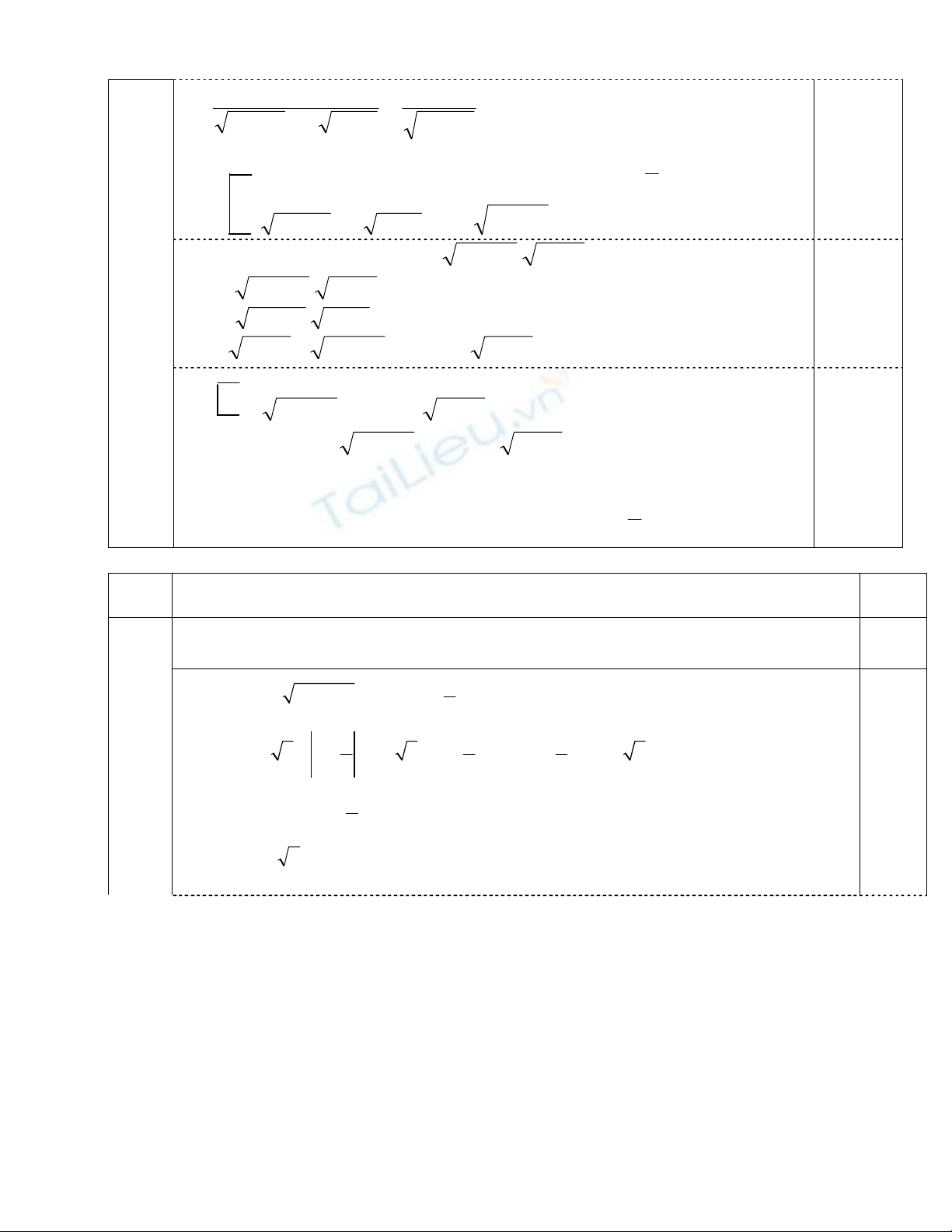
⇔ 4x
4x6
x224x2
4x6
2+
−
=
−++
−
⇔ 6x – 4 = 0 ⇒ x =
3
2
x
2
2
4
x
2
−++ =
4
x
2
+
(1)
0,25
(1) ⇔ 2x + 4 + 4(2 – x) + 4
(
)
x2.4x2 −+ = x2 + 4
⇔ 4
x
2
.
4
x
2
−
+
– ( x2 + 2x – 8) = 0
⇔ 4
x
2
.
4
x
2
−+ – ( x – 2) (x + 4) = 0
⇒
(
)
x2)4x(4x24x2 −+++− = 0
0,25
⇒ x =2
x2)4x(4x24 −+++ = 0
Với x ∈ [-2; 2]: x2)4x(4x24 −+++ > 0
⇒ x = 2
ðáp số: Phương trình có 2 nghiệm x =
3
2, x = 2
0,25
Câu ðáp án ðiểm
III 1 1
ñiểm
2 2
1 2
0 0
1 cos cos 2
x
I xdx x dx I I
π π
= + − = −
∫ ∫
2 2
1
0 0
2 cos 2( cos cos ) 4 2
2 2 2
x x x
I dx dx dx
π π π
π
= = − =
∫ ∫ ∫
∫−===
π
2
0
2
8...
2
sin2 x
xdI
824 +=I
0,25
0,25
0,25
0,25
www.VNMATH.com