SỞ GIÁO DỤC & ĐÀO TẠO BẮC NINH
TRƯỜNG THPT NGUYỄN ĐĂNG ĐẠO
ĐỀ THI THỬ ĐẠI HỌC LẦN 1
Năm học: 2013 – 2014
MÔN: TOÁN KHỐI A, B, A1, V
( Thời gian làm bài: 180 phút)
Câu 1 ( 2 Điểm): Cho hàm số: 3 2 2 3
y x m x x m
m
C
a, Khảo sát sự biến thiên và vẽ đồ thị hàm số với m = 0
b, Gọi A là điểm trên
m
C
và có hoành độ bằng -1. Tìm m để tiếp tuyến của (Cm) tại A song song với
đường thẳng d: y = 2x + 2.
Câu 2 ( 1 Điểm): Giải phương trình lượng giác:
2 cos 2 2 sin 3cossin x x x x
.
Câu 3 ( 1 Điểm): Giải hệ phương trình:
3 2 2
2
2 2
2 4 -12 - 1 0
x x y x y y y x y
x x y x y
Câu 4 ( 1 Điểm): Tìm m để phương trình sau có đúng 1 nghiệm x < 1:
21
m x mx
Câu 5 ( 1 Điểm): Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật, AB = 2AD = 2a. Mặt bên
SAB là tam giác vuông tại S và vuông góc với mp(ABCD). Góc giữa SA với mp(ABCD) bằng 600.
Gọi M là trung điểm của SC. Tính thể tích khối chóp S.ABCD và khoảng cách giữa SB và DM.
Câu 6 ( 1 Điểm): Cho
, ,x y z
là 3 số thực không âm thoả mãn: 2
1 1 2 1 2 5
x y z
.
Tìm giá trị lớn nhất của biểu thức:
3 3 3
2
P x y z
Câu 7 ( 1 Điểm): Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có diện tích bằng
. Các đỉnh A,
B, C lần lượt nằm trên các đường thẳng d1: x + y – 2 = 0; d2: 2x – y – 4 = 0; d3: x – y – 3 = 0. Gọi E,
F là 2 điểm lần lượt nằm trên các cạnh AB và AC sao cho AB = 3AE; AC = 3CF. Đường thẳng EF
cắt đường thẳng BC tại điểm P(-4; -8). Tìm toạ độ các đỉnh của tam giác ABC.
Câu 8 ( 1 Điểm): Trong mặt phẳng toạ độ Oxy, cho đường thẳng d: x – y = 0. Viết phương trình
đường tròn (C) qua điểm M(2; 0) và tiếp xúc với d tại O(0;0).
Câu 9 ( 1 Điểm): Cho khai triển: 2
0 1 2
3 ... .
2
n
n
n
x
a a x a x a x
Biết rằng: 0 1 2
2 4 ... 2 1024
n
n
a a a a . Tìm
6
a
.
……………….Hết……………….
( Cán bộ coi thi không giải thích gì thêm).
ĐÁP ÁN, THANG ĐIỂM THI THỬ ĐẠI HỌC LẦN 1
Năm học: 2013 – 2014
MÔN: TOÁN KHỐI A, B, A1, V
Câu Nội dung Điểm
1a Khảo sát và vẽ đồ thị: 3 2 2 3
y x m x x m
khi m = 0 1
Với m = 0, hàm số trở thành: y = x3 – 3x
TXĐ: D = R
lim
x
y


2
3 3
y x
1 2
0
1 2
x y
yx y
BBT:
x

-1 1

y’ + 0 - 0 +
y 2

-2

Hàm số đồng biến trên từng khoảng
; 1
và
1;

Hàm số nghịch biến trên ( -1; 1)
Đạt cực đại tại x = -1; yCĐ = 2
Đạt cực tiểu tại x = 1; yCT = -2
Đồ thị:
Giao Ox tại
3;0 ; 3;0 ; 0;0
f(x)=x^3-3*x
-8 -6 -4 -2 2 4 6 8
-5
5
x
y
0,25
0,25
0,25
0,25
1b Tìm m để tiếp tuyến tại điểm có hoành độ bằng -1 song song d: y = 2x + 2 1
Từ giả thiết ta có:
1 2
y
2
2 2 1
m m
Với m = 1
1;2M
pttt: y = 2x + 4 (thoả mãn)
Với m = -1
1;0M
pttt: y = 2x + 2 ( Loại)
Vậy: m = 1 là giá trị cần tìm
0,25
0,25
0,25
0,25
2 Giải pt:
sin 2 cos 2 2 sin 3cosx x x x
1
Phương trình tương đương: sinx(2cosx – 1) – (2cos2x – 3cosx + 1) = 0
sinx(2cosx – 1) – (2cosx – 1)(cosx – 1) = 0
(2cosx – 1)(sinx – cosx + 1) = 0
1
cos
2
sin cos 1
x
x x
*) 1
cos 2
2 3
x x k
*)
sinx cos 1 2 sin 1
4
x x
2
1
sin 3
4
2
22
x k
x
x k
Vậy pt có nghiệm:
2 ;
3
x k
2x k
; 3
2
2
x k
0,25
0,25
0,25
0,25
3 Giải hệ:
3 2 2
2
2 2 (1)
2 4 12 1 0 (2)
x x y x y y y x y
x x y x y
1
Đk:
0
y
Pt(1)
2
4
1 2
2 1 0
y x
x y x y
y x
*) Với y = 1 – 2x, thay vào (2) ta được:
0,25
2
0 1 ( / )
2 4 1 2 10 0
2 1 2 5 (*)
x y t m
x x x x x x
Pt(*)
2
5
4 1 2 5
x
x x
( Vô nghiệm)
*) Với y = x4 thay vào (2) ta được:
2x2 + 4x3 -12x – x4 + 1 = 0 432
4 2 12 1 0
x x x x
(**)
Đặt: x = t + 1
(**) thành: t4 – 8t2 + 6 = 0
4
4
4 10 1 4 10 1 4 10
4 10 1 4 10 1 4 10
t x y
t x y
Vậy hệ cho có nghiệm (x; y) = (0; 1);
4
1 4 10; 1 4 10
;
4
1 4 10; 1 4 10
0,25
0,25
0,25
4 Tìm m để phương trình: 21
m x mx
có đúng một nghiệm x < 1
1
Phương trình tương đương:
2
1 1
x m x
21
1
x
m
x
Xét hàm số:
2
1
1
x
f x
x
với x < 1
22
1
1 1
x
f x x x
0 1
f x x
;
lim ( ) 1
xf x

0,25
0,25
BBT:
x

-1 1
f x
+ 0 -
f x
1
2
-1

Từ bảng biến thiên ta thấy, phương trình cho có đúng 1 nghiệm x < 1 khi và chỉ
khi:
1
1
2
m
m
0,25
0,25
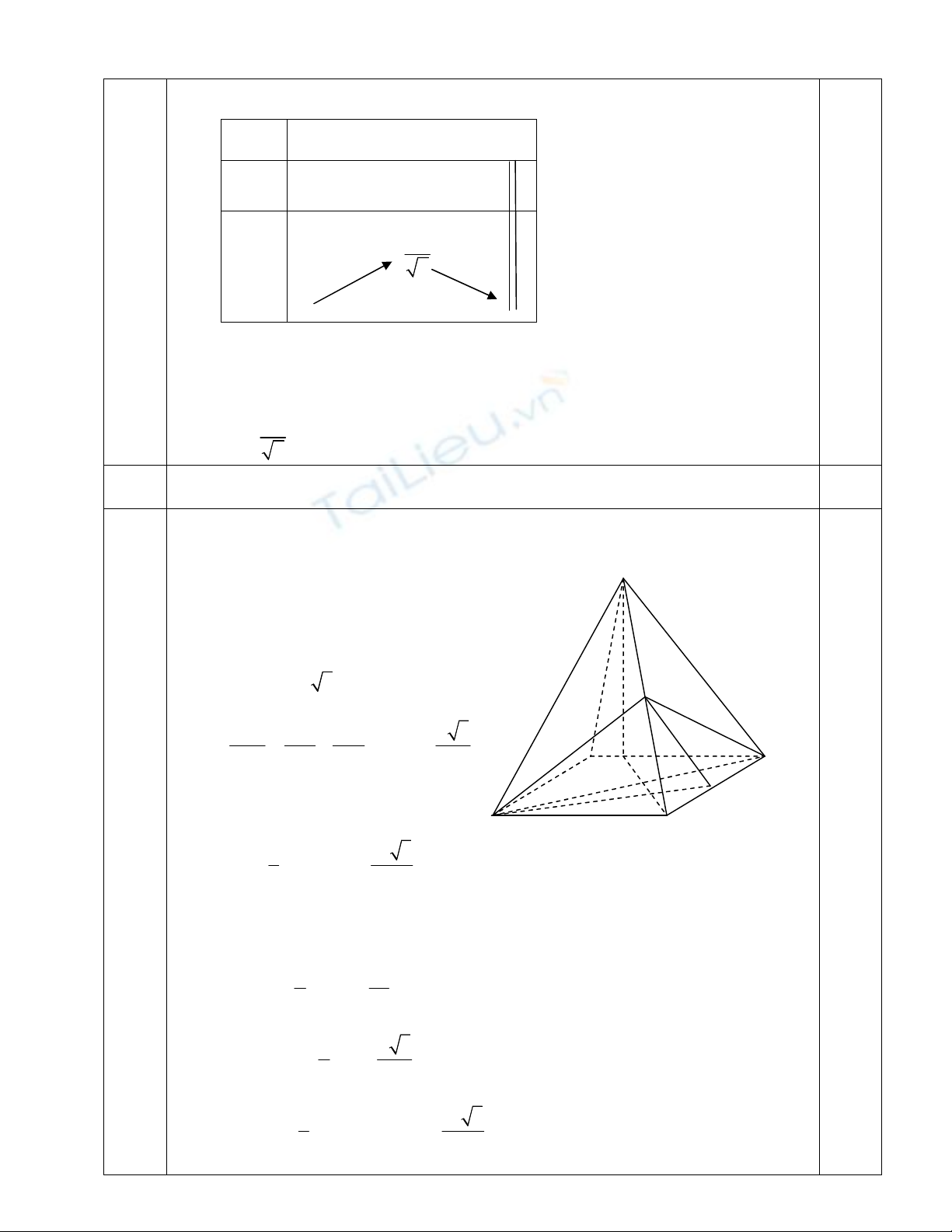
5 Hình học không gian
1
*) Hạ
SH AB
tại H
( )SH ABCD
Ta có:
0
;( ) 60
SA ABCD SAH
SAB
vuông tại S, có 0
60 ; 2SAB AB a
; 3SA a SB a
Ta có: 2 2 2
1 1 1 3
2
a
SH
SH SA SB
2
. 2
ABCD
S AB AD a
3
.
1 3
.
3 3
S ABCD ABCD
a
V SH S
*) Gọi N là trung điểm BC
SB//(DMN)
;;
SB DM
B DMN
d d
Ta có:
2
1
4 2
BDN ABCD
a
S S
;
1 3
2 4
M BDN
a
d SH
3
;( )
1 3
.
3 24
MBDN BDN
M BDN
a
V d S
0,25
0,25
0,25
S
A
B
C
D
H
M
N