TRƯỜNG THPT THỐNG NHẤT KỲ THI TỐT NGHIỆP THPT QUỐC GIA NĂM 2025
ĐỀ THAM KHẢO 01 Bài thi môn: TOÁN
(Đề gồm có 11 trang) Thời gian làm bài: 90 phút, không kể thời gian phát đề
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi
câu hỏi thí sinh chỈ chọn một phương án.
Câu 1: Nguyên hàm của hàm số là:
A. .B. .C. .D. .
Lời giải
Chọn C
Ta có :
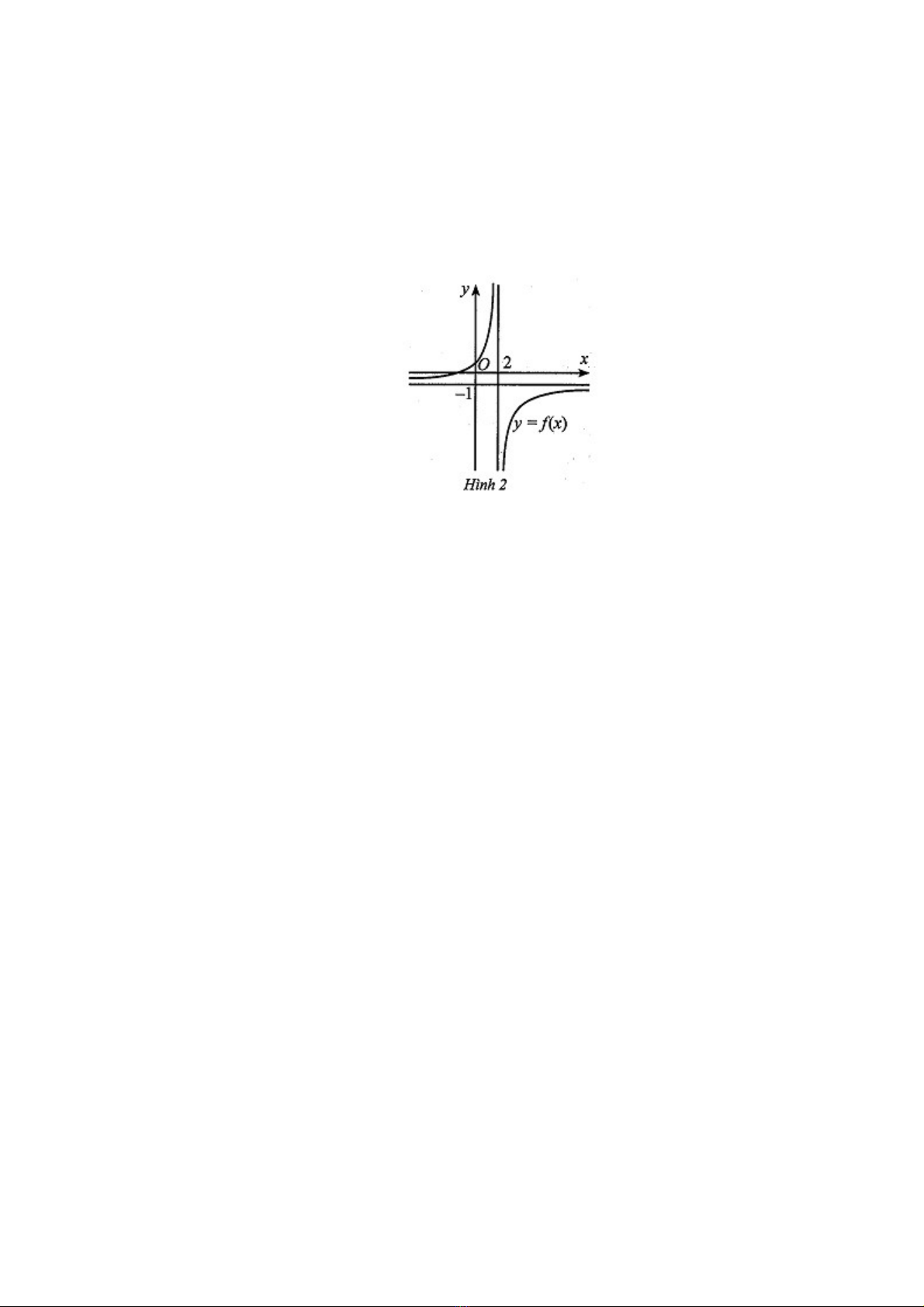
Câu 2: Cho hàm số liên tục, không âm trên đoạn như hình 3.
Hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng ; quay quanh trục
tạo thành một khối tròn xoay có thể tích bằng
A. . B. . C. .D. .
Lời giải
Chọn D. Ta có :
Câu 3: Xét mẫu số liệu ghép nhóm cho bởi Bảng 1. Số trung bình cộng của mẫu số liệu ghép
nhóm đó bằng
Nhóm Giá trị đại
diện
Tần số
Bảng 1
A. .B. .
C. .D. .
Lời giải
Chọn D
Câu 4: Trong không gian tọa độ phương trình nào sau đây là phương trình tham số của đường
thẳng?
A. B. C. D.
Lời giải
Chọn D
Ta thấy là một phương trình tham số của đường thẳng.
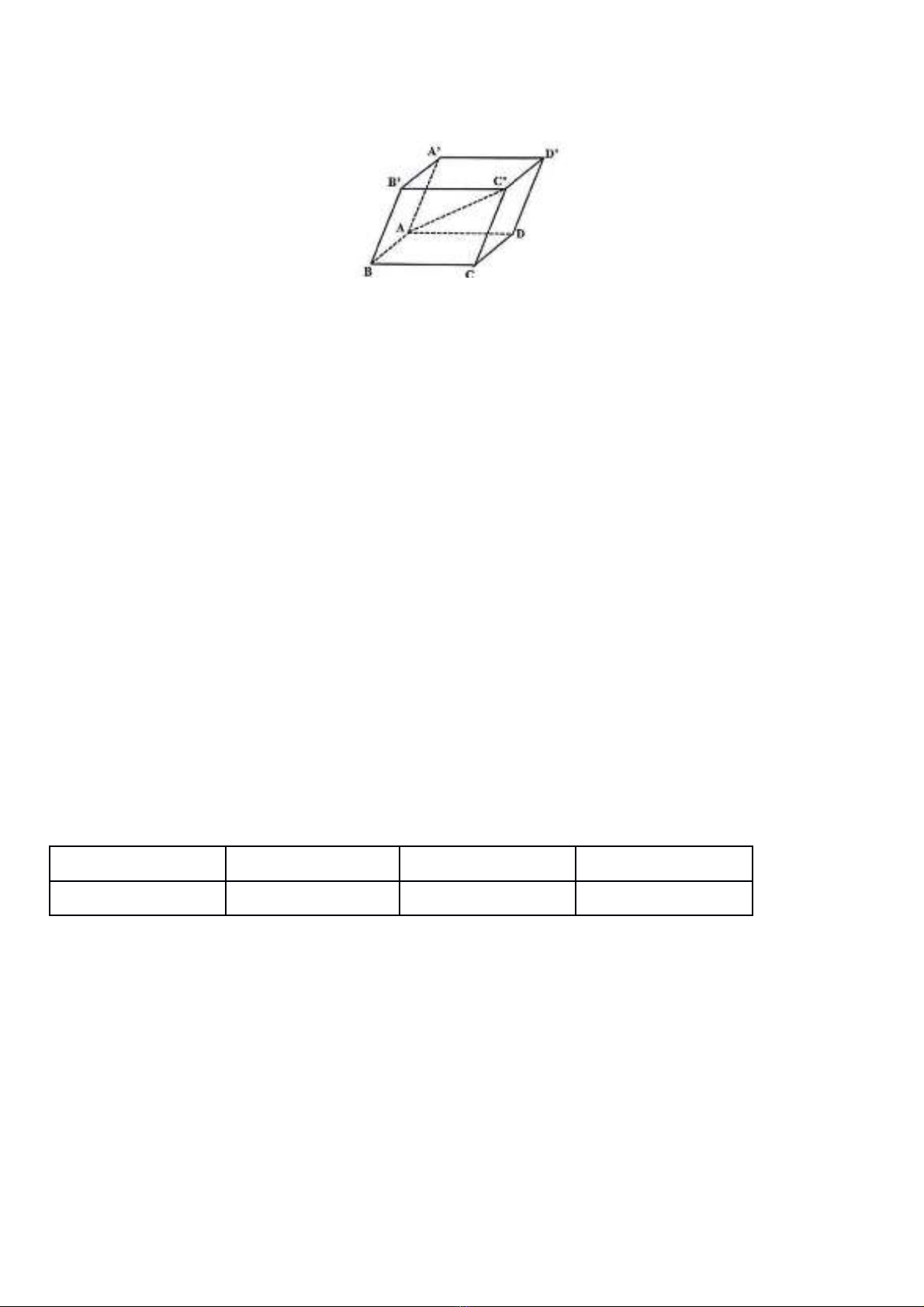
Câu 5: Cho haIm sôJ coJ đôI thiK như Hi%nh 2.
Phương triInh đươIng tiêKm câKn đưJng cuMa đôI thiK haIm sôJ laI:
A. .B. .C. .D. .
Lời giải
Chọn B
Câu 6: Tập nghiệm của bất phương trình là:
A. .B. .C. .D. .
Lời giải
Chọn C
Ta có
Câu 7: Trong không gian , đường thẳng có một vectơ chỉ phương là:
A. . B. . C. . D. .
Lời giải
Chọn B
Một vécto chỉ phương của đường thẳng là .
Câu 8: Cho hình hộp chữ nhật . Chọn phát biểu sai trong các phát biểu sau ?
A. .B. .C. .D. .
Lời giải
Chọn A
Câu 9: Tìm nghiệm của phương trình .
A. 3. B. 1C. 4D. 2
Lời giải
Chọn A.
Câu 10: Cho cấp số nhân có , . Tính công bội ?
A. 5. B. 7. C. 9. D. 4.
Lời giải
Chọn D.
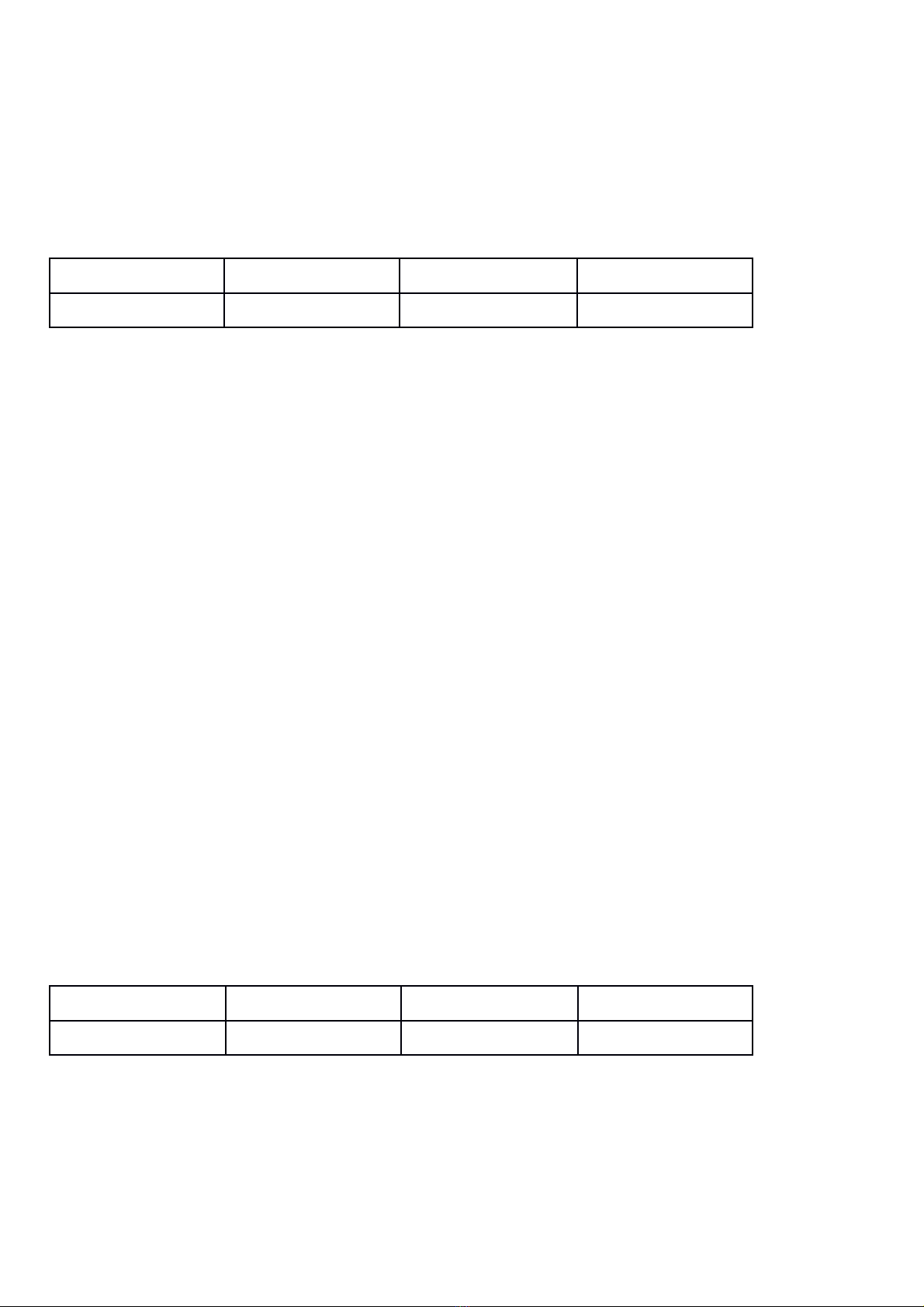
Câu 11: Cho hình hộp (minh họa như hình bên). Phát biểu nào sau đây là sai ?
A. .B. .
C. .D. .
Lời giải
Chọn C
Câu 12: Cho hàm số có đồ thị như hình vẽ. Hàm số nghịch biến trong khoảng nào?
A. .B. .C. .D. .
Lời giải
Chọn D
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d)
ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho hàm số .
a) .
b) Đạo hàm của hàm số đã cho là .
c) Nghiệm của phương trình trên đoạn là hoặc .
d) Giá trị nhỏ nhất của trên đoạn là .
Đáp án
a) b) c) d)
Đúng Sai Đúng Đúng
a) .
b) Đạo hàm của hàm số là .
c)
d)
Giá trị nhỏ nhất của trên đoạn là .
Câu 2: Một công ty đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là và khả năng thắng thầu
của dự án 2 là . Khả năng thắng thầu cả 2 dự án là .
Gọi là biến cố: “Thắng thầu dự án 1”
Gọi là biến cố: “Thắng thầu dự án 2”.
Khi đó:
a) và là hai biến cố độc lập.
b) Xác suất để công ty thắng thầu đúng 1 dự án bằng .
c) Xác suất để công ty thắng thầu dự án 2 biết công ty thắng thầu dự án 1 là .
d) Xác suất để công ty thắng thầu dự án 2 biết công ty không thắng thầu dự án 1 là .
Đáp án
a) b) c) d)
Sai Sai Đúng Sai
a) và là hai biến cố độc lập
Mà nên không độc lập
b) Gọi là biến cố “ thắng thầu đúng một dự án”
c) Gọi là biến cố “ thắng dự án 2 biết thắng dự án 1”
d) Gọi là biến cố “ thắng dự án 2 biết không thắng dự án 1”
Câu 3: Một xe ô tô đang chạy với vận tốc thì người lái xe bất ngờ phát hiện chướng ngại vật trên
đường cách đó . Người lái xe phản ứng một giây, sau đó đạp phanh khẩn cấp. Kể từ thời
điểm này, ô tô chuyển động chậm dần đều với tốc độ , trong đó là thời gian tính bằng giây
kể từ lúc đạp phanh. Gọi là quảng đường xe ô tô đi được trong (giây) kể từ lúc đạp
phanh.
a) Quảng đường mà xe ô tô đi được trong thời gian (giây) là một nguyên hàm của hàm
số .
b) .
c) Thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là giây.
d) Xe ô tô đó không va vào chướng ngại vật ở trên đường.
Đáp án
a) b) c) d)
Đúng Đúng Sai Đúng
a) Do nên quãng đường mà xe ô tô đi được trong thời gian (giây) là một nguyên
hàm của hàm số .
b) Ta có: với là hằng số.
Do nên . Suy ra .
c) Xe ô tô dừng hẳn khi hay . Vậy thời gian kể từ lúc đạp phanh
đến khi xe ô tô dừng hẳn là 2 giây.
d) Ta có xe ô tô đang chạy với tốc độ .
Do đó, quãng đường xe ô tô còn di chuyển được kể từ lúc đạp phanh đến khi xe dừng hẳn
là: .
Vậy quãng đường xe ô tô đã di chuyển kể từ lúc người lái xe phát hiện chướng ngại vật
trên đường đến khi xe ô tô dừng hẳn là: .
Do nên xe ô tô đã dừng hẳn trước khi va chạm với chướng ngại vật trên đường.
Câu 4: Trong không gian với hệ tọa độ Oxyz, một cabin cáp treo xuất phát từ điểm và chuyển
động đều theo đường cáp có véc tơ chỉ phương (hướng chuyển động cùng chiều với
hướng véc tơ với tốc độ là (đơn vị trên mỗi trục là mét).
a) Phương trình tham số của đường cáp là:
b) Giả sử sau thời gian t (s) kể từ khi xuất phát (), cabin đến điểm M. Khi đó tọa độ điểm
M là ).
c) Cabin dừng ở điểm B có hoành độ , khi đó quãng đường AB dài 800m.
d) Đường cáp AB tạo với mặt phẳng một góc .
Đáp án
a) b) c) d)
Đúng Đúng Sai Sai
a) Đường cáp treo qua và có vectơ chỉ phương
Phương trình tham số của đường cáp là:
b) Đường cáp treo có vectơ chỉ phương nên nhận làm vectơ chỉ phương, M thuộc
đường cáp treo do đó tọa độ điểm M là ).
c) Giả sử B)
Ta có
d) VTPT cỏ (Oxy) là ,
Phần III. Câu hỏi trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
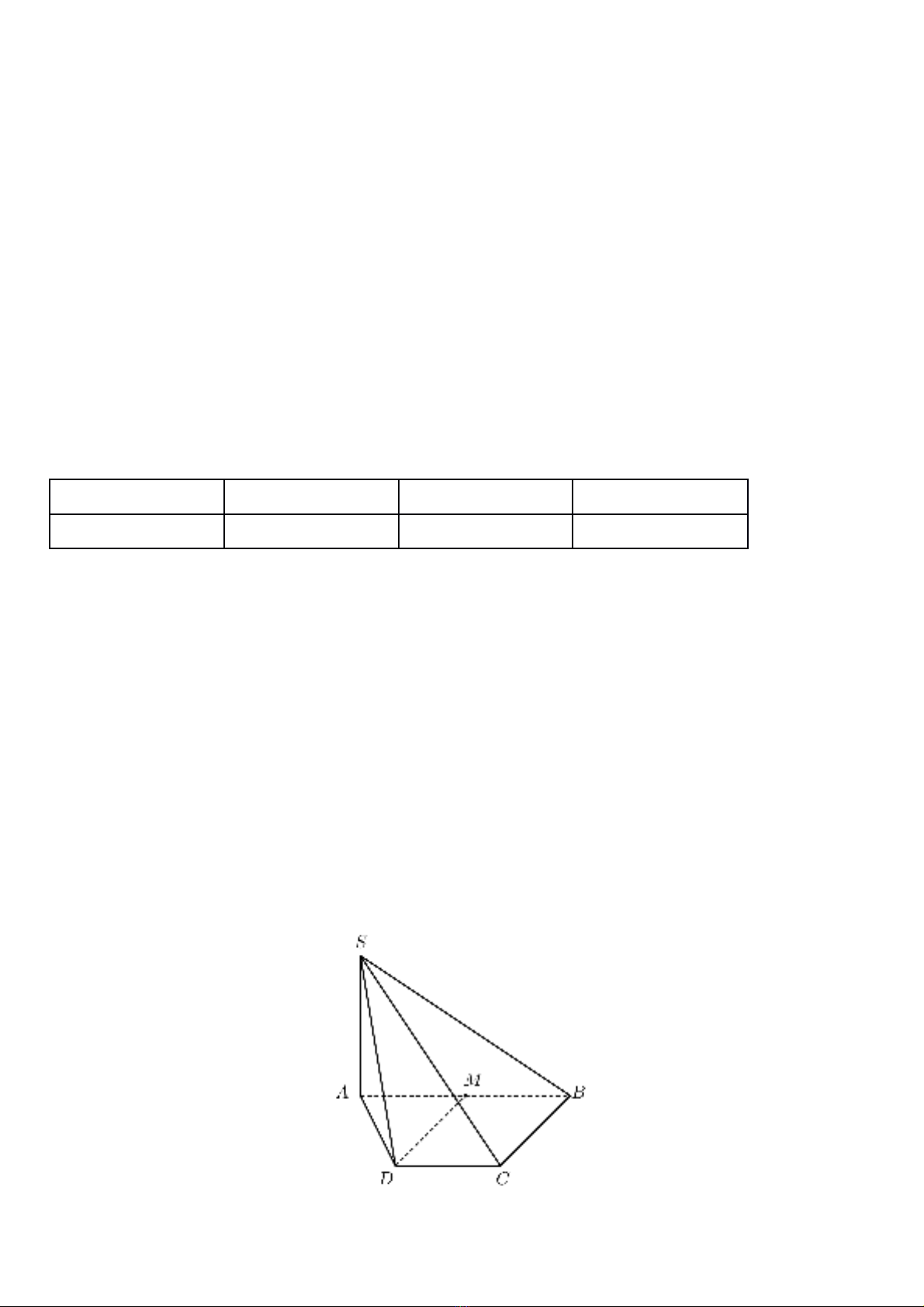
Câu 1: Cho hình chóp có đáy là hình thang,. Đường thẳng SA vuông góc với mặt phẳng đáy và
(minh họa như hình bên). Gọi là trung điểm của . Khoảng cách giữa hai đường thẳng SB
và DM bằng ?
Lời giải
Đáp số: 0,75.