1
SỞ GD&ĐT QUẢNG NAM
TRƯỜNG THPT ĐỖ ĐĂNG TUYỂN
ĐỀ ÔN TẬP THI TỐT NGHIỆP THPT NĂM 2014
MÔN TÓAN (Thời gian làm bài: 150 phút)
A/ PHẦN CHUNG DÀNH CHO TẤT CẢ THÍ SINH (7.0 điểm):
Câu I (3,0 điểm ):Cho hàm số 42
yx 2x 1=− −
có đồ thị (C).
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
b) Dựa vào đồ thị (C) tìm tất cả các giá trị của tham số m để phưong trình 42
x2xm0−−=
có nhiều hơn hai nghiệm phân biệt.
Câu II (3,0 điểm):
a)Giải phương trình : log4(2x2 + 8x) = log2x + 1 . b)Tính
2
4
0
sin .
I
xdx
π
=∫
c)Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
x
e
yx
ee
=
+
trên đoạn [ln2;ln4] .
Câu III (1,0 điểm):Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cà các cạnh đều bằng
a.Tính thể tích của khối lăng trụ và diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a .
B/ PHẦN RIÊNG( 3 điểm): Thí sinh chỉ được chọn làm một trong 2 phần sau ( phần I
hoặc phần II):
PhầnI (Theo chương trình chuẩn):
Câu IVa (2,0 điểm): Trong không gian Oxyz cho M (1; 2 ;-2), N (2; 0; -1) và mặt phẳng
( P) : 3210xy z++ −=.
a).Viết phương trình mặt phẳng ( Q ) qua 2 điểm M; N và vuông góc với ( P ).
b).Viết phương trình mặt cầu ( S ) tâm I ( -1; 3; 2 ) và tiếp xúc mặt phẳng ( P ).
Câu Va (1 điểm).Tính diện tích hình phẳng giới hạn bởi đồ thị (C) của hàm số
2
yx(x1)=− và tiếp tuyến của (C) tại gốc tọa độ O.
PhầnII (Theo chương trình nâng cao):
Câu IVb: ( 2,0 điểm ) Trong không gian với hệ toạ độ Oxyz, cho 2 đường thẳng:
Δ1: 3
1
2
1
1
2
−
−
=
+
=
−z
y
x , Δ2:
xt
y2t
z12t
=
⎧
⎪=−
⎨
⎪=+
⎩
và mặt cầu (S): x2 + y2 + z2 – 2x + 4y – 6z – 2 = 0.
a) Chứng minh Δ1, Δ2 chéo nhau và tính khoảng cách giữa hai đường thẳng đó.
b)) Viết phương trình mặt phẳng (α) song song với hai đường thẳng Δ1, Δ2 và cắt mặt cầu
(S) theo giao tuyến là đường tròn (C) có chu vi bằng 8π.
Câu Vb(1,0 điểm): Chứng minh rằng tích các khoảng cách từ một điểm bất kỳ trên đồ thị (C ) của
hàm số 1
yx
x
=+ đến hai tiệm cận của nó là một hằng số.
------------------------ Hết -------------------------
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ tên thí sinh:........................................ Số báo danh:..................................
Chữ ký của giám thị 1:............................ Chữ ký của giám thị 2:.................
2
Trường THPT ĐỖ ĐĂNG TUYỂN
ĐÁP ÁN ĐỀ ÔN TẬP THI TỐT NGHIỆP THPT 2011, MÔN TOÁN
Câu Đáp án Điểm
Câu I
(3 điểm)
1) (2 điểm)
a) Tập xác định: D = R
0,25
b) Sự biến thiên:
+ Giới hạn : x
lim
→+∞ =+∞, x
lim
→−∞
=
+∞
+ Lập bảng biến thiên của hàm số :
y’ =
32
444(1)xxxx−= − ; 0
'0 1
x
yx
=
⎡
=⇔
⎢
=
±
⎣
Bảng biến thiên:
x –∞ -1 0 1 +
∞
y’ – 0 + 0 – 0 +
y +∞ -1 +
∞
–2 -2
Hàm số đồng biến trên mỗi khoảng (-1 ;0), (1 ;+∞) nghịch biến
trên mỗi khoảng (–∞ ;-1), (0 ;1). Đạt cực tiểu tại 1x
=
±, giá trị cực
tiểu: (1) 2y±=−, đạt cực đại tại x = 0, giá trị cực đại: y(0)= -1.
0,25
0,25
0,5
0,25
c) Đồ thị:
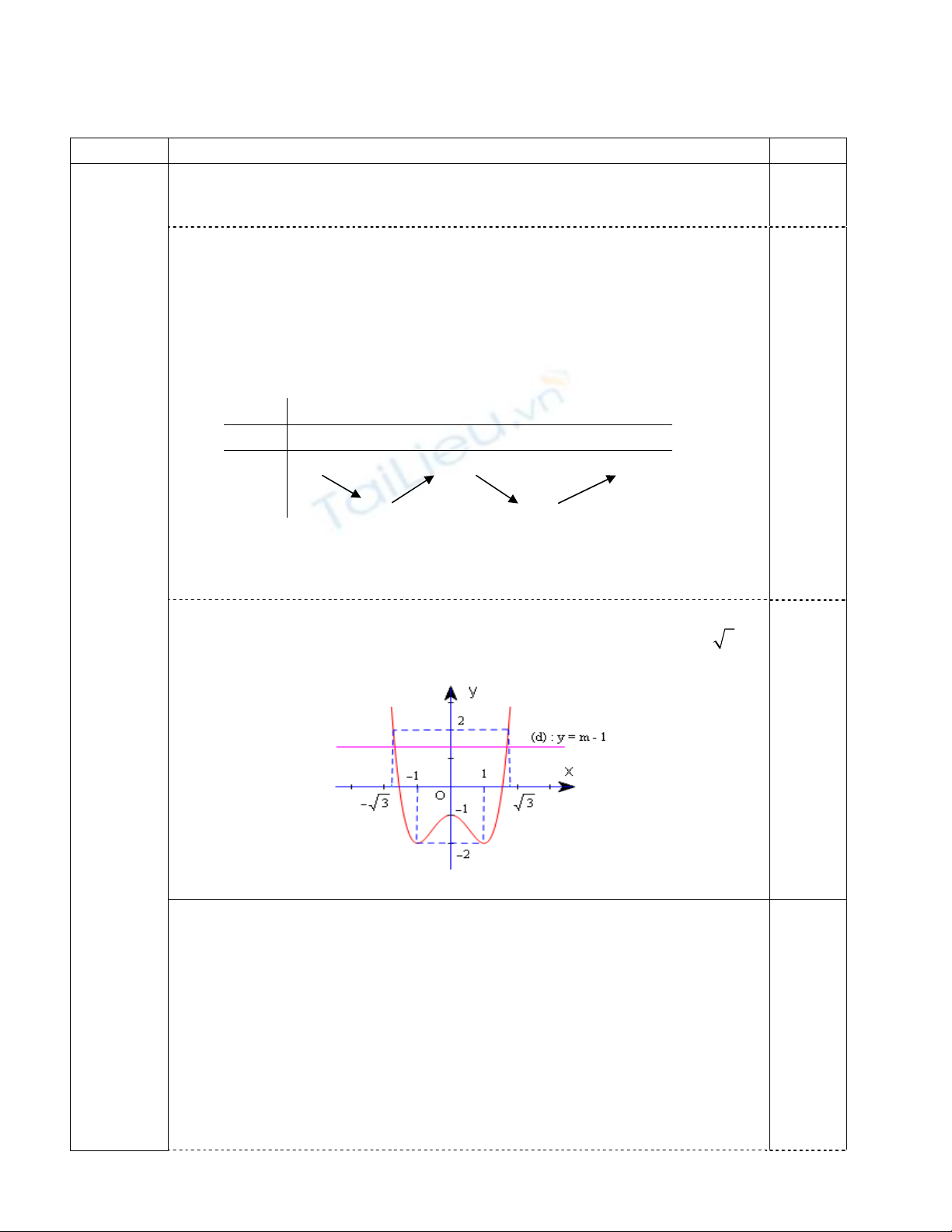
Giao điểm của đồ thị với các trục tung: (0;–1), đồ thị qua (3;2)m
Vẽ đồ thị:
Đồ thị nhận Oy làm trục đối xứng:
0,5
2) (1điểm)
+ Phương trình đã cho tương đương với:
42
21 1xx m−−=− (1)
+Số nghiệm của phương trình (1) bằng số giao điểm của đồ thị (C)
và đường thẳng (d): y = m – 1
+Phương trình đã cho có nhiều hơn 2 nghiệm phân biệt khi và chỉ
khi đường thẳng (d) cắt đồ thị (C) tại 3 hoặc 4 điểm phân biệt.
+Dựa vào đồ thị chọn: –2 < m – 1
≤
-1
hay: -1 < m
0
0,25
0,25
0,25
0,25
3
Câu II
(3 điểm)
1) (1 điểm) Giải phương trình: log4(2x2 + 8x) = log2x + 1 (1)
Điều kiện: x > 0.
Khi đó: (1)
⇔ log4(2x2 + 8x) = log4(4x2)
⇔ 2x2 + 8x = 4x2
⇔ x2 – 4x = 0 ⇔ x = 0 hoặc x = 4.
Kết hợp với điều kiện x > 0 suy ra PT (1) có một nghiệm: x=4.
0,25
0,25
0,25
0,25
2) (1 điểm)
+Đặt 22txxtdxtdt=⇒=⇒= ,
2
00;
42
xtx t
π
π
=
⇒= = ⇒=
+
2
0
2.sin
I
ttdt
π
=∫
+Đặt tptp u, dv suy ra du, v đúng.
+Kết quả I = 2
0,25
0,25
0,25
0,25
Câu II
3) (1 điểm)
+
1
2
'()
x
x
e
yee
+
=+
+
[
]
' 0, ln2;ln4yx>∀∈ nên hàm số đồng biến trên
[
]
ln 2;ln 4
+min
2
(ln 2) 2
yy e
==
+
+ max
4
(ln 4) 4
yy e
==
+
0,25
0,25
0,25
0,25
Câu III
(1 điểm)
+ Hình vẽ: Gọi O, O’ lần lượt là tâm các
đường tròn ngoại tiếp ;'''ABC A B CΔΔ thì
tâm của mặt cầu là trung điểm I của OO’
+ Tính được
33
4
lt
a
V=
+ Tính được 21
6
a
R=
+ Tính được
2
7
3
mc
a
S
π
=
0,25
0,25
0,25
0,25
Câu IV.a
(2 điểm)
1) (1 điểm)
+ (1; 2;1)MN =−
uuuur
, (3;1; 2)
P
n=
uur
+ ;(5;1;7)
QP
nMNn
⎡⎤
⇒= =−
⎣⎦
uur uuuuruur
+ Pt mp(Q): -5(x-1) + 1(y-2) + 7(z+2) = 0
+ Kết quả: 5x – y – 7z – 17 = 0.
0,25
0,25
0,25
0,25
4
2) (1 điểm)
+ R = d(I ;(P))
= 3
14
+ Pt (S) : 222
9
(1)( 3)(2)14
xyz++−+− =
0,25
0,25
0,5
Câu V.a
(1 điểm)
+ Lập được pttt tại gốc tọa độ O: y = x
+ Giải pt hoành độ tìm được 2 cận: 0; 2.xx
=
=
+
2
32
0
2Sxxxxdx=−+−
∫
+ Kết quả: 4
3
S=
0,25
0,25
0.25
0.25
Câu Đáp án Điểm
Câu IV.b
(2 điểm)
1) (1 điểm)
+ Δ1 qua M1(2 ; –1 ; 1) và có vectơ chỉ phương 1
u
u
ur
= (1 ; 2 ; –3).
Δ2 qua M2(0 ; 2 ; 1) và có vectơ chỉ phương 2
u
u
ur
= (1 ; – 1 ; 2).
+ [ 1
u
uur
, 2
u
uur
] = (1 ; –5 ; –3). M1M2 = (–2 ; 3 ; 0)
+ [ 1
u
uur
, 2
u
uur
]12
MM
uuuuuur
= –17 ≠ 0 => Δ1 và Δ2 chéo nhau.
+ Tính được: d(Δ1 ; Δ2 ) = 17
35
0,25
0,25
0,25
0,25
2) (1 điểm)
+ Mặt cầu (S) có tâm I(1; –2 ; 3) và bán kính R = 4.
+ Mặt phẳng (α) song song với Δ1 , Δ2 nên có vectơ pháp tuyến:
12
n[u,u]=
ruuruur
= (1;– 5; – 3).
+ Gọi r là bán kính đường tròn (C), ta có: 2πr = 8π
=> r = 4 => r = R => I ∈ (α)
+ Phương trình mặt phẳng (α): x – 5y – 3z – 2 = 0.
Vì M1 và M2 không thuộc (α) nên Δ1 // (α) và Δ2 // (α).
Vậy phương trình mặt phẳng (α) cần tìm là: x – 5y – 3z – 2 = 0.
0,25
0,25
0,25
0,25
Câu V.b
(1 điểm)
+ Lý luận tìm được TCĐ: x = 0 (d) ; TCX: y = x (d’)
+1
() (; ) ( 0)MC Mtt t
t
∈⇒ + ≠ (;)dMd t⇒=
+ 1
(;') 2
dMd t
=
+ Suy ra: 2
(;).(;') 2
dMd dMd =(đpcm).
0,25
0,25
0,25
0.25