
MA TRẬN ĐỀ THI TUYỂN SINH 10 CHUYÊN MÔN TOÁN
THỜI GIAN LÀM BÀI 150 PHÚT
TT
Nội
dung
kiến
thức
Đơn
vị
kiến
thức
Mức
độ
nhận
thức
Tổng %
Nh
ận
biết
Thôn
g hiểu Vận dụng Vận dụng
cao
Số
câu
hỏi
Thời
gian
(phút)
Số
câu
hỏi
Thời
gian
(phút
)
Số
câu
hỏi
Thời
gian
(phút
)
Số
câu
hỏi
Thời
gian
(phút
)
Số
câu
hỏi
Thời
gian
(phút
)
1
Căn
bậc
hai.
Hệ
phươ
ng
trình
1.Tí
nh
giá
trị
biểu
thức,
liên
quan
đến
CBH.
1 7 2 20
20%
2.Hệ
PT 1 13
2Đa
thức.
Bất
đẳng
thức
1. Đa
thức 1 10 2 25
20%
2.Bất
đẳng
thức 1 15
3
Số
học
1.Số
nguy
ên tố
1 13 2 25
15%
2.PT
nghiệ
m
nguy
ên
1 12
4
Hình
học
phẳn
g
Hình
học
phẳn
g
1 10 2 40 3 50 30%
5
Toán
rời
rạc,
Xác
suất
1.Ng
uyên
lí
Diric
hle
2 15 2 30
15%
2.Xá
c
suất.
1 15 1
Tổng 4 40 8 110 12 150 100%
Tỉ lệ % 40% 60% 100
%
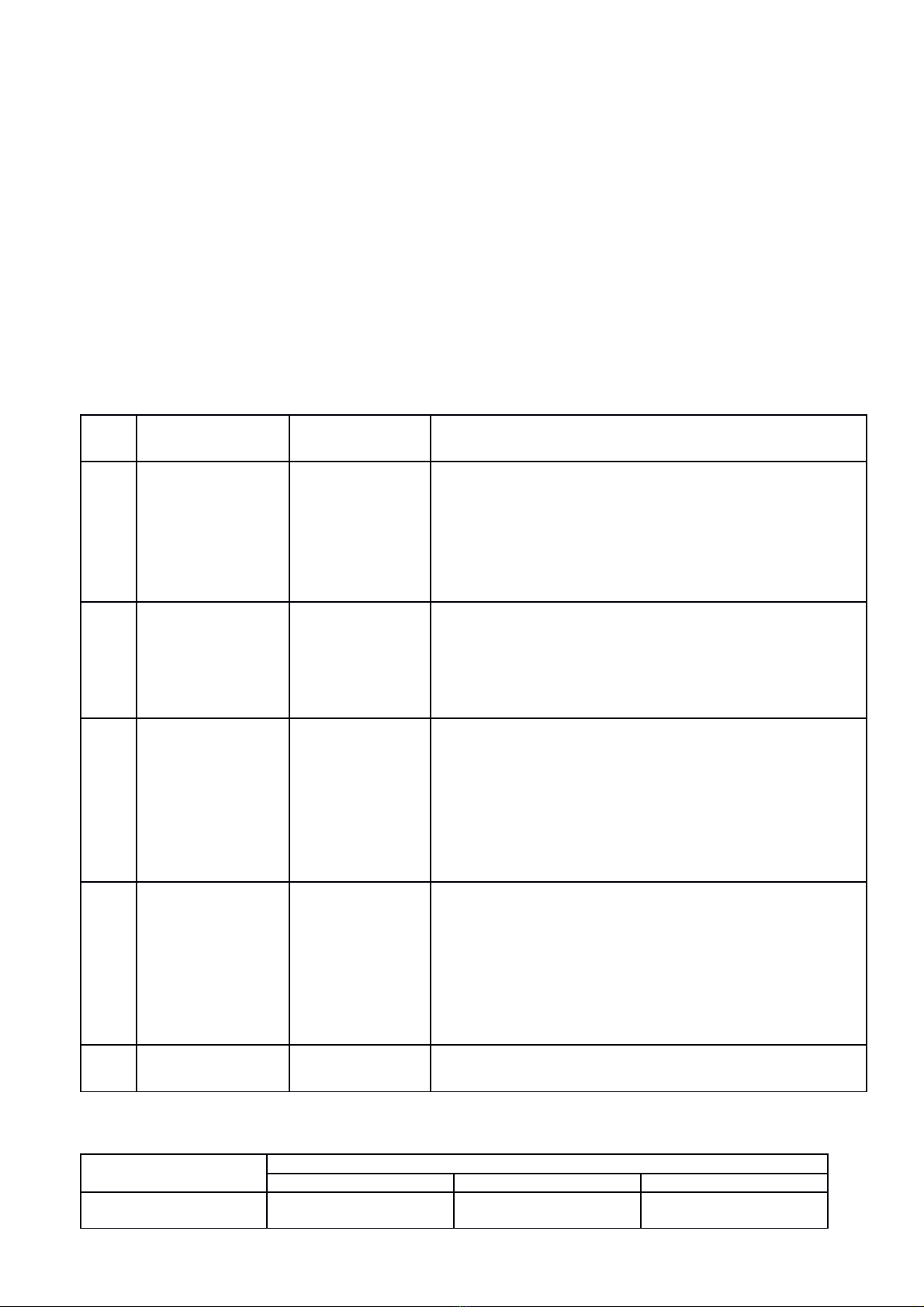
BẢN ĐẶC TẢ ĐỀ THI
câu Nội dung kiến
thức
Đơn vị kiến
thức
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh
giá
1
Căn bậc hai.
Hệ phương trình
-Tính giá trị
biểu thức.
- Hệ phương
trình không
mẫu mực
- Kĩ năng phân tích thành nhân tử, phối hợp các
phép biến đổi đồng nhất biểu thức chứa căn bậc
hai.
- Kỹ năng dùng hằng đẳng thức biến đổi 1 trong hai
PT của hệ PT thành dạng luỹ thừa cùng bậc ở 2 vế,
sử dụng phương pháp thế.
2- Đa thức.
- Bất đẳng thức
- Đa thức với
hệ số nguyên.
- Tìm GTNN
của biểu thức
có ĐK.
- Sử dụng hệ quả định lí Bơdu. Kĩ năng biến đổi đại
số các đa thức một biến.
- Kĩ năng tách hạng tử để có thể áp dụng BĐT quen
thuộc, ngoài ra kết hợp vận dụng BĐT Cauchy.
3Số học
- Chứng minh
bài toán liên
quan đến số
nguyên tố.
- Giải PT
nghiệm tự
nhiên.
Vận dụng tính chất:
đồng thời sử dụng định lý Fermat nhỏ.
Kĩ năng sử dụng linh hoạt các tính chất chia hết
trong tập hợp số nguyên.
4Hình học phẳng. Hình học
phẳng.
-Vận dụng hệ thức lượng trong tam giác, trong
đường tròn.
-Vận dụng t/c góc nội tiếp, tỉ số lượng giác, t/c hình
bình hành, tam giác cân, tam giác bằng nhau, quỹ
tích…vào việc chứng minh sự bằng nhau, hệ thức
hình học. Dùng định lý Ptolemy.
- Chứng minh điểm thuộc đường cố định.
5Toán rời rạc,
Xác suất.
-Suy luận logic
-Tính xác suất
Phân chia trường hợp và suy luận logic.
Tính xác suất của một biến cố.
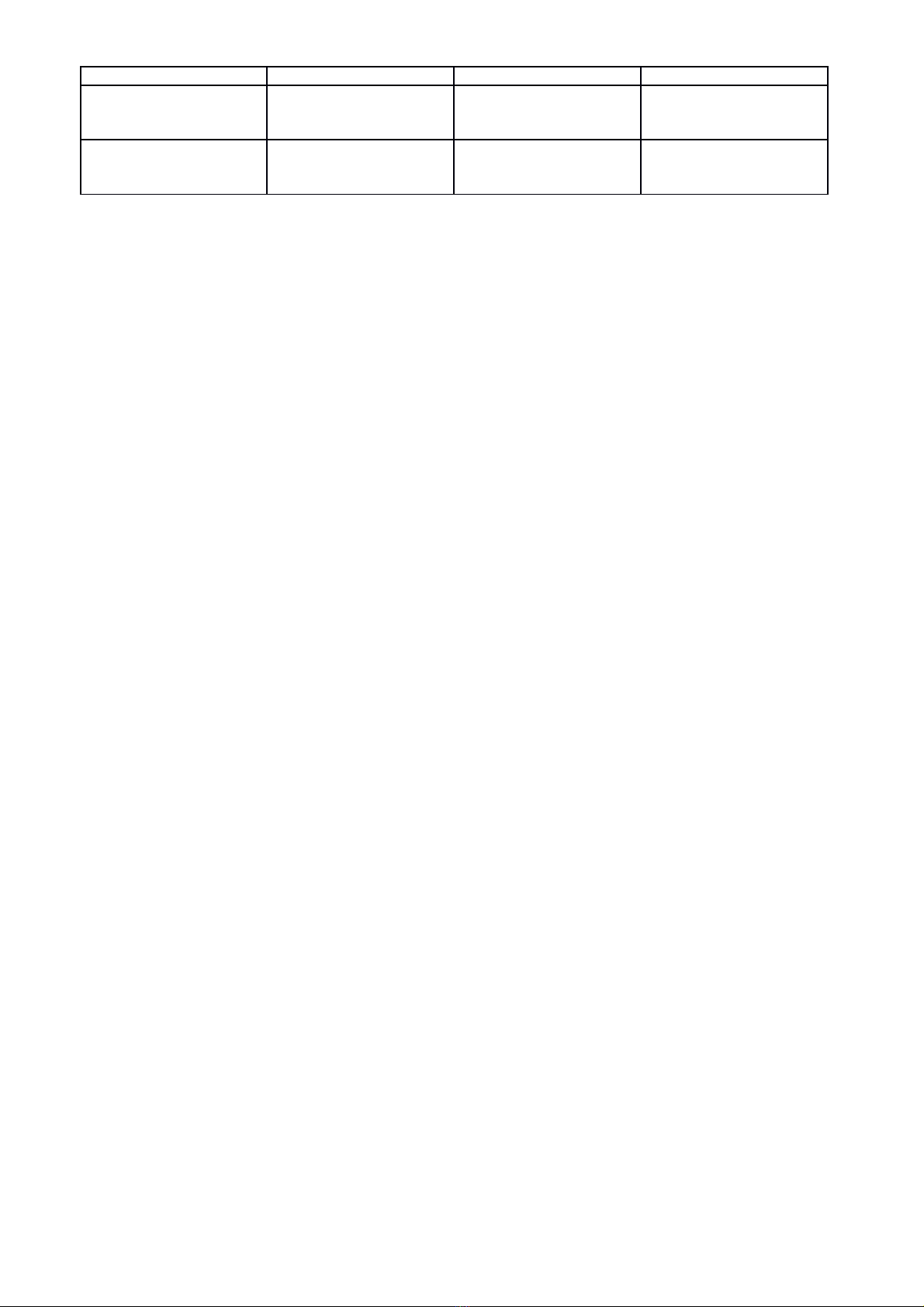
BẢNG NĂNG LỰC VÀ CẤP ĐỘ TƯ DUY
Năng lực Cấp độ tư duy
Thông hiểu Vận dụng Vận dụng cao
Tư duy và suy luận toán
học
Câu 1.1 Câu 1.2
Câu 2.1
Câu 2.2
Câu 3.1
Câu 4 (a) Câu 4(b) Câu 4 (c)
Giải quyết vấn đề toán học Câu 5.2 Câu 3.2 Câu 5.1 (a,b)
Tổng
(số lệnh hỏi và cấp độ tư
duy)
3 4 5
PHÒNG GIÁO DỤC VÀ
ĐÀO TẠO T.P TAM ĐIỆP
Trường THCS Đồng giao
ĐỀ THI TUYỂN SINH VÀO LỚP 10 CHUYÊN
Năm 2025
MÔN: TOÁN
Thời gian làm bài 150 phút
(Đề thi gồm 05 câu trong 01 trang)
Câu 1 (2 điểm).
1) Cho đa thức với biết. Tính giá trị của
2) Giải hệ phương trình .
Câu 2 (2 điểm).
1) Biết và số dư trong phép chia đa thức cho bằng 17. Chứng minh rằng giá trị của đa
thức Q tại là một số nguyên tố.
2) Cho . Tìm giá trị nhỏ nhất của biểu thức:
Câu 3 (1,5 điểm).
1) Cho . Chứng minh rằng mọi ước nguyên tố của đều có dạng (với , là số nguyên tố
lẻ).
2) Tìm tất cả các cặp số nguyên dương thỏa mãn.
Câu 4 (3 điểm). Cho tam giác có ba góc nhọn, . Các đường cao của tam giác cắt nhau tại
điểm . Gọi là đường tròn ngoại tiếp tứ giác , trên cung nhỏ của đường tròn lấy điểm (khác
điểm ) sao cho . Đường thẳng cắt đường thẳng tại điểm , đường thẳng cắt đường thẳng tại
điểm .
a) Chứng minh rằng: Tứ giác nội tiếp và .
b) Chứng minh rằng đường thẳng vuông góc với đường thẳng .
c) Đường thẳng cắt đường tròn tại điểm (khác điểm ), đường thẳng cắt đường tròn tại
điểm (khác điểm ), đường thẳng cắt đường thẳng tại điểm . Chứng minh rằng ba điểm thẳng
hàng.
Câu 5 (1,5 điểm).
1)Trong một giải bóng đá có 12 đội tham dự, thi đấu vòng tròn 1 lượt (2 đội bất kỳ đấu với
nhau đúng 1 trận).
a) Chứng minh rằng sau 4 vòng đấu luôn tìm được ba đội đôi một chưa thi đấu với
nhau.
b) Khẳng định trên còn đúng không nếu mỗi đội đã đấu đúng 5 trận?
2) Gieo hai con xúc sắc đồng chất, có màu khác nhau. Tính xác suất để được tổng số chấm
trên hai mặt con xúc xắc bằng 7.
…………………Hết………………..

PHÒNG GIÁO DỤC VÀ
ĐÀO TẠO TAM ĐIỆP
Trường THCS Đồng Giao
HƯỚNG DẪN CHẤM ĐỀ THI TUYỂN SINH 10 CHUYÊN
Năm 2024
MÔN: TOÁN
(Hướng dẫn chấm gồm 05 trang)
Chú ý:
-Thí sinh làm theo cách khác nếu đúng thì cho điểm tương đương.
- Điểm bài thi không làm tròn.
Câu
1
(2 điểm)
Đáp án Điểm
1) (1 điểm). Cho đa thức với có. Tính giá trị của
Đặt
Đặt
Với ta có
mà là số vô tỉ nên
Thay ta có
0,25
0,25
0,25
0,25
2) (1 điểm). Giải hệ phương trình .
ĐK: .
Với thay vào ta được
.
Với thay vào ta được
.
Vậy hệ phương trình có bốn nghiệm là:
;;;.
0,25
0,25

0,25
0,25
2
(2 điểm)
1) (1 điểm). Biết và số dư trong phép chia đa thức cho bằng 17.
Chứng minh rằng giá trị của đa thức Q tại là một số nguyên tố.
Giả sử
Thế thì:
Vậy giá trị của đa thức Q tại là một số nguyên tố.
0,25
0,25
0,25
0,25
2) (1 điểm). Cho . Tìm giá trị nhỏ nhất của biểu thức:
Ta có BĐT:
Thật vậy BĐT trên tương đương với:
Dấu bằng xảy ra khi
Áp dụng BĐT vừa chứng minh và BĐT: AM-GM ta có:
Dấu bằng xảy ra khi
Vậy GTNN của P là Khi
0,25
0,25
0,25
0,25














![Dàn ý và bài văn mẫu nghị luận xã hội ôn thi vào lớp 10: Tài liệu [mô tả/định tính]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250824/levanphuong15081979@gmail.com/135x160/23851756089220.jpg)











