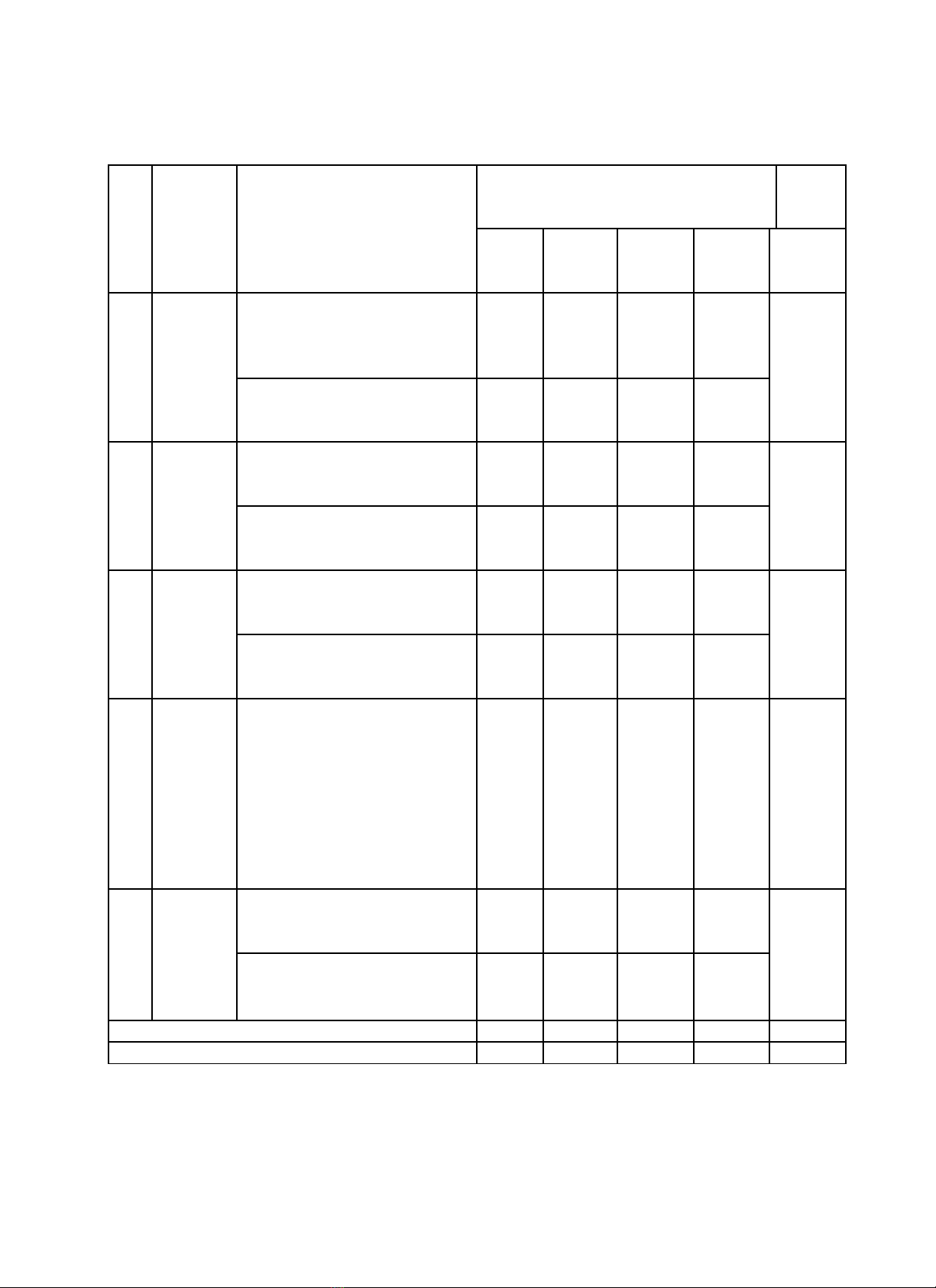
MA TRẬN ĐỀ THI TUYỂN SINH LỚP 10 THPT
Năm 2024
Bài thi môn chuyên: Toán
T
T
Chươn
g/Chủ
đề
Nội dung/đơn vị kiến thức
Số câu hỏi theo mức độ nhận thức Tổng
%
điểm
Nhận
biết
Thông
hiểu
Vận
dụng
Vận
dụng
cao
1 BIến
đổi đại
số
Rút gọn, tính giá trị biểu thức
chứa nhiều biến trong đó có
điều kiện liên hệ giữa các
biến.
1
C1a
1 đ 2 điểm
20%
Phương trình, hệ phương
trình; bất phương trình
1
C1b
1 đ
2 Đa
thức và
bất
đẳng
thức
Đa thức. 1
C2a
1 đ 2 điểm
20%
Bất đẳng thức; tìm giá trị lớn
nhất, nhỏ nhất của biểu thức.
1
C2b
1đ
3 Số học Quan hệ chia hết
Số chính phương, số lập
phương
1
C3a
0,75 đ 1,5
điểm
15%
Phần nguyên, phương trình
nghiệm nguyên.
1
C3b
0,75 đ
4Hình
học
phẳng
Các phương pháp chứng
minh tứ giác nội tiếp, hai
tam giác bằng nhau, hai tam
giác đồng dạng, ba điểm
thẳng hàng. Các phương
pháp chứng minh tứ giác nội
tiếp, hai tam giác bằng nhau,
hai tam giác đồng dạng, ba
điểm thẳng hàng.
1
C4a
1 đ
1
C4b
1 đ
1
C4c
1 đ
3 điểm
30%
5 Tổ hợp Bài toán đếm
Thống kê và xác xuất
1
C5a
0,75 đ 1,5
điểm
15%
Nguyên lí Dirichlet, nguyên
lí cực trị.
1
C5b
0,75 đ
Tổng 0 3 4,25 2,75
Tỉ lệ % 0% 30% 42,5% 27,5%
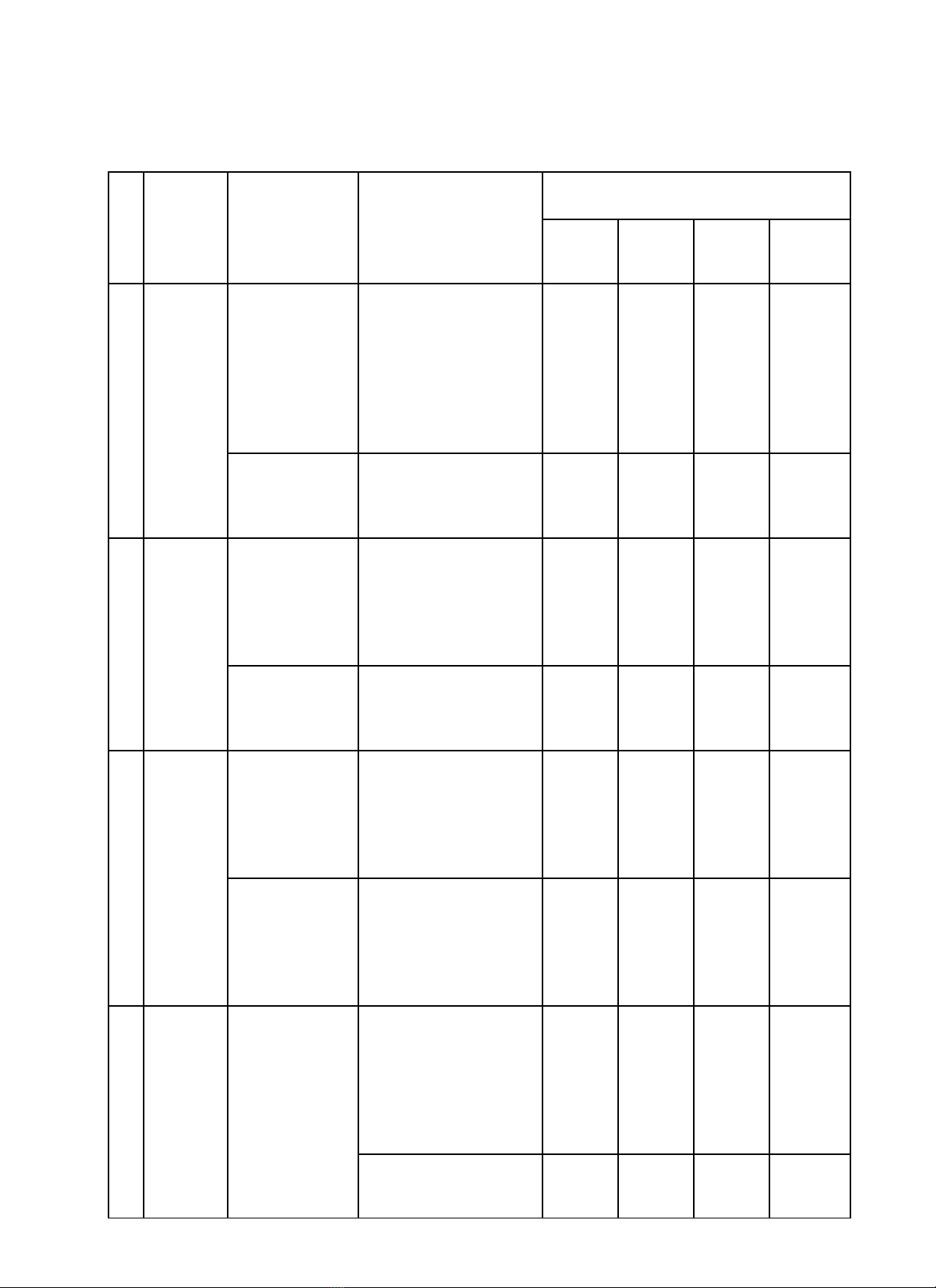
BẢN ĐẶC TẢ ĐỀ THI TUYỂN SINH LỚP 10 THPT
Năm 2024
Bài thi môn chuyên: Toán
T
T
Chươn
g/
Chủ đề
Nội dung/Đơn
vị kiến thức MưRc đôS đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận
biêt
Thông
hiểu
Vận
dụng
Vận
dụng
cao
1
Biến
đổi đại
số
Rút gọn, tính
giá trị biểu
thức chứa
nhiều biến
trong đó có
điều kiện liên
hệ giữa các
biến.
Thông hiểu
Tính được giá trị của
biểu thức chứa biến
khi biết giá trị của
biến
1TL
Câu 1a
Phương trình,
hệ phương
trình; bất
phương trình
Thông hiểu
Giải được hệ phương
trình hai ẩn
1TL
Câu
1b
2
Đa
thức và
bất
đẳng
thức
Đa thức Vận dụng
- Vận dụng định nghĩa
phép chia đa thức để
chứng minh đa thức
không có nghiệm
nguyên
1TL
Câu 2a
Bất đẳng thức
Cauchy
VâXn duXng:
Biết vận dụng bất đẳng
thức Cauchy để chứng
minh bất đẳng thức
1TL
Câu 2b
3
Số học
Số chính
phương
Vận dụng :
- Vận dụng khái niệm
số hữu tỉ, quan hệ
chia hết tìm giá trị của
biến để một biểu thức
là số chính phương
1TL
Câu 3a
Phương trình
nghiệm
nguyên
Vận dụng :
Sử dụng công thức
nghiêm của phương
tình bậc hai để tìm
nghiệm nguyên của
phương trình
1TL
Câu 3b
4
Hình
học
phẳng
Hai tam giác
đồng dạng, tứ
giác nội tiếp,
hệ thức lượng
trong đường
tròn
Thông hiểu:
- Sử dụng tính chất của
tứ giác nội tiếp để
chứng minh các góc
bằng nhau từ đó chứng
minh được các tam
giác đồng dạng
1TL
Câu 4a
Vận dụng:
- Vận dụng định nghĩa
hai tam giác đồng dạng
1TL
Câu 4b
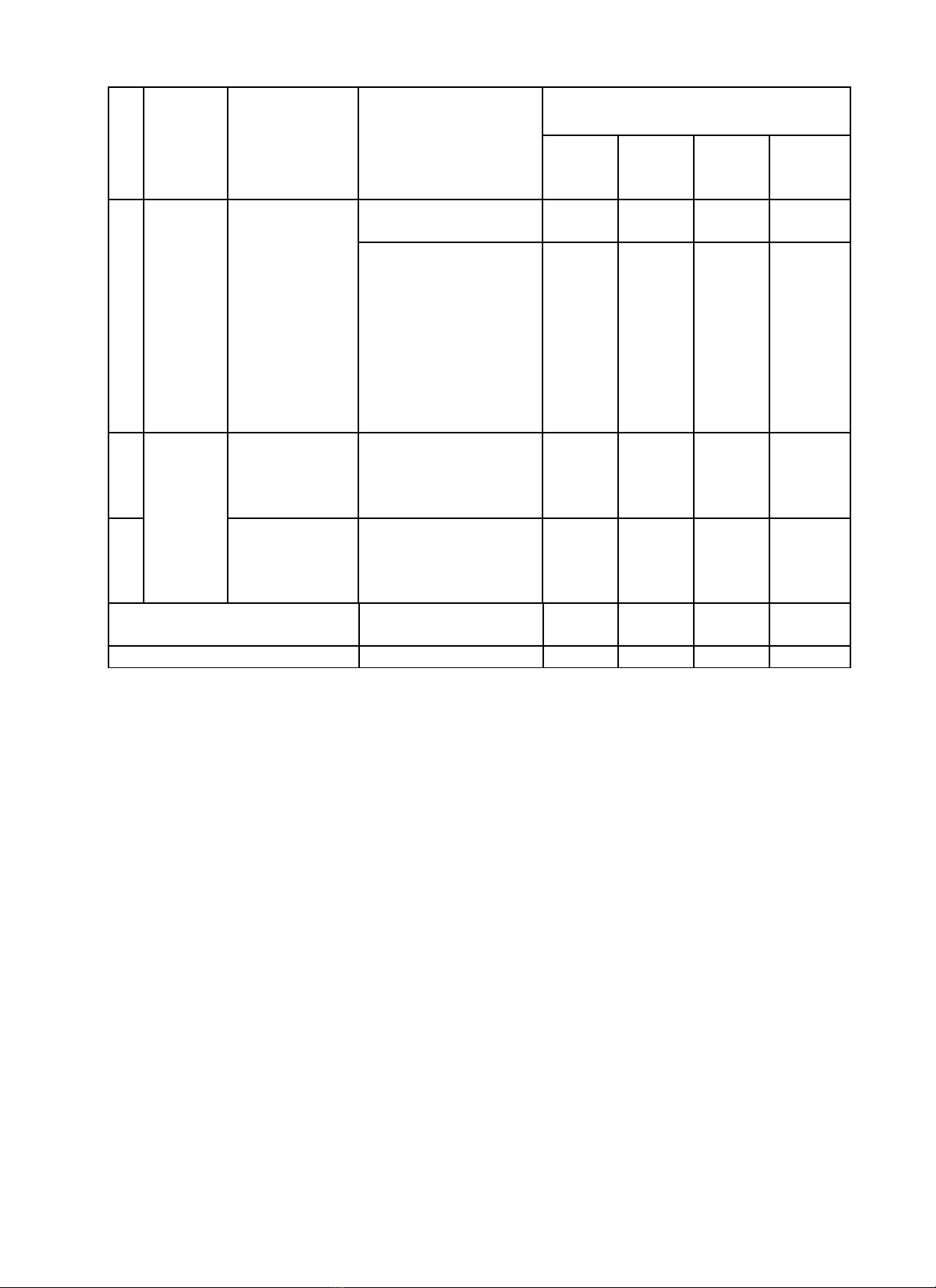
T
T
Chươn
g/
Chủ đề
Nội dung/Đơn
vị kiến thức MưRc đôS đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận
biêt
Thông
hiểu
Vận
dụng
Vận
dụng
cao
để tính độ dài đoạn
thẳng
Vận dụng cao:
- Vận dụng định nghĩa
hai tam giác đồng dạng
và hệ thức lượng trong
đường tròn để chứng
minh một điểm luôn
thuộc một đường thẳng
cố định.
1TL
Câu 4c
5
Tổ hợp
Bài toán đếm Vận dụng:
- Sử dụng quy tắc đếm
để giải quyết bài toán
thực tế.
1TL
Câu 5a
Nguyên lí
Đirichlet
Vận dụng:
- Vận dụng nguyên lí
Đirichlet để giải quyết
bài toán thực tế.
1TL
Câu 5b
Tổng 0 điểm 3 điểm 4,25
điểm
2,75
điểm
Tỉ lệ % 30% 42,5% 27,5%
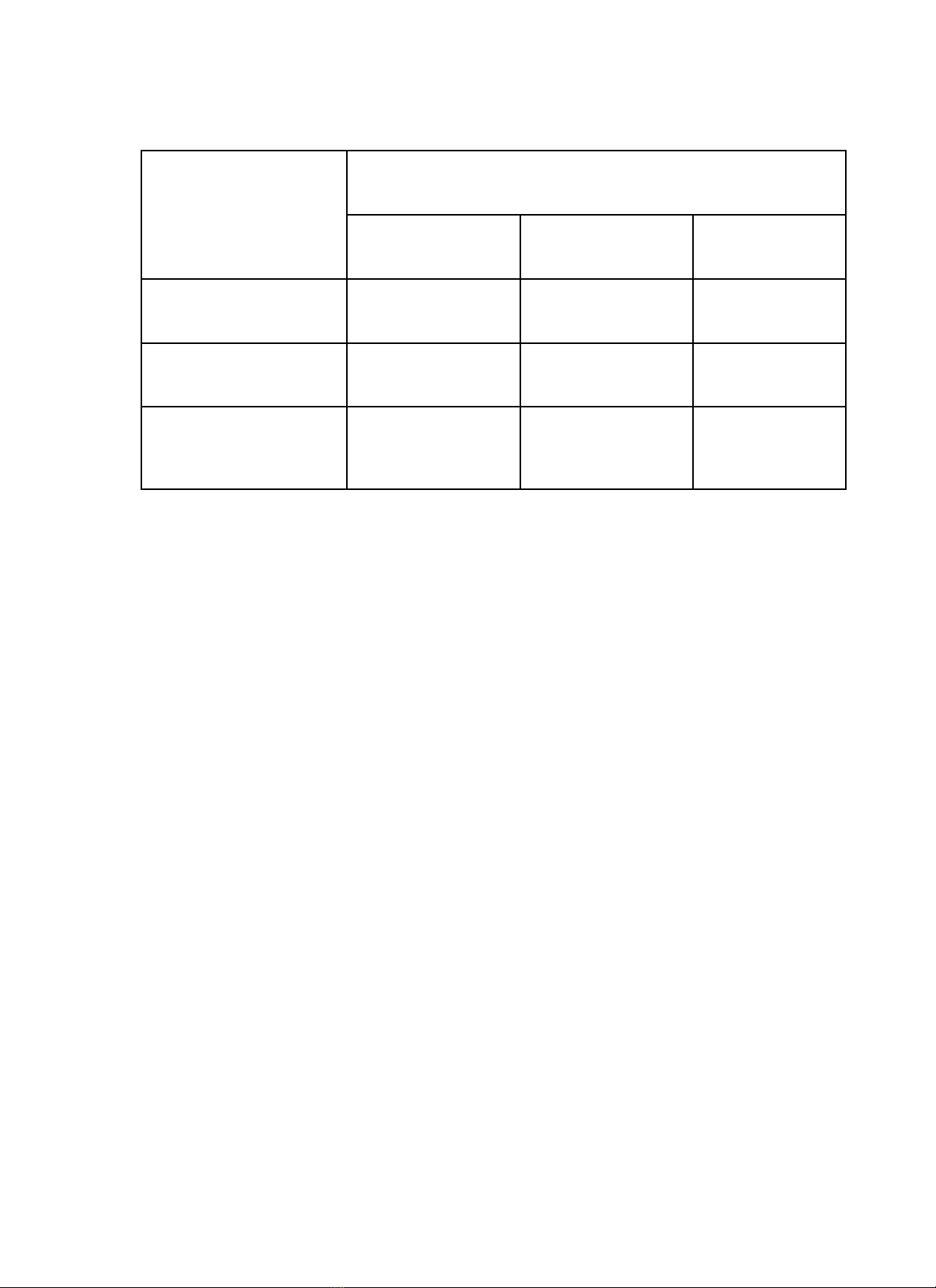
BẢNG NĂNG LỰC VÀ CẤP ĐỘ TƯ DUY ĐỀ THI TUYỂN SINH 10 THPT CHUYÊN
Môn: TOÁN
Năng lực
Cấp độ tư duy
Thông hiểu Vận dụng Vận dụng cao
Tư duy và lập luận
Toán học
1
(Câu 1ab)
1
(Câu 2a ; 3b; 4b) 0
Giải quyết vấn đề Toán
học
1
(Câu 4a)
3
(Câu 5ab)
4
(Câu 2b, 3a, 4c)
Tổng
(Số lệnh hỏi của từng
cấp độ tư duy)
3 5 3
PHÒNG GD&ĐT HOA LƯ
TRƯỜNG THCS NINH THẮNG
ĐỀ THI TUYỂN SINH LỚP 10 THPT
Năm 2024
MÔN THI CHUYÊN: TOÁN
Thời gian làm bài: 150 phút
(Đề thi gồm 05 câu, 01 trang)
Câu 1: (2,0 điểm)
a) Cho
, ,abc
là các số thực khác 0, thỏa mãn
2 2
a ab c bc
+ = +
và
2 2
c ac b ab
+ = +
. Tính giá trị
của biểu thức
1 1 1
a b c
Mb c a
= + + +
b) Giải hệ phương trình
2 2
2
4 1 0
( 1)( 2)
x y xy y
x x y y
+ + − + =
+ + − =
Câu 2: (2,0 điểm)
a) Cho đa thức
( )
P x
với các hệ số nguyên thỏa mãn
( ) ( )
P 1 .P 2 3.=
Chứng minh rằng đa thức
( )
P x 4-
không có nghiệm nguyên.
b) Cho ba số thực
a
,
,
>
thoả mãn a + b + c = 2025.
Chứng minh
a b c
+ + 1
a + 2025a + bc b + 2025b + ca c + 2025c + ab
.
Câu 3: (1,5 điểm)
a) Tìm tất cả các số hữu tỉ x sao cho giá trị của biểu thức x2 - x + 5 là một số chính phương.
b) Tìm các nghiệm nguyên (x; y) của phương trình:
2 2
5(x xy y ) 7(x 2y)
+ + = +
.
Câu 4: ( 3 điểm).
Cho đường tròn
( )
O;R
và điểm
A
cố định với
OA 2R
=
, đường kính BC chuyển động sao cho
tam giác
ABC
là tam giác nhọn. Đường tròn ngoại tiếp tam giác ABC cắt đường thẳng
OA
tại điểm
thứ hai là
I
. Các đường thẳng
AB,AC
cắt đường tròn
(O)
lần lượt tại điểm thứ hai là
D
và
E
. Gọi
K
là giao điểm của
DE
và
AO
.
a) Chứng minh rằng:
AEK
∆
và
AIC
∆
đồng dạng.
b) Tính độ dài của đoạn
AK
theo
R
.
c) Chứng minh rằng tâm đường tròn ngoại tiếp
ADE
∆
luôn thuộc một đường thẳng cố định.
Câu 5: (1,5 điểm)
a. Có 12 chiếc ghế xếp vòng quanh 1 bàn tròn được đánh số thứ tự từ 1 đến 12. Có 6 học sinh nam
và 6 học sinh nữ được xếp ngồi vào bàn đó. Hỏi có bao nhiêu cách sắp xếp vị trí sao cho nam và nữ
ngồi xen kẽ nhau.
b. Kì thi tuyển sinh vào lớp 10 phổ thông trung học năm học 2024 – 2025 trường THPT chuyên
Lương Văn Tụy tỉnh Ninh bình có 459 đến từ 8 địa phương khác nhau đỗ vào trường. Biết rằng nhà
trường tuyển sinh 13 lớp chuyên. Chứng minh rằng có ít nhất một lớp chuyên có 5 học sinh ở cùng
một địa phương.
…………..Hết…………..