PHÒNG GIÁO DỤC YÊN MÔ
TRƯỜNG THCS YÊN THẮNG
ĐỀ THI TUYỂN SINH LỚP 10 THPT
Năm 2024
Bài thi môn chuyên: Toán
1_Toan_PG7_TS10C_2024_DE_SO_12 Thời gian làm bài:150 phút (không kể thời gian phát đề)
MA TRẬN ĐỀ THI TUYỂN SINH LỚP 10 THPT
TT
Nội
dung
kiến
thức
Mức
độ
nhận
thức
Tổng Tỉ lệ % tổng điểm
Thông
hiểu
Vận
dụng
Vận
dụng
cao
Số CH Số
điểm
Thời
gian Số CH Số
điểm
Thời
gian
Số
CH
Số
điểm
Thời
gian
Số
CH
Số
điểm
Thời
gian
1
Rút gọn,
tính giá trị
biểu thức
nhiều
biến
trong đó
có điều
kiện liên
hệ giữa
các biến.
1 1 10 1 1 10 10
2Phương
trình vô tỉ. 1 1 10 1 1 10 10
3
hệ số của
đa thức,
bậc của
đa thức.
1 1 15 1 1 15 10
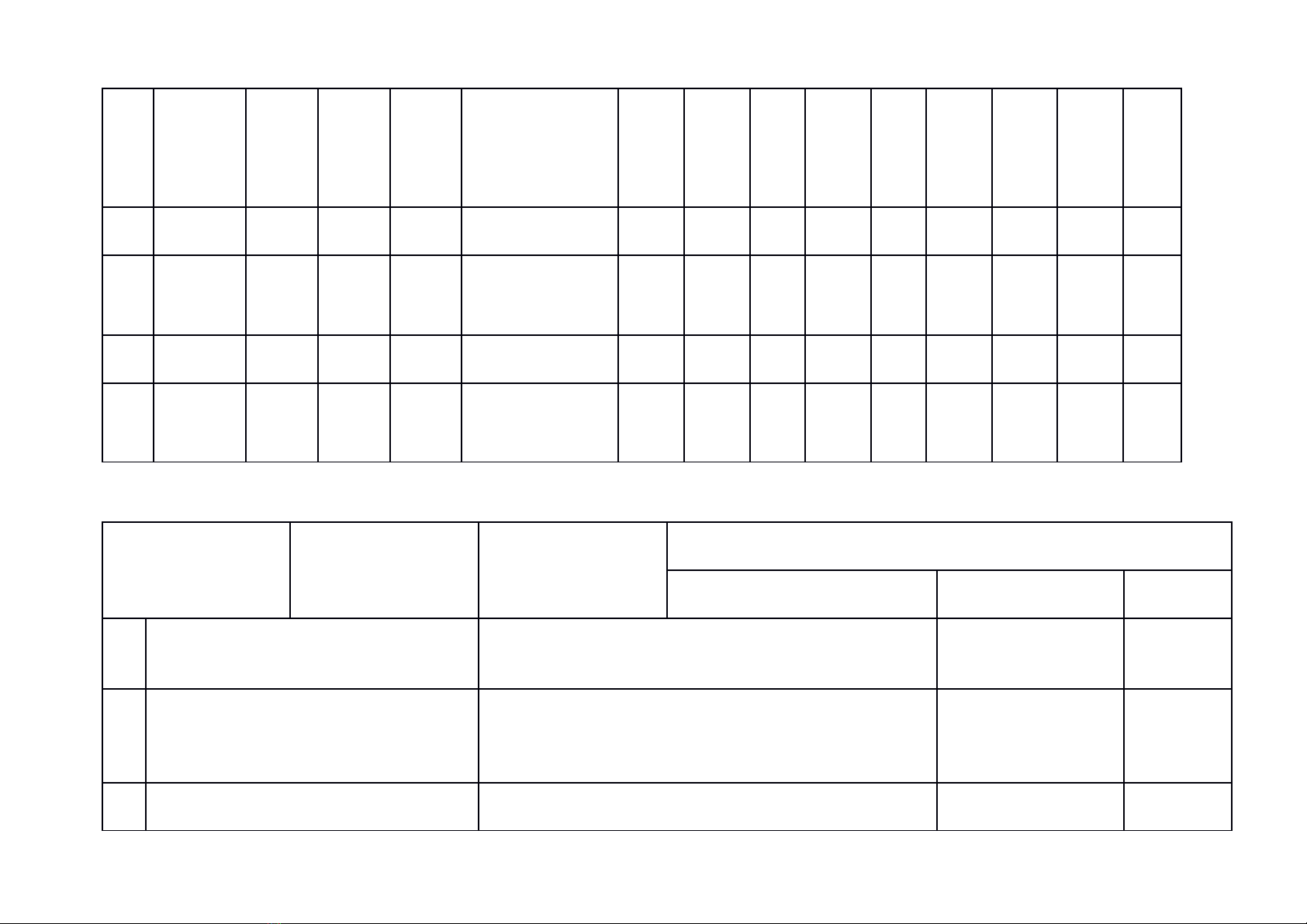
4
Bất đẳng
thức; tìm
giá trị nhỏ
nhất của
biểu
thức.
1 1 20 1 1 20 10
5Quan hệ
chia hết 1 1 20 1 1 20 10
6
phương
trình
nghiệm
nguyên.
1 1 10 1 1 10 10
7Hình học
phẳng 1 1 10 1 1 15 1 1 20 3 3 45 30
8
Nguyên lí
Dirichlet,
nguyên lí
cực trị
1 1 20 1 1 20 10
ĐẶC TẢ ĐỀ THI. (Bài thi môn chuyên: Toán)
TT Nội dung kiến thức
Mức độ kiến thức,
kĩ năng cần đánh
giá
Số câu hỏi theo mức độ
Vận
dụng
Vận dụng
cao
1
Rút gọn, tính giá trị biểu thức nhiều
biến trong đó có điều kiện liên hệ giữa
các biến.
- Vận dụng các phép biến đổi để rút gọn
- Vận dụng hẳng thức tổng hai lập phương linh hoạt.
- Vận dụng kĩ năng phân tích thành nhân tử.
1
2 Phương trình vô tỉ.
- Thông hiểu các bước giải phương trình vô tỉ
- Biết tìm điều kiện để phương trình có nghĩa và đối
chiếu điều kiện khi có kết quả.
- Hiểu cách đặt ẩn phụ để giải bài toán dễ hơn.
3 hệ số của đa thức, bậc của đa thức. - Vận dụng nghiệm của đa thức, định lí Bezout, …
- Giá trị đa thức, hệ số của đa thức, bậc của đa thức 1
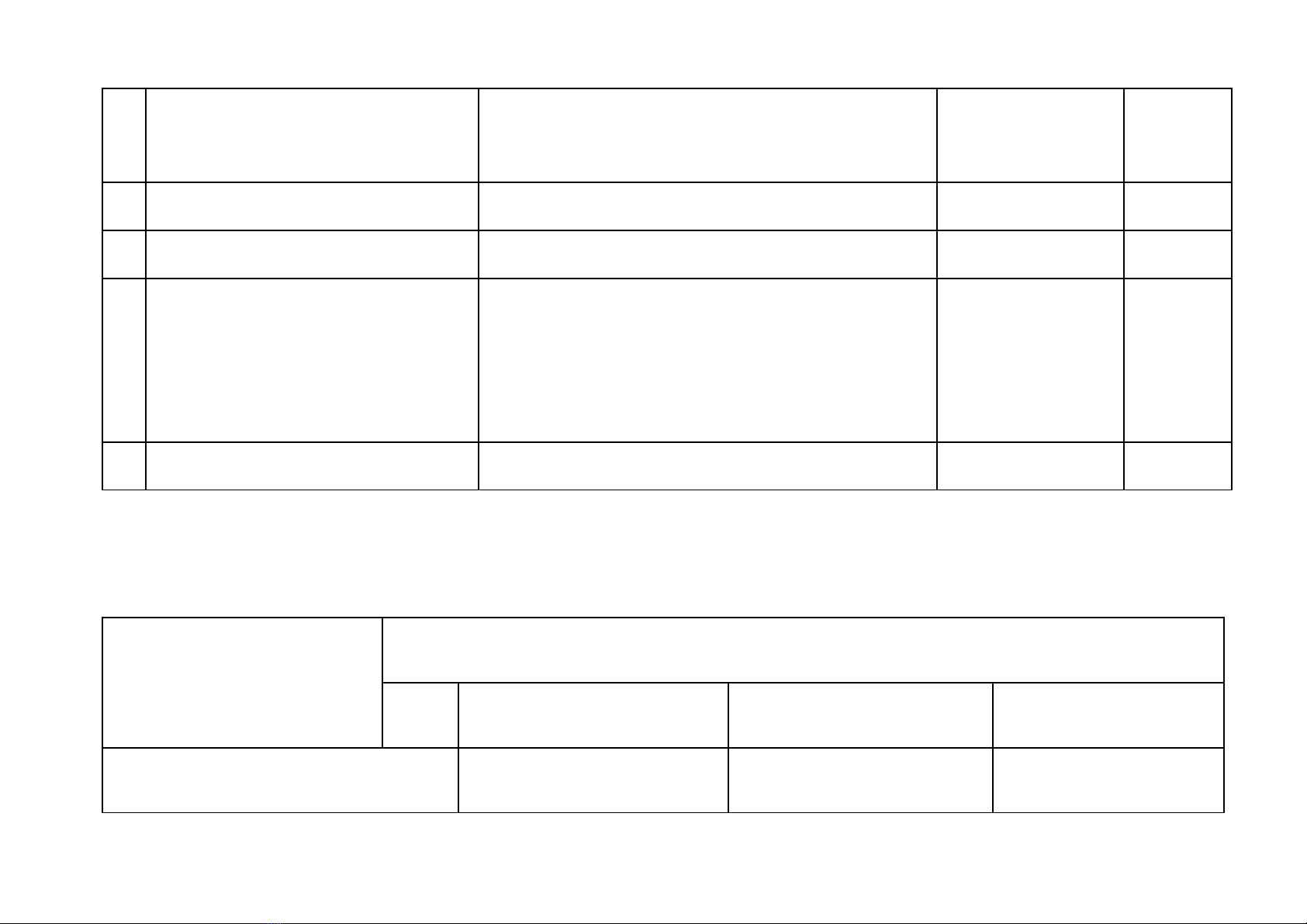
4Bất đẳng thức; tìm giá trị nhỏ nhất của
biểu thức.
- Vận dụng tính chất bất đẳng thức: tìm giá trị nhỏ
nhất của biểu thức.
- Ứng dụng của bất đẳng thức AM-GM, Cauchy-
Schwarz, …
1
5 Quan hệ chia hết - Vận dụng tính chất quan hệ chia hết, số nguyên tố
- Vận dụng hằng đẳng thức mở rộng. 1
6 phương trình nghiệm nguyên. - Vận dụng dấu hiệu chia hết, Tính chia hết của số
chính phương 1
7 Hình học phẳng
- Thông hiểu: cách vẽ hình, cách chứng minh tứ giác
nội tiếp, cách chứng minh 3 điểm thẳng hàng dẫn đến
vuông góc
- Vận dụng: Tính chất tứ giác nội tiếp, tính chất góc
kề bù.
- Vận dụng cao: Hai tam giác đồng dạng để có hệ
thức. Sử dụng kiến thức bất đẳng thức để có đpcm
1 1
8 Nguyên lí Dirichlet, nguyên lí cực trị Bài toán đếm; Nguyên lí Dirichlet 1
BẢNG NĂNG LỰC VÀ CẤP ĐỘ TƯ DUY ĐỀ THI TUYỂN SINH 10 THPT CHUYÊN
Môn: TOÁN
Năng lực
Cấp độ tư duy
Thông hiểu Vận dụng Vận dụng cao
Tư duy và lập luận Toán học 1
(Câu 1b)
2
(Câu 1a; 2a) 0
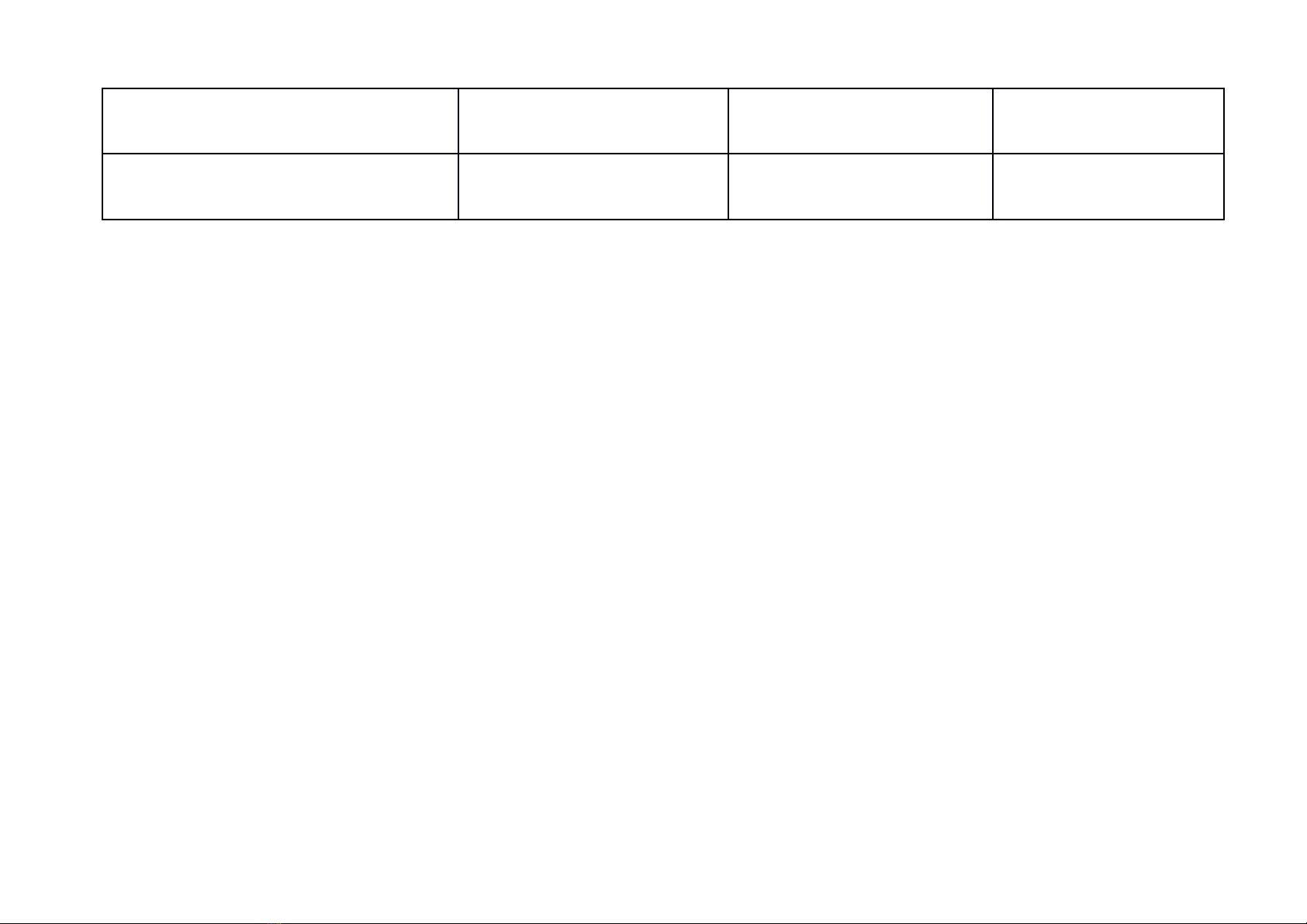
Giải quyết vấn đề Toán học 1
(Câu 4a)
2
(Câu 3b, 4b)
4
(Câu 2b, 3a, 4c, 5)
Tổng
(Số lệnh hỏi của từng cấp độ tư duy) 2 4 4
PHÒNG GIÁO DỤC YÊN MÔ
TRƯỜNG THCS YÊN THẮNG
ĐỀ THI TUYỂN SINH LỚP 10 THPT
Năm 2024
Bài thi môn chuyên: Toán
Thời gian làm bài:150 phút (không kể thời gian phát đề)
Đề thi gồm 05 bài trong 01 trang
Bài 1 (2,0 điểm).
a) Cho các số thực thỏa mãn .
Tính giá trị biểu thức:
b) Giải phương trình:
Bài 2 (2,0 điểm).
a) Cho đa thứclà đa thức bậc 4 thỏa mãn và .
Xác định .
b) Cho các số thực dương và . Tìm giá trị nhỏ nhất của biểu thức:
Bài 3 (2,0 điểm).
a) Cho là số nguyên thỏa mãn . Chứng minh
b) Tìm các số nguyên thỏa mãn .
Bài 4 (3,0 điểm).
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Đường cao BD và CE của tam giác ABC cắt nhau tại H. Vẽ đường kính AI của đường
tròn (O), đường thẳng HI cắt BC tại M. Đường tròn ngoại tiếp tam giác AED cắt đường tròn (O) tại N và cắt đường thẳng AM tại K (N và
K khác A). Gọi F là giao điểm của AN và BC. Chứng minh rằng:
a) HI vuông góc với AN.
b) Ba điểm D; E; F thẳng hàng.