LỚP TOÁN THẦY CHÍ ĐỀ SỞ HÀ NỘI (VÒNG 1), 2022-2023
HƯỚNG DẪN GIẢI ĐỀ THI TUYỂN SINH SỞ HÀ NỘI VÒNG 1
Bài 1. (2,0 điểm) Cho hai biểu thức A=x+ 2
√xvà B=2√x−3
√x−1+3−√x
x−1với x >
0, x = 1.
1. Tính giá trị biểu thức Akhi x= 9.
2. Chứng minh B=2√x
√x+ 1.
3. Tìm tất cả giá trị của xđể A.B = 4.
Lời giải:
1. Thay x= 9 (tmđk) vào A, ta có A=x+ 2
√x=9 + 2
√9=11
3.
2. Ta có B=2√x−3
√x−1+3−√x
x−1=(2√x−3)(√x+ 1) + 3 −√x
(√x−1)(√x+ 1) =2x−2√x
(√x−1)(√x+ 1)
=2√x(√x−1)
(√x−1)(√x+ 1) =2√x
√x+ 1 .□
3. Ta có 4 = A.B =x+ 2
√x·2√x
√x+ 1 ⇔x+ 2 = 2(√x+ 1) ⇔x= 2√x⇔x= 4 (do
x > 0, x = 1)
Vậy x= 4.
Bài 2. (2,0 điểm)
1. Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Theo kế hoạch, một phân xưởng phải làm xong 900 sản phẩm trong một số ngày
quy định. Thực tế, mỗi ngày phân xưởng đã làm được nhiều hơn 15 sản phẩm so
với số sản phẩm phải làm một ngày theo kế hoạch. Vì thế 3 ngày trước khi hết thời
hạn, phân xưởng đã làm xong 900 sản phẩm. Hỏi, theo kế hoạch, mỗi ngày phân
xưởng phải làm bao nhiêu sản phẩm? (Giả định rẳng số sản phẩm mà phân xưởng
làm được trong mỗi ngày là bằng nhau.)
2. Một khối gỗ dạng hình trụ có bán kính đáy là 30cm và chiều cao là 120cm. Tính
thể tích khối gỗ đó (lấy π≈3,14).
Lời giải:
1. Gọi số sản phẩm mỗi ngày phân xưởng phải làm theo kế hoạch là x(sản phẩm) (x∈N∗)
⇒số ngày làm theo kế hoạch là 900
x(ngày)
Theo đề bài, ta có phương trình (x+ 15) 900
x−3= 900 ⇔3x2+ 45x−13500 = 0
⇔(x−60)(x+ 75) = 0 ⇔x= 60 (tmđk)
Vậy phân xưởng dự kiến mỗi ngày làm được 60 sản phẩm.
038.3070.253
LỚP TOÁN THẦY CHÍ ĐỀ SỞ HÀ NỘI (VÒNG 1), 2022-2023
2. Thể tích khối gỗ là V=π.r2.h ≈3,14.302.120 = 339120cm3.
Bài 3 (2,5 điểm)
1. Giải hệ phương trình
2
x−3−3y= 1
3
x−3+ 2y= 8
2. Trong mặt phẳng tọa độ Oxy, cho parabol (P) : y=x2và đường thẳng (d) : y=
(m+ 2)x−m.
(a) Chứng minh (d)luôn cắt (P)tại hai điểm phân biệt.
(b) Gọi x1, x2là hoành độ các giao điểm của (d)và (P). Tìm tất cả các giá trị
của mđể 1
x1
+1
x2
=1
x1+x2−2.
Lời giải:
1. Điều kiện xác định: x= 3
Ta có
2
x−3−3y= 1
3
x−3+ 2y= 8 ⇒ −32
x−3−3y+ 2 3
x−3+ 2y= 8=−3 + 16
⇔13y= 13 ⇔y= 1
⇒2
x−3= 1 + 3y= 4 ⇔x=7
2(tmđk)
Vậy x=7
2và y= 1.
2. Xét pthđgđ x2= (m+ 2)x−m⇔x2−(m+ 2)x+m= 0 (1)
(a) Ta có ∆ = (m+ 2)2−4m=m2+ 4 >0∀m⇔Phương trình (1) có hai nghiệm
phân biệt ∀m⇔(d)luôn cắt (P)tại hai điểm phân biệt .□
(b) Theo hệ thức Vi-ét, ta có x1+x2=m+ 2
x1x2=m
Điều kiện xác định x1x2= 0
x1+x2−2= 0 ⇔m= 0 Theo đề bài, ta có 1
x1
+1
x2
=
1
x1+x2−2⇔x1+x2
x1x2
=1
x1+x2−2
⇔m+ 2
m=1
m⇔m=−1(tmđk)
Vậy m=−1.
038.3070.253
LỚP TOÁN THẦY CHÍ ĐỀ SỞ HÀ NỘI (VÒNG 1), 2022-2023
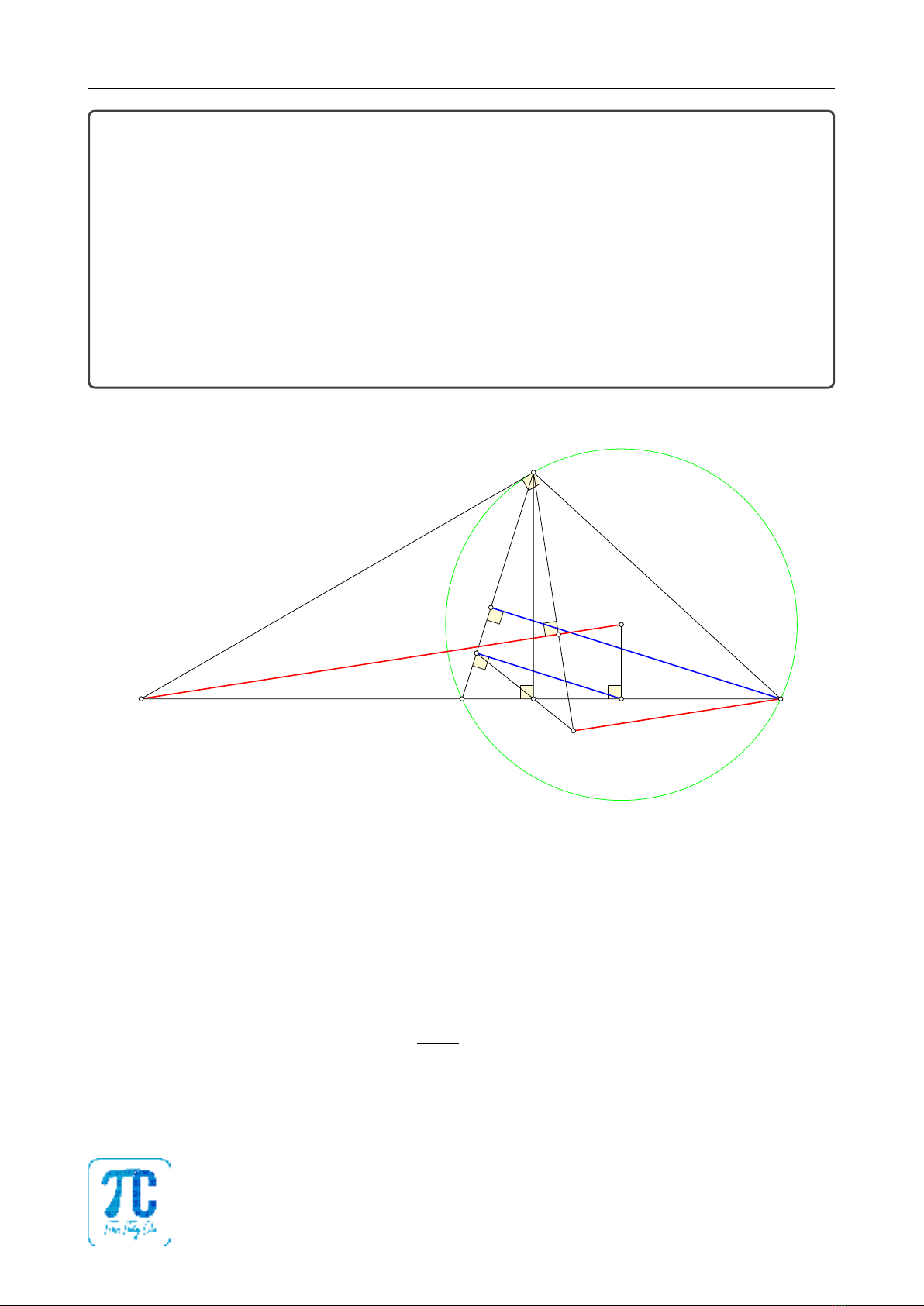
Bài 4 (3,0 điểm) Cho tam giác ABC có ba góc nhọn (AB < AC), nội tiếp đường tròn
(O). Tiếp tuyến tại điểm Acủa đường tròn (O)cắt đường thẳng BC tại điểm S. Gọi I
là chân đường vuông góc kẻ từ điểm Ođến đường thẳng BC.
1. Chứng minh tứ giác SAOI nội tiếp.
2. Gọi H, D lần lượt là chân các đường vuông góc kẻ từ điểm Ađến các đường thẳng
SO, BC. Chứng minh \
OAH =[
IAD.
3. Vẽ đường cao CE của tam giác ABC. Gọi Qlà trung điểm của đoạn thẳng BE.
Đường thẳng QD cắt đường thẳng AH tại điểm K. Chứng minh BQ.BA =BD.BI
và đường thẳng CK song song với đường thẳng SO.
Lời giải:
A
BC
S
H
ID
E
Q
K
O
1. Ta có [
SAO +d
SIO = 90◦+ 90◦= 180◦⇒Tgnt SAOI .□
2. △IAD vuông tại D⇒[
IAD = 90◦−d
AIS
△OAH vuông tại D⇒\
OAH = 90◦−[
AOS
Lại có tgnt SAOI ⇒d
AIS =[
AOS ⇒[
IAD =\
OAH .□
3. Ta có Q, I lần lượt là trung điểm BE, BC ⇒QI ∥CE ⇒[
AQI = 90◦=[
ADI ⇒Tgnt
AQDI ⇒BQ.BA =BD.BI .□
Ta có \
BAD = 90◦−[
ABC = 90◦−
[
AOC
2=[
OAC
mà [
IAD =\
OAH ⇒[
BAI =\
KAC
Lại có tgnt AQDI ⇒\
DKC =\
BDQ =[
BAI =\
KAC ⇒Tgnt ADKC
⇒\
ADC =\
AKC = 90◦
mà AH ⊥SO ⇒CK ∥SO .□
038.3070.253
LỚP TOÁN THẦY CHÍ ĐỀ SỞ HÀ NỘI (VÒNG 1), 2022-2023
Bài 5 (0,5 điểm) Cho hai số thực dương a, b thỏa mãn a+b≤2. Chứng minh
a2
a2+b+b2
b2+a≤1.
Lời giải: Ta có a2
a2+b+b2
b2+a= 2 −a
b2+a−b
a2+b
Áp dụng bđt Cauchy cộng mẫu, ta có
a
b2+a+b
a2+b=a2
a2+ab2+b2
b2+a2b≥(a+b)2
a2+b2+ab(a+b)≥(a+b)2
a2+b2+ 2ab = 1
⇒a2
a2+b+b2
b2+a≤1.□
Dấu "=" xảy ra ⇔a=b= 1
038.3070.253