SỞ GIÁO DỤC VÀ ĐÀO TẠO TÂY NINH
KÌ THI TUYỂN SINH VÀO LỚP 10 NĂM HỌC 2019 – 2020
Ngày thi : 01 tháng 6 năm 2019
Môn thi : TOÁN (không chuyên)
Thời gian làm bài : 120 phút (không kể thời gian giao đề)
-------------------------------------------------------------------------------------
ĐỀ CHÍNH THỨC
(Đề thi có 01 trang, thí sinh không phải chép đề vào giấy thi)
Câu 1: (1,0 điểm)
Tính giá trị biểu thức
T 4 25 9
.
Câu 2: (1,0 điểm)
Tìm m để đồ thị hàm số
2
21y m x
đi qua điểm
A 1;
.
Câu 3: (1,0 điểm)
Giải phương trình
260xx
.
Câu 4: (1,0 điểm)
đồ thị của hàm số
2
yx
.
Câu 5: (1,0 điểm)
Tìm tọa độ giao điểm của đường thẳng
1
d : 2 1yx
và đường thẳng
Câu 6: (1,0 điểm)
Cho tam giác ABC vuông cân tại A có đường trung tuyến BM (M thuộc cạnh AC).. Biết
AB 2a
. Tính theo a độ dài AC, AM và BM.
Câu 7: (1,0 điểm)
Hai ô tô khởi hành cùng một lúc đi từ A đến B. ận tốc của ô tô thứ nhất lớn hơn vận tốc
của ô tô thứ hai là 10km/h nên ô tô thứ nhất đến B trước ô tô thứ hai
1
2
giờ. Tính vận tốc của
mỗi ô tô. Biết rằng quãng đường AB dài 150km.
Câu 8: (1,0 điểm)
Tìm các giá trị nguyên của m để phương trình
24 m +1 0 xx
có hai nghiệm phân biệt
1
x
và
2
x
thỏa
33
12
100xx
.
Câu 9: (1,0 điểm)
Cho tam giác ABC có ba góc nhọn và nội tiếp đường tròn tâm O. Gọi I là trung điểm AB,
đường thẳng qua I vuông góc AO và cắt cạnh AC tại J. Chứng minh bốn điểm B, C, J và I
cùng thuộc một đường tròn.
Câu 10: (1,0 điểm)
Cho đường tròn (C) có tâm I và có bàn kính
R2a
. Xét điểm M thay đổi sao cho
IM a
.
Hai dây AC, BD đi qua điểm M và vuông góc với nhau (A, B, C, D thuộc (C)). Tìm giá trị lớn
nhất của diện tích tứ giác ABCD.
--- Hết ---
Giám thị không giải thích gì thêm.
Họ và tên thí sinh : ................................................ Số báo danh : .......................................
Chữ k của giám thị 1: ......................................... Chữ k của giám thị 2 : ........................
BÀI GIẢI
Câu 1: (1,0 điểm)
T 4 25 9 2 5 3 4
.
Câu 2: (1,0 điểm)
Đồ thị hàm số
2
21y m x
đi qua điểm
A 1;
.
2
2 1 .1 5m
2 1 5m
2m
Câu 3: (1,0 điểm)
260xx
2
1 4.1. 6 25 0
,
5
.
1
15 3
2
x
;
2
15 2
2
x
.
ậy
S = 2; 3
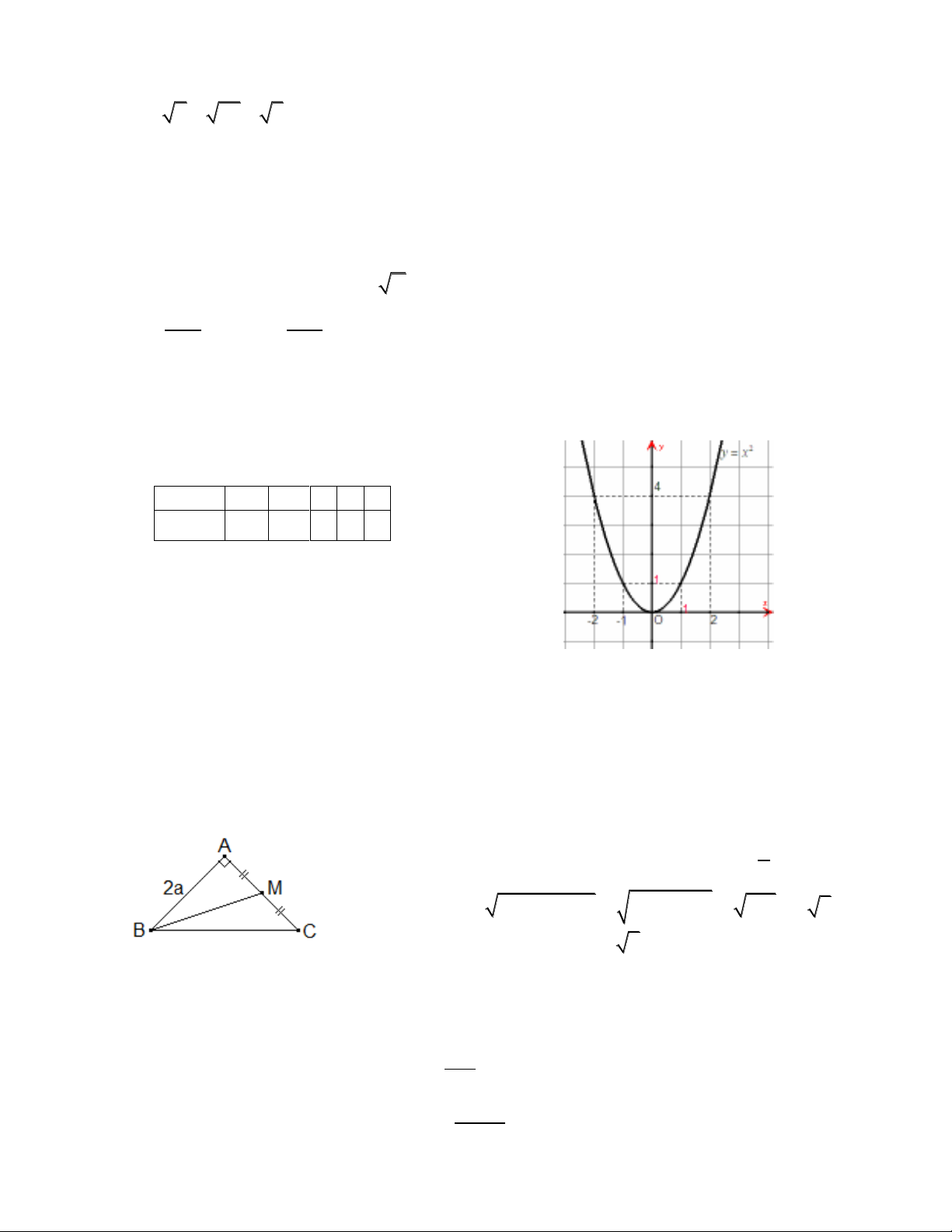
Câu 4: (1,0 điểm)
đồ thị của hàm số
2
yx
BGT
x
2
1
0
1
2
2
yx
4
1
0
1
4
Câu 5: (1,0 điểm)
Tọa độ giao điểm A của
d1
và
d2
là nghiệm hệ phương trình:
21
3
yx
yx


2 1 3
3
xx
yx

2
5
x
y
ậy
d1
và
d2
cắt nhau tại
A 2;
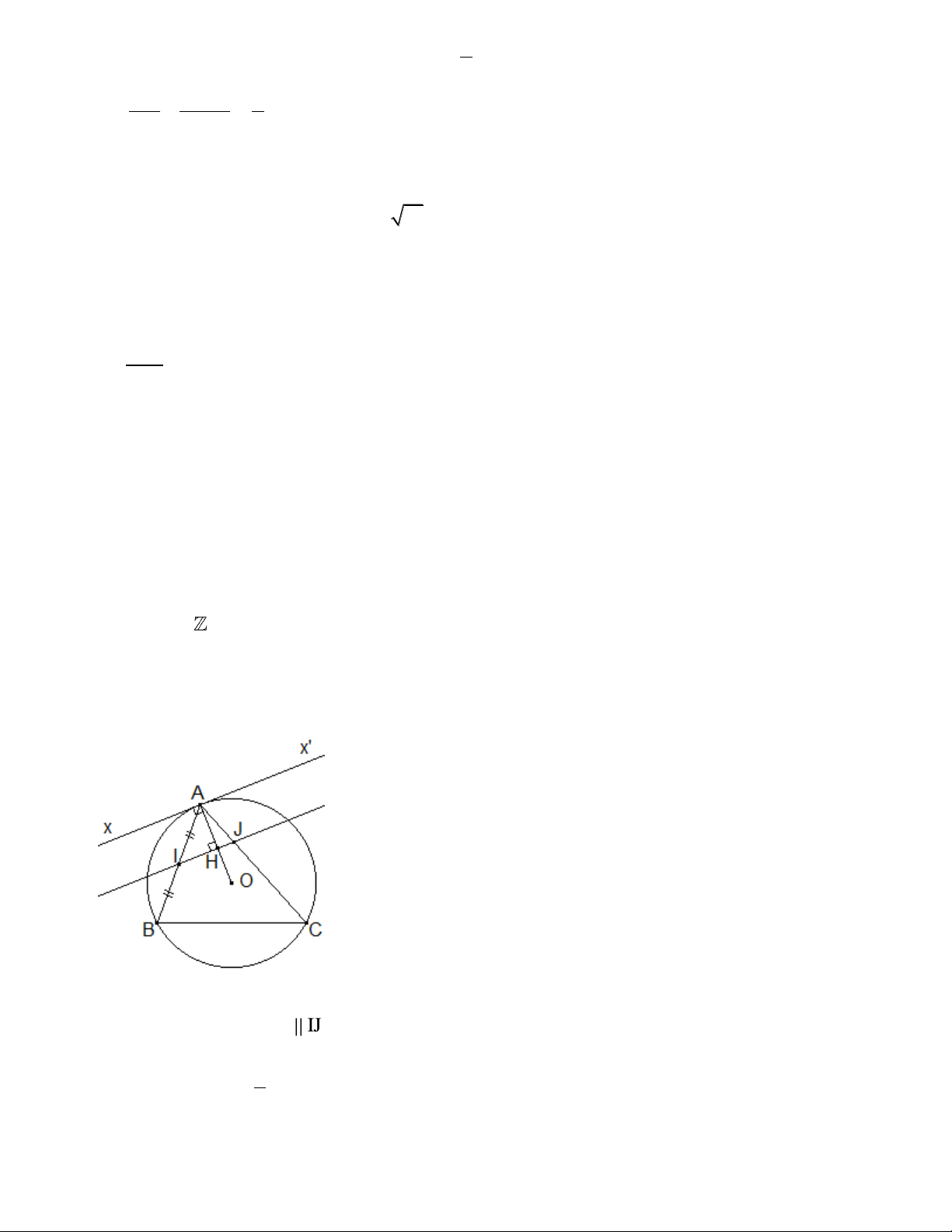
Câu 6: (1,0 điểm)
ABC
vuông cân tại A nên
AC = AB 2a
,
1
AM = AC a
2
.
ABM
có
2
2 2 2 2
BM = AB AM 2a a 5a a 5
ậy :
AC 2a
,
AM = a
,
BM a 5
Câu 7: (1,0 điểm)
Gọi vận tốc của ô tô thứ hai là
x
(km/h)
0x
.
ận tốc của ô tô thứ nhất là
10x
(km/h)
Thời gian ô tô thứ hai đi từ A đến B là
150
x
(giờ)
Thời gian ô tô thứ nhất đi từ A đến B là
150
10x
(giờ)
ì ô tô thứ nhất đến B trước ô tô thứ hai
1
2
giờ nên ta có phương trình:
150 150 1
10 2xx

0x
10 300 10 300x x x x
210 3000 0xx
2
' 5 1. 3000 3025 0
,
' 55
15 55 50 x
(nhận);
25 55 60 x
(loại)
ậy vận tốc của ô tô thứ hai là 50km/h, vận tốc của ô tô thứ nhất là
50 10 60
km/h.
Câu 8: (1,0 điểm) Tìm các giá trị nguyên của m để phương trình
24 m +1 0 xx
có hai
nghiệm phân biệt
1
x
và
2
x
thỏa
33
12
100xx
.
Giải:
24 m +1 0 xx
2
' 2 1. m 1 4 m 1 3 m
Phương trình có hai nghiệm phân biệt
'0
m30
m3
(*)
Theo Vi-ét
m
12
12
4
.1
xx
xx
33
12
100xx
3
1 2 1 2 1 2
3 100 x x x x x x
3
4 3.4. m 1 100
64 12m 12 100
12m 48
m > 4
(**)
(*) và (**)
m43
Do
m
nên
m3; 2; 1; 0;1; 2
Câu 9: (1,0 điểm)
Cho tam giác ABC có ba góc nhọn và nội tiếp đường tròn tâm O. Gọi I là trung điểm AB,
đường thẳng qua I vuông góc AO và cắt cạnh AC tại J. Chứng minh bốn điểm B, C, J và I
cùng thuộc một đường tròn.
Kẻ tiếp tuyến x’Ax với đường tròn O)
Ax OA
Ta có
Ax OA IJ
IJ OA Ax
BAx AIJ
(so le trong) (1)
Mà
BAx ACB AB
1sñ
2

(2)
(1) và (2)
AIJ ACB
Tứ giác BCJI nội tiếp được.
Hay bốn điểm B, C, J và I cùng thuộc một đường tròn.
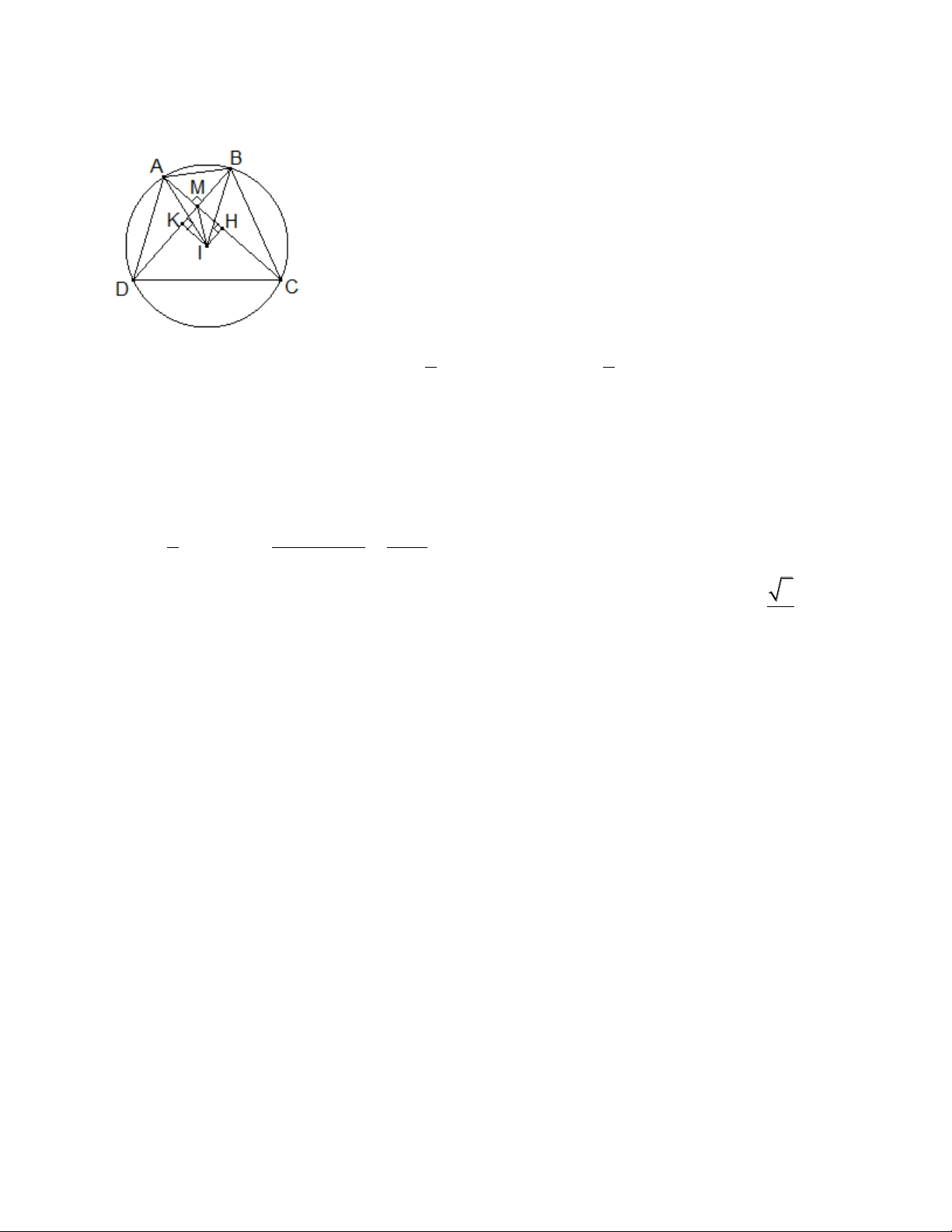
Câu 10: (1,0 điểm)
Cho đường tròn (C) có tâm I và có bàn kính
R 2a
. Xét điểm M thay đổi sao cho
IM a
.
Hai dây AC, BD đi qua điểm M và vuông góc với nhau (A, B, C, D thuộc (C)). Tìm giá trị lớn
nhất của diện tích tứ giác ABCD.
Kẻ
IH AC
,
IK BD
HA = HC = AC
1
2
và
KB = KD = BD
1
2
AIH
có
AH R IH a IH
2 2 2 2 2
4
AC a IH
2 2 2
16 4
BIK
có
BK R IK a IK
2 2 2 2 2
4
BD a IK
2 2 2
16 4
IHMK là hình chữ nhật (3 góc vuông)
IH IK IM = a
2 2 2 2

AC BD a IH IK a a a
2 2 2 2 2 2 2 2
32 4 32 4 28
ABCD
AC + BD a
S = AC.BD a
2 2 2 2
1 28 7
2 4 4
ABCD
Max S a2
7
khi
AC = BD
và hai dây cách tâm I một khoảng
IH = IK = a
2
2
ậy :
ABCD
Max S a2
7
.
--- Hết ---