S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ K THI TUY N SINH L P 10 THPT(2009-2010)Ỳ Ể Ớ
BÌNH ĐNHỊ
--------------------- MÔN: TOÁN
Th i gian: 120 phút ờ(không k th i gian phát đ)ể ờ ề
Bài 1. (2,0 đi m)ể Rút g n các bi u th c sau :ọ ể ứ
a)
2 3 3 27 300+ −
b)
1 1 1
:
1 ( 1)x x x x x
� �
+
� �
− − −
� �
Bài 2. (1,5 đi m)ể
a). Gi i ph ng trình: xả ươ 2 + 3x – 4 = 0
b) Gi i h ph ng trình: 3x – 2y = 4ả ệ ươ
2x + y = 5
Bài 3. (1,5 đi m)ể
Cho hàm s : y = (2m – 1)x + m + 1 v i m là tham s và m # ố ớ ố
1
2
. Hãy xác đnh m trong m iị ỗ
tr ng h p sau :ườ ơ
a) Đ th hàm s đi qua đi m M ( -1;1 )ồ ị ố ể
b) Đ th hàm s c t tr c tung, tr c hoành l n l t t i A , B sao cho tam giác OAB cân.ồ ị ố ắ ụ ụ ầ ượ ạ
Bài 4. (2,0 đi m): Gi i bài toán sau b ng cách l p ph ng trình ho c h ph ng trình:ể ả ằ ậ ươ ặ ệ ươ
M t ca nô chuy n đng xuôi dòng t b n A đn b n B sau đó chuy n đng ng c dòngộ ể ộ ừ ế ế ế ể ộ ượ
t B v A h t t ng th i gian là 5 gi . Bi t quãng đng sông t A đn B dài 60 Km và v n t cừ ề ế ổ ờ ờ ế ườ ừ ế ậ ố
dòng n c là 5 Km/h . Tính v n t c th c c a ca nô (( V n t c c a ca nô khi n c đng yên )ướ ậ ố ự ủ ậ ố ủ ướ ứ
Bài 5. (3,0 đi m)ể
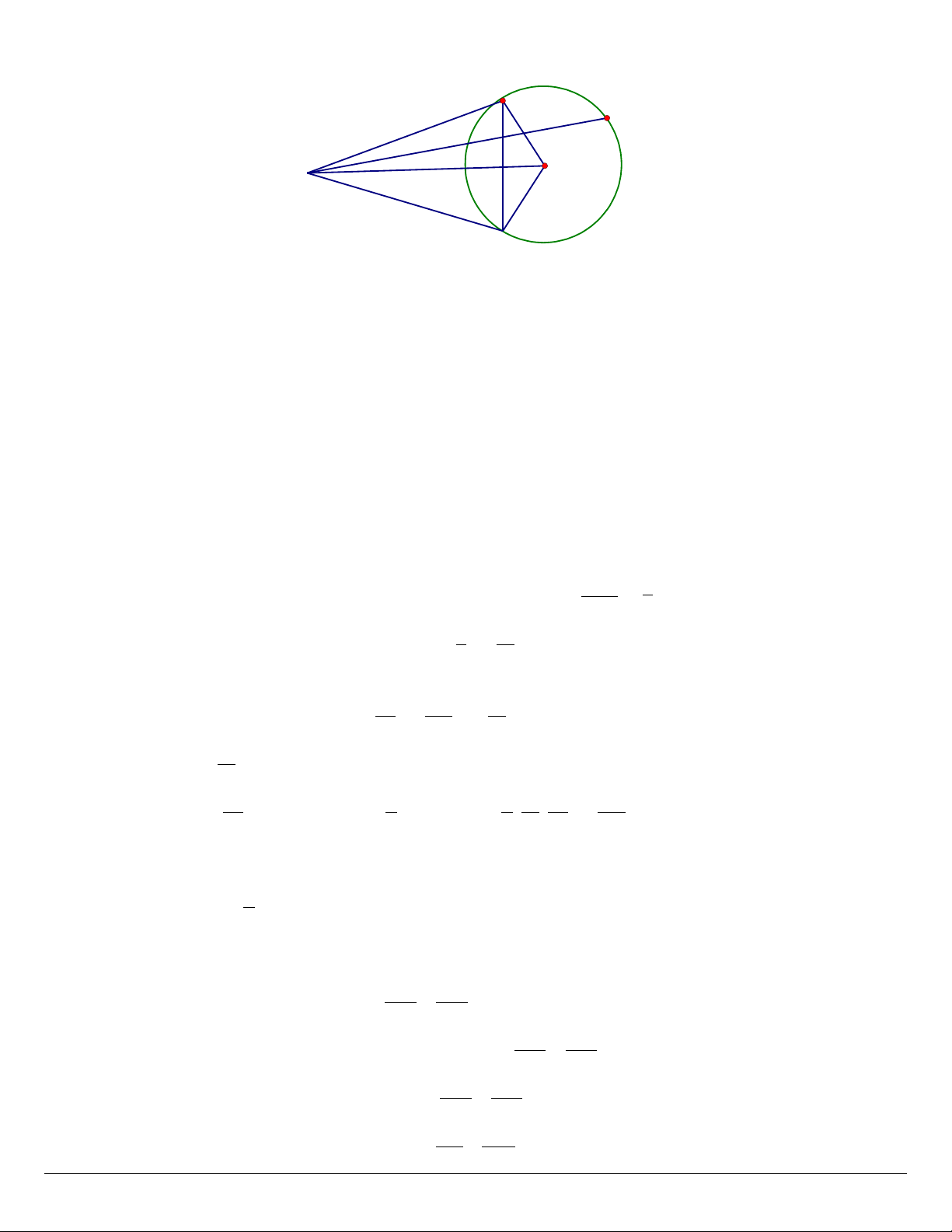
Cho đi m M n m ngoài đng tròn (O;R). T M k hai ti p tuy n MA , MB đn đngể ằ ườ ừ ẻ ế ế ế ườ
tròn (O;R) ( A; B là hai ti p đi m).ế ể
a) Ch ng minh MAOB là t giác n i ti p.ứ ứ ộ ế
b) Tính di n tích tam giác AMB n u cho OM = 5cm và R = 3 cm.ệ ế
c) K tia Mx n m trong góc AMO c t đng tròn (O;R) t i hai đi m C và D ( C n m gi aẻ ằ ắ ườ ạ ể ằ ữ
M và D ). G i E là giao đi m c a AB và OM. Ch ng minh r ng EA là tia phân giác c aọ ể ủ ứ ằ ủ
góc CED.
---------------------- H t ----------------------ế
(Cán b coi thi không gi i thích gì thêm)ộ ả
H và tên thí sinh: ……………………………………. ọS báo danh: ……………….ố
§¸p ¸n
Bµi 1:
a) A =
3
b) B = 1 +
x
Bµi 2 :
a) x1 = 1 ; x2 = -4
b) 3x – 2y = 4
2x + y = 5
<=> 3x – 2y = 4 7x = 14 x = 2
<=> <=>
4x + 2y = 5 2x + y = 5 y = 1
Bµi 3 :
a) V× ®å thÞ hµm sè ®i qua ®iÓm M(-1;1) => Täa ®é ®iÓm M ph¶i tháa m·n hµm sè :
y = (2m – 1)x + m + 1 (1)
Thay x = -1 ; y = 1 vµo (1) ta cã: 1 = -(2m -1 ) + m + 1
<=> 1 = 1 – 2m + m + 1
<=> 1 = 2 – m
<=> m = 1
VËy víi m = 1 Th× §T HS : y = (2m – 1)x + m + 1 ®i qua ®iÓm M ( -1; 1)
c) §THS c¾t trôc tung t¹i A => x = 0 ; y = m+1 => A ( 0 ; m+1) => OA =
1m+
c¾t truc hoµnh t¹i B => y = 0 ; x =
1
2 1
m
m
− −
−
=> B (
1
2 1
m
m
− −
−
; 0 ) => OB =
1
2 1
m
m
− −
−
Tam gi¸c OAB c©n => OA = OB
<=>
1m+
=
1
2 1
m
m
− −
−
Gi¶i PT ta cã : m = 0 ; m = -1
Bµi 4: Gäi vËn tèc thùc cña ca n« lµ x ( km/h) ( x>5)
VËn tèc xu«i dßng cña ca n« lµ x + 5 (km/h)
VËn tèc ngîc dßng cña ca n« lµ x - 5 (km/h)
Thêi gian ca n« ®i xu«i dßng lµ :
( giê)
Thêi gian ca n« ®i xu«i dßng lµ :
( giê)
Theo bµi ra ta cã PT:
+
= 5
<=> 60(x-5) +60(x+5) = 5(x2 – 25)
<=> 5 x2 – 120 x – 125 = 0
x1 = -1 ( kh«ng TM§K)
x2 = 25 ( TM§K)
VËy v©n tèc thùc cña ca n« lµ 25 km/h.
Bµi 5:
D
C
E
O
M
A
B
a) Ta cã: MA
⊥
AO ; MB
⊥
BO ( T/C tiÕp tuyÕn c¾t nhau)
=>
ﾷ ﾷ
0
90MAO MBO= =
Tø gi¸c MAOB cã :
ﾷ ﾷ
MAO MBO+ =
900 + 900 = 1800 => Tø gi¸c MAOB néi tiÕp ®êng trßn
b) ¸p dông §L Pi ta go vµo
∆
MAO vu«ng t¹i A cã: MO2 = MA2 + AO2
MA2 = MO2 – AO2
MA2 = 52 – 32 = 16 => MA = 4 ( cm)
V× MA;MB lµ 2 tiÕp tuyÕn c¾t nhau => MA = MB =>
∆
MAB c©n t¹i A
MO lµ ph©n gi¸c ( T/C tiÕp tuyÕn) = > MO lµ ®êng trung trùc => MO
⊥
AB
XÐt
∆
AMO vu«ng t¹i A cã MO
⊥
AB ta cã:
AO2 = MO . EO ( HTL trong
∆
vu«ng) => EO =
=
9
5
(cm)
=> ME = 5 -
9
5
=
16
5
(cm)
¸p dông §L Pi ta go vµo tam gi¸c AEO vu«ng t¹i E ta cã:AO2 = AE2 +EO2
AE2 = AO2 – EO2 = 9 -
81
25
=
144
25
=
12
5
AE =
12
5
( cm) => AB = 2AE (v× AE = BE do MO lµ ®êng trung trùc cña AB)
AB =
24
5
(cm) => SMAB =
1
2
ME . AB =
1 16 24
. .
2 5 5
=
192
25
(cm2)
c) XÐt
∆
AMO vu«ng t¹i A cã MO
⊥
AB. ¸p dông hÖ thøc lîng vµo tam gi¸c vu«ng AMO ta cã:
MA2 = ME. MO (1)
mµ :
ﾷ
ﾷ
ADC MAC=
=
1
2
S®
ﾷ
AC
( gãc néi tiÕp vµ gãc t¹o bëi tiÕp tuyÕn vµ d©y cung cïng ch¾n
1 cung)
∆
MAC
:
∆
DAM (g.g) =>
MA MD
MC MA
=
=> MA2 = MC . MD (2)
Tõ (1) vµ (2) => MC . MD = ME. MO =>
MD ME
MO MC
=
∆
MCE
:
∆
MDO ( c.g.c) (
ﾷ
M
chung;
MD ME
MO MC
=
) =>
ﾷ
ﾷ
MEC MDO=
( 2 gãc tøng) ( 3)
T¬ng tù:
∆
OAE
:
OMA (g.g) =>
OA
OE
=
OM
OA
=>
OA
OE
=
OM
OA
=
OD OM
OE OD
=
( OD = OA = R)
Ta cã:
∆
DOE
:
∆
MOD ( c.g.c) (
ﾷ
O
chong ;
OD OM
OE OD
=
) =>
ﾷ
ﾷ
OED ODM=
( 2 gãc t øng) (4)
Tõ (3) (4) =>
ﾷ
ﾷ
OED MEC=
. mµ :
ﾷ
ﾷ
AEC MEC+
=900
ﾷ ﾷ
AED OED+
=900
=>
ﾷ
ﾷ
AEC AED=
=> EA lµ ph©n gi¸c cña