S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ
HA TINH
KÌ THI TUY N SINH L P 10 THPT Ể Ớ
NĂM H C 2013- 2014Ọ
Môn thi: TOÁN (không chuyên)
Th i gian làm bài: 120 phútờ
Ngày thi 19 tháng 6 năm 2013
Đ thi g m : 01 trangề ồ
Câu I (2,0 đi m)ể
1) Gi i ph ng trình (2x + 1)ả ươ 2 + (x – 3)2 = 10
2) Xác đ nh các h s m và n bi t h ph ng trình ị ệ ố ế ệ ươ
3 5
2 9
x my
mx ny
− =
+ =
có nghi m (1;ệ
-2)
Câu II ( 2,0 đi m)ể
1) Rút g n bi u th c ọ ể ứ
2 3 1 1
A= +
x +1 x- 1 x 1
x x x
x x
− + − −
+ +
v i ớ
x 0
2) Hai ng i th quét s n m t ngôi nhà. N u h cùng làm thì trong 6 ngày xongườ ợ ơ ộ ế ọ
vi c. N u h làm riêng thì ng i th th nh t hoàn thành công vi c ch m h n ng iệ ế ọ ườ ợ ứ ấ ệ ậ ơ ườ
th th hai là 9 ngày. H i n u làm riêng thì m i ng i th ph i làm trong bao nhiêuợ ứ ỏ ế ỗ ườ ợ ả
ngày đ xong vi c.ể ệ
Câu III (2,0 đi m)ể
Cho ph ng trình ươ
2
2( 1) 2 5 0x m x m− − + − =
1) Ch ng minh r ng ph ng trình luôn có hai nghi m xứ ằ ươ ệ 1; x2 v i m i m.ớ ọ
2) Tìm các giá tr c a m đ ph ng trình có hai nghi m xị ủ ể ươ ệ 1; x2 th a mãn đi uỏ ề
ki n:ệ
2 2
1 1 2 2
( 2 2 1)( 2 2 1) 0x mx m x mx m− + − − + − <
Câu IV (3,0 đi m)ể
Cho ba đi m A, B, C c đ nh và th ng hàng theo th t đó. Đ ng tròn (O; R) thayể ố ị ẳ ứ ự ườ
đ i đi qua B và C sao cho O không thu c BC. T đi m A v hai ti p tuy n AM và ANổ ộ ừ ể ẽ ế ế
v i đ ng tròn (O). G i I là trung đi m c a BC, E là giao đi m c a MN và BC, H làớ ườ ọ ể ủ ể ủ
giao đi m c a đ ng th ng OI và đ ng th ng MN.ể ủ ườ ẳ ườ ẳ
1) Ch ng minh b n đi m M, N, O, I cùng thu c m t đ ng tròn.ứ ố ể ộ ộ ườ
2) Ch ng minh OI.OH = Rứ2.
3) Ch ng minh đ ng th ng MN luôn đi qua m t đi m c đ nh.ứ ườ ẳ ộ ể ố ị
Câu V ( 1,0 đi m)ể
Cho tam giác ABC có chu vi b ng 2. Ký hi u a, b, c là đ dài ba c nh c a tamằ ệ ộ ạ ủ
giác. Tìm giá tr nh nh t c a bi u th c ị ỏ ấ ủ ể ứ
4 9a b c
Sb c a c a b a b c
= + +
+ − + − + −
.
----------------------- H t ----------------------ế
H và tên thí sinhọ : ................................................ S báo danh ...................................ố..
Ch ký c a giám th 1 ........................................... Ch ký c a giám thữ ủ ị ữ ủ ị
2 ..........................
Đ THI CHÍNH TH CỀ Ứ
H ng d n câu ướ ẫ III:
2) ph ng trình có hai nghi m xươ ệ 1; x2 nên
2 2
1 1 1 1 1
2 2
2 2 2 2 2
x 2(m 1)x 2m 5 0 x 2mx 2m 1 4 2x
x 2(m 1)x 2m 5 0 x 2mx 2m 1 4 2x
� �
− − + − = − + − = −
� �
� �
− − + − = − + − = −
� �
� �
Theo đ nh lí Vi-et ta cóị :
Theo bài ra ta có :
( ) ( )
( )
( ) ( )
2 2
1 1 2 2
1 2
1 2 1 2
(x 2mx 2m 1)(x 2mx 2m 1) 0
4 2x . 4 2x 0
16 8 x x 4x x 0
16 8 2m 2 4 2m 5 0
3
m2
− + − − + − <
− − <�
− + + <�
− − + − <�
>�
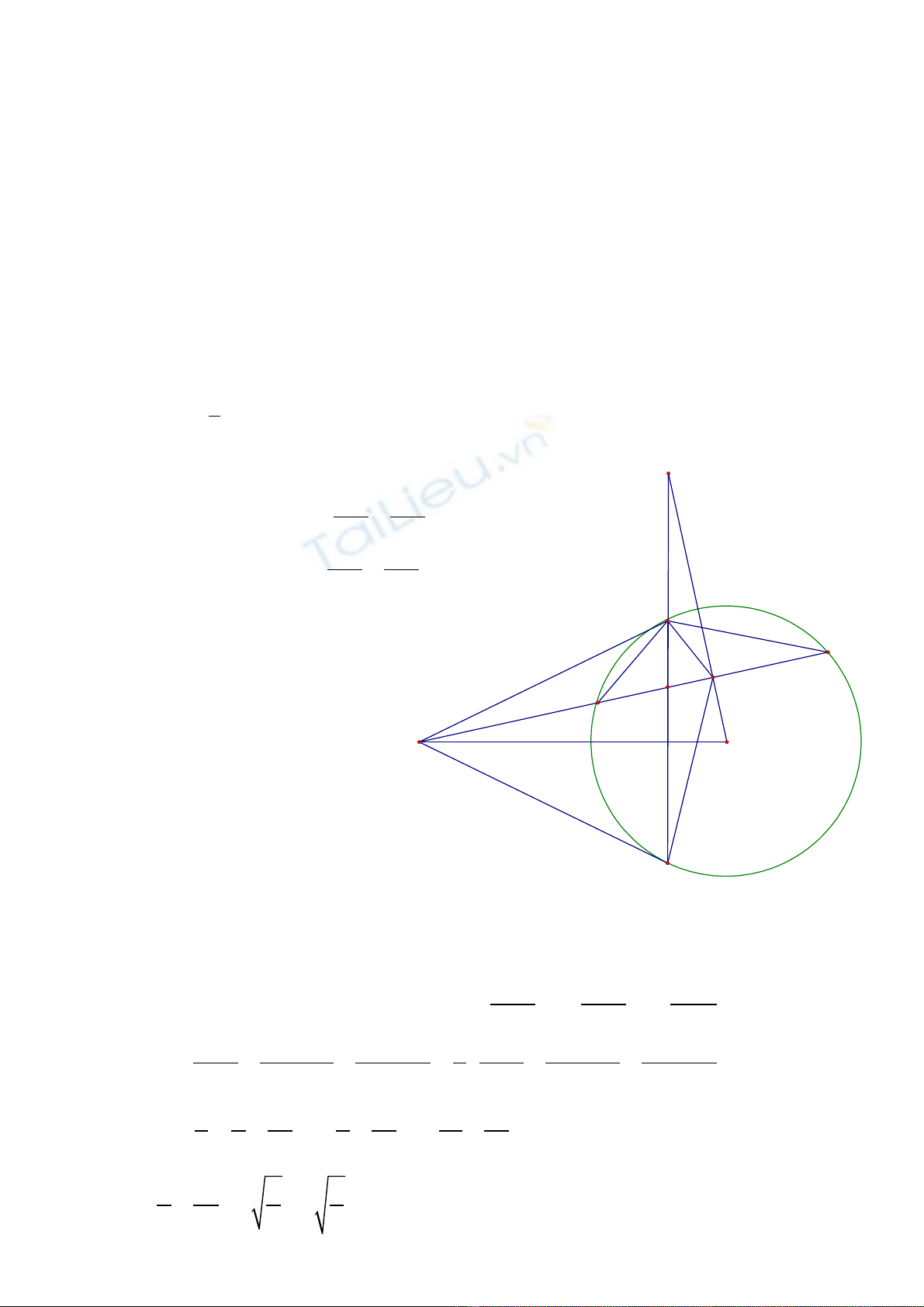
H ng d n câu ướ ẫ IVc :
+
AMB∆
∽
ACM∆
(g-g)
2
AM AB AM AB.AC
AC AM
= =�
+
AME∆
∽
AIM∆
(g-g)
2
AM AE AM AI.AE
AI AM
= =�
AB.AC = AI.AE (*)
Do A, B, C c đ nh nên trung đi m I c a BC c đ nhố ị ể ủ ố ị
nên t (*) suy ra E c đ nh.ừ ố ị
V y ậđ ng th ng MN luôn đi qua đi m E c đ nhườ ẳ ể ố ị
H ng d n gi i câu V:ướ ẫ ả
V i a, b, c là đ dài ba c nh c a tam giác có chu vi b ng 2 nên ớ ộ ạ ủ ằ
a b c 2
+ + =
.
Đ t ặ
b c a x; c a b y; a b c z
+ − = + − = + − =
do a, b, c là đ dài ba c nh c a tam giácộ ạ ủ
nên
x, y,z 0>
.
Suy ra
x y z 2+ + =
(do
a b c 2
+ + =
) và
y z x z x y
a ; b ; c
2 2 2
+ + +
= = =
.
Khi đó
( ) ( ) ( ) ( )
4 x z 9 x y 4 x z 9 x y
y z 1 y z
S2x 2y 2z 2 x y z
+ + + +� �
+ +
= + + = + +
� �
� �
1 y 4x z 9x 4z 9y
2 x y x z y z
� �
� � � �
� �
= + + + + +
� �
� �
� � � �
� �
� � � �
� �
Ta có:
2
y 4x y x
2 2 2
x y x y
� �
+ = − +
� �
� �
H
E
I
B
N
O
A
M
C
2
z 9x z x
3 6 6
x z x z
� �
+ = − +
� �
� �
2
4z 9y z y
2 3 12 12
y z y z
� �
+ = − +
� �
� �
( )
1
S 4 6 12 11
2
= + +
D u “=” x y ra khi ấ ả
1
x
y 2x 3
z 3x 2
y
2z 3y 3
z 1
x y z 2
=
=
=
� � =�
� �
=
� � =
� �
+ + =
5 2 1
a ; b ; c
6 3 2
= = =�
Khi đó:
2 2 2
a b c= +
ABC
∆�
vuông
V y ậ
min
S 11
=
ABC
∆
vuông
5 2 1
a ; b ; c
6 3 2
= = =
.