TR NG THPT CHUYÊNƯỜ
LÊ QUÝ ĐÔN
L n IIầ
http://ductam_tp.violet.vn/
Đ THI TH Đ I H C, CAO Đ NG NĂM 2011Ề Ử Ạ Ọ Ẳ
Môn thi: TOÁN, kh i A, Bố
Th i gian làm bài 180 phút, không k th i gian giao đờ ể ờ ề
Câu I: (2,0 đi m)ể
Cho hàm s ố
2 4 ( )
1
x
y C
x
−
=+
.
1. Kh o sát s bi n thiên và v đ th (C) c a hàm s .ả ự ế ẽ ồ ị ủ ố
2. G i M là m t đi m b t kì trên đ th (C), ti p tuy n t i M c t các ti m c n c a (C) t iọ ộ ể ấ ồ ị ế ế ạ ắ ệ ậ ủ ạ
A, B. CMR di n tích tam giác ABI (I là giao c a hai ti m c n) không ph thu c vào v tríệ ủ ệ ậ ụ ộ ị
c a M.ủ
Câu II: (3,0 đi m)ể
1. Gi i h ph ng trình:ả ệ ươ
2 2
2
21
xy
x y x y
x y x y
+ + =
+
+ = −
2. Gi i ph ng trình: ả ươ
2 2
2sin 2sin t anx
4
x x
π
− = −
÷
.
3. Gi i b t ph ng trình: ả ấ ươ
( ) ( )
2 2
1 5 3 1
3 5
log log 1 log log 1x x x x+ + > + −
Câu III: (2,0 đi m)ể
1. Tính tích phân:
2
3
1
ln 2 ln
ex x
I dx
x
+
=
∫
.
2. Cho t p ậ
{ }
0;1;2;3;4;5A
=
, t A có th l p đ c bao nhiêu s t nhiên g m 5 ch sừ ể ậ ượ ố ự ồ ữ ố
khác nhau, trong đó nh t thi t ph i có ch s 0 và 3.ấ ế ả ữ ố
Câu IV: (2,0 đi m)ể
1. Vi t ph ng trình đ ng tròn đi qua hai đi m A(2; 5), B(4;1) và ti p xúc v i đ ngế ươ ườ ể ế ớ ườ
th ng có ph ng trình 3x – y + 9 = 0.ẳ ươ
2. Cho hình lăng tr tam giác ABC.A’B’C’ v i A’.ABC là hình chóp tam giác đ u c nh đáyụ ớ ề ạ
AB = a; c nh bên AA’ = b. G i ạ ọ
α
là góc gi a hai mp(ABC) và mp(A’BC). Tính ữ
tan
α
và
th tích chóp A’.BCC’B’.ể
Câu V: (1,0 đi m)ể
Cho
. Tìm giá tr nh nh t c a bi u th cị ỏ ấ ủ ể ứ
1 1
x y
Tx y
= +
− −
……………………………………………….H t………………………………………………….ế
ĐÁP ÁN Đ THI TH Đ I H C L N 2 A, B NĂM 2011Ề Ử Ạ Ọ Ầ
Câu Ý N i dungộĐiể
m
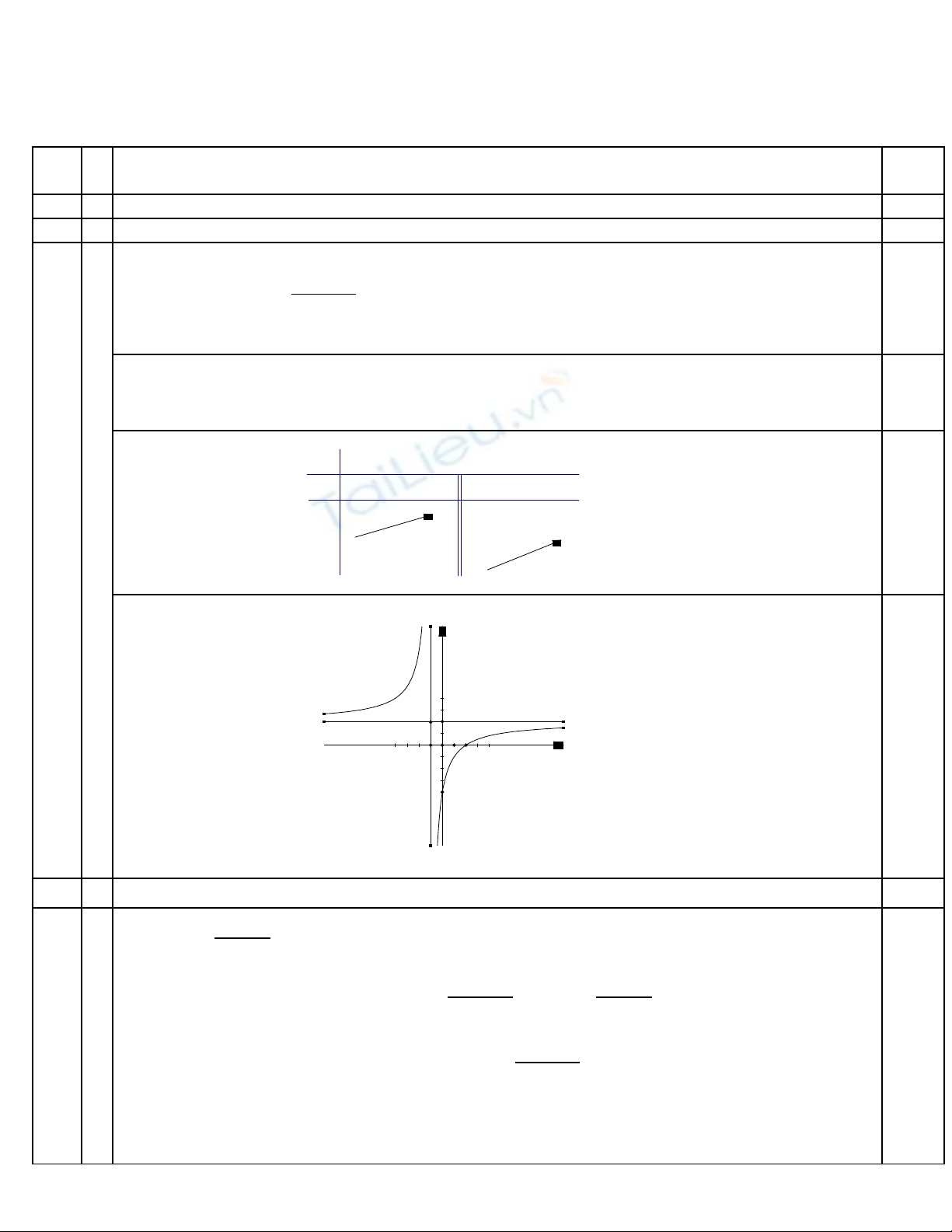
I 2
1 Kh o sát s bi n thiên và v đ th (C) c a hàm s (1,00 đi m)ả ự ế ẽ ồ ị ủ ố ể
-T p xác đ nh: R\{-1}ậ ị
-S bi n thiên: ự ế
( )
2
6
' 0 1
1
y x
x
= > ∀ ≠ −
+
. Suy ra hàm s đ ng bi n trên các kho ng xácố ồ ế ả
đ nh c a hàm s .ị ủ ố
0.25
-
( )
1
lim 1
x
y x
±
→ −
= ∞ → = −
m
là ti m c n đ ngệ ậ ứ
-
lim 2 2
xy y
→±∞ = → =
là ti m c n ngangệ ậ 0.25
-B ng bi n thiênả ế
0.25
-Đ thồ ị
0.25
2 Tìm c p đi m đ i x ng….(1,00 đi m)ặ ể ố ứ ể
G i ọ
( )
2 4
; 1
1
a
M a C a
a
−
∈ ≠ −
÷
+
Ti p tuy n t i M có ph ng trình: ế ế ạ ươ
( ) ( )
2
6 2 4
1
1
a
y x a a
a
−
= − + +
+
Giao đi m v i ti m c n đ ng ể ớ ệ ậ ứ
1x= −
là
2 10
1; 1
a
Aa
−
−
÷
+
Giao đi m v i ti m c n ngang ể ớ ệ ậ
2y=
là
( )
2 1;2B a +
Giao hai ti m c n I(-1; 2)ệ ậ
0.25
0.25
0.25
0.25
-
∞
+
∞
2
2
+
+
-1
+
∞
-
∞
y
y'
x
x
y
2
-1
-4
2
1
I
( ) ( )
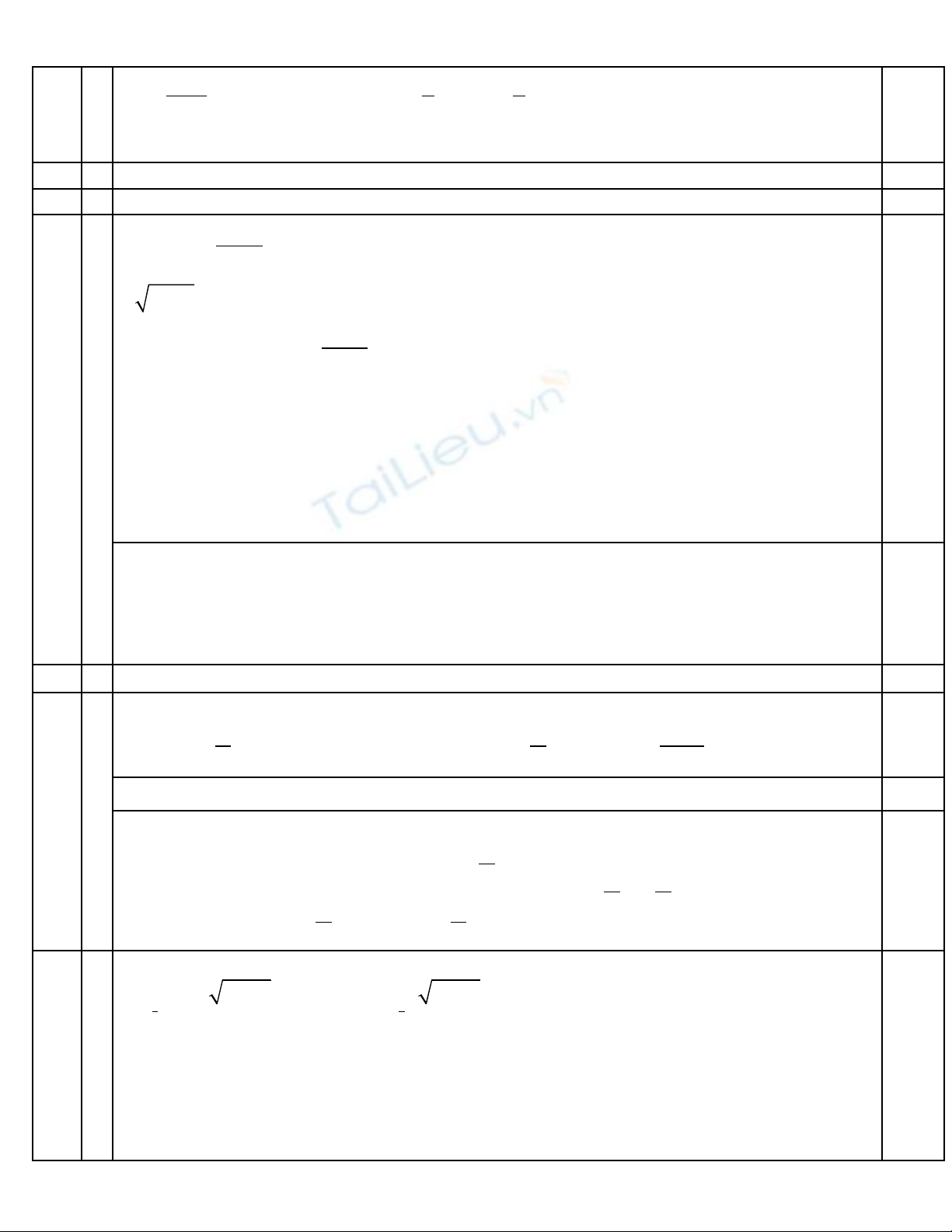
12 1 1
; 2 1 . .24 12
1 2 2
IAB
IA IB a S IA AB dvdt
a
= = + ⇒ = = =
+
Suy ra đpcm
II 3
1 Gi i h …(1,00 đi m)ả ệ ể
( )
( ) ( )
2 2
2
21 1 0
2
xy
x y x y dk x y
x y x y
+ + =
++ >
+ = −
( ) ( ) ( ) ( ) ( )
2 3
2
1 2 1 0 2 2 0
xy
x y xy x y xy x y xy x y
x y
⇔ + − + − = ⇔ + − + + − + =
+
( ) ( )
( )
( )
( ) ( ) ( )
( ) ( )
2
2 2
1 2 1 0
1 1 2 0
1 3
0 4
x y x y xy x y
x y x y x y xy
x y
x y x y
⇔ + + − − + − =
⇔ + − + + + − =
+ =
⇔+ + + =
0.5
D th y (4) vô nghi m vì x+y>0ễ ấ ệ
Th (3) vào (2) ta đ c ế ượ
2
1x y
− =
Gi i h ả ệ
2
11; 0
2; 3
1
x y x y
x y
x y
+ = = =
⇒
= − =
− =
……
0.5
2 Gi i ph ng trình….(1,00 đi m)ả ươ ể
Đk:
cos 0x
≠
(*)
2 2 2
sinx
2sin 2sin tanx 1 cos 2 2sin
4 2 cos
x x x x x
π π
− = − ⇔ − − = −
÷ ÷
0.25
( )
2
cos sin 2 .cos 2sin .cos sinx cos sinx sin 2 cos sinx 0x x x x x x x x
⇔ − − + ⇔ + − + =
0.25
cos 0
sinx cos t anx 1 4
4 2
sin 2 1 2 2
2 4
x
x x k
x k
x x l x l
πππ π
π π
π π
≠
= − → = − ⇔ = − +
⇔ → = +
= ⇔ = + ⇔ = +
(tm(*))… 0.5
3 Gi i b t ph ng trình (1,00 đi m)ả ấ ươ ể
( ) ( )
2 2
1 5 3 1
3 5
log log 1 log log 1 (1)x x x x+ + > + −
Đk:
0x>
0.25
( )
( ) ( )
( ) ( )
( )
2 2
3 1 3 5
5
2 2
3 1 5
5
2 2
5
1 log log 1 log log 1 0
log log 1 .log 1 0
log 1 1
x x x x
x x x x
x x
⇔ + − + + + <
⇔ + − + + <
÷
⇔ + + <
( )
2
5
0 log 1 1x x
⇔ < + + <
*)
( )
2
5
0 log 1 0x x x
< + + ⇔ >
*)
( )
2 2 2
5
12
log 1 1 1 5 1 5 ... 5
x x x x x x x
+ + < ⇔ + + < ⇔ + < − ⇔ ⇔ <
V y BPT có nghi m ậ ệ
12
0; 5
x
∈ ÷
0.25
0.25
0.2
III 2
1 Tính tích phân (1,00 đi m)ể
( )
( ) ( )
( )
2
31
2 2 2
33
1 1 1
4
2
3
4 4
3
3
1
ln 2 ln 1
ln 2 ln ln 2 ln 2 ln
2
3 2 ln
1 3
. 3 2
2 4 8
e e e
e
x x
I dx x xd x x d x
x
x
+
= = + = + +
+
= = −
∫ ∫ ∫
0.5
0.5
2 L p s …..(1,00 đi m)ậ ố ể
-G i s c n tìm là ọ ố ầ
( )
0abcde a ≠
-Tìm s các s có 5 ch s khác nhau mà có m t 0 và 3 không xét đ n v trí a.ố ố ữ ố ặ ế ị
X p 0 và 3 vào 5 v trí có: ế ị
2
5
A
cách
3 v trí còn l i có ị ạ
3
4
A
cách
Suy ra có
2 3
5 4
A A
s ố
-Tìm s các s có 5 ch s khác nhau mà có m t 0 và 3 v i a = 0.ố ố ữ ố ặ ớ
X p 3 có 4 cáchế
3 v trí còn l i có ị ạ
3
4
A
cách
Suy ra có
3
4
4.A
số
V y s các s c n tìm tmycbt là: ậ ố ố ầ
2 3
5 4
A A
-
3
4
4.A
= 384
0.25
0.25
0.25
0.25
IV 2
1 Vi t ph ng trình đ ng tròn….(1,00 đi m)ế ươ ườ ể
G i ọ
( )
;I a b
là tâm đ ng tròn ta có hườ ệ
( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
2 2 2 2
2
2 2
2 5 4 1 (1)
3 9
;2 5 2
10
a b a b
IA IB
a b
IA d I a b
− + − = − + −
=
⇔
− +
= ∆
− + − =
( )
1 2 3a b
⇔ = −
th vào (2) ta có ế
212 20 0 2 10b b b b
− + = ⇔ = ∨ =
*) v i ớ
( ) ( ) ( )
2 2
2 1; 10 : 1 2 10b a R C x y= ⇒ = = ⇒ − + − =
*)v i ớ
( ) ( ) ( )
2 2
10 17; 250 : 17 10 250b a R C x y= ⇒ = = ⇒ − + − =
0.25
0.25
0.25
0.25
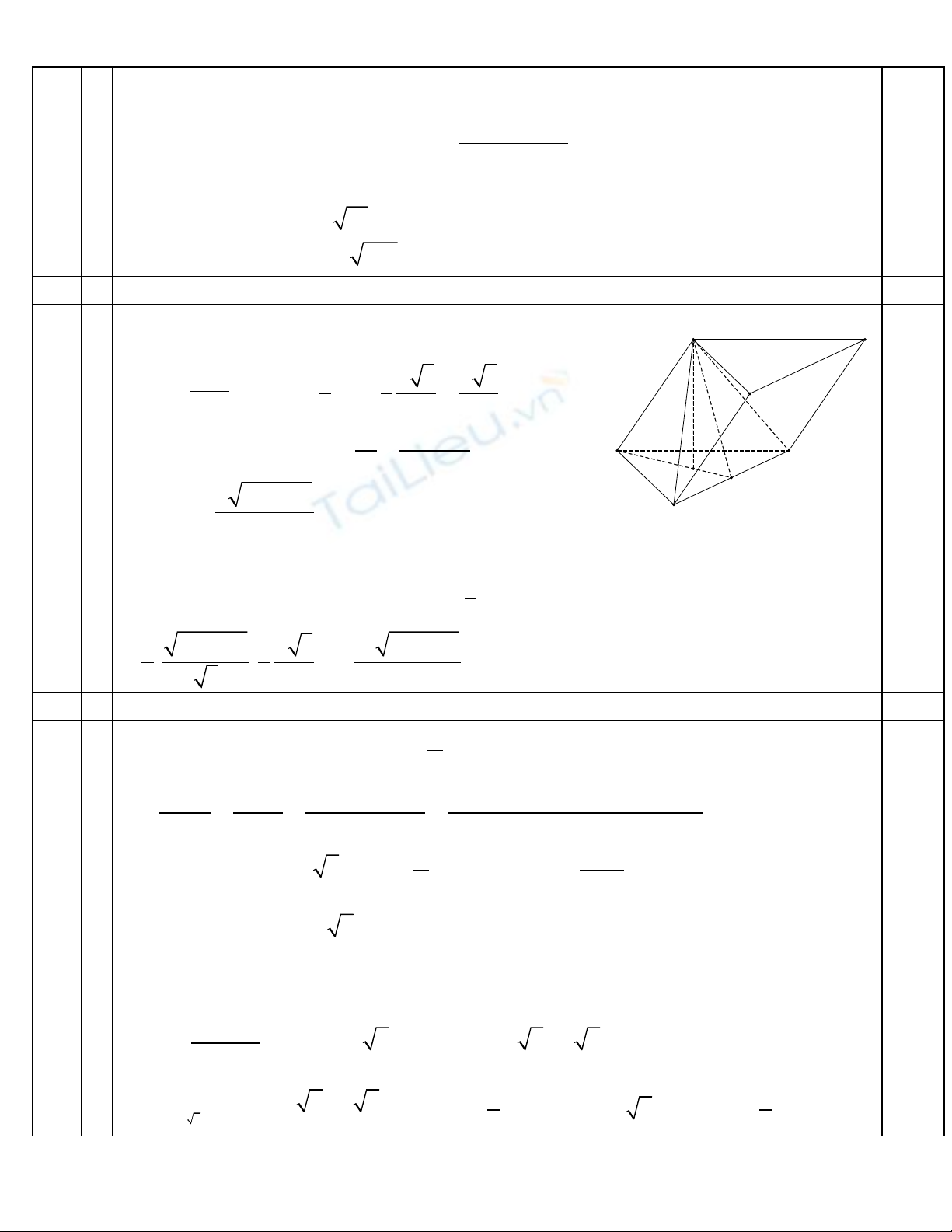
2 Hình lăng tr ….(1,00 đi m)ụ ể
G i O là tâm đáy suy ra ọ
( )
'A O ABC
⊥
và góc
·
'AIA
α
=
*)Tính
tan
α
'
tan A O
OI
α
=
v i ớ
1 1 3 3
3 3 2 6
a a
OI AI= = =
2 2 2
2 2 2 2 3
' ' 3 3
a b a
A O A A AO b −
= − = − =
2 2
2 3
tan b a
a
α
−
⇒ =
*)Tính
'. ' 'A BCC B
V
( )
'. ' ' . ' ' ' '.
2 2 2 2 2
1
' . ' .
3
2 3 1 3 3
. . .
3 2 2 6
3
A BCC B ABC A B C A ABC ABC ABC
V V V A O S A O S
b a a a b a
a dvtt
= − = −
− −
= =
0.25
0.25
0.5
V1
Đ t ặ
2 2
cos ; sin 0; 2
x a y a a
π
= = ⇒ ∈ ÷
khi đó
( ) ( )
2 2 3 3 sin cos 1 sin .cos
cos sin cos sin
sin cos sina.cos sin .cos
a a a a
a a a a
Ta a a a a
+ −
+
= + = =
Đ t ặ
21
sin cos 2 sin sin .cos
4 2
t
t a a a a a
π
−
= + = + ⇒ =
÷
V i ớ
0 1 2
2
a t
π
< < ⇒ < ≤
Khi đó
( )
3
2
3
1
t t
T f t
t
− −
= =
−
;
( )
( )
(
( )
( )
4
2
2
3
' 0 1; 2 2 2
1
t
f t t f t f
t
− −
= < ∀ ∈ ⇒ ≥ =
−
V y ậ
(
( )
( )
1; 2
min 2 2
t
f t f
∈
= =
khi
1
2
x y
= =
. Hay
min 2T
=
khi
1
2
x y
= =
.
I
B'
C'
O
A
C
B
A'