Đ THI TH Đ I H C, CAO Đ NG NĂM 2011Ề Ử Ạ Ọ Ẳ
Môn thi: TOÁN, kh i A, Bố
Th i gian làm bài 180 phút, không k th i gian giao đờ ể ờ ề
Câu 1 (2.0 đi m): ể Cho hàm s ố
3 2 3
3 4y x mx m= − +
(m là tham s ) có đ th là (Cố ồ ị m)
1. Kh o sát và v đ th hàm s khi ả ẽ ồ ị ố m = 1.
2. Xác đ nh ịm đ (Cểm) có các đi m c c đ i và c c ti u đ i x ng nhau qua đ ngể ự ạ ự ể ố ứ ườ
th ng ẳy = x.
Câu 2 (2.0 đi m ) :ể
1. Gi i ph ng trình:ả ươ
2
3 4 2sin 2 2 3 2(cotg 1)
sin 2
cos
xx
x
x
+
+ − = +
.
2. Tìm m đ h ph ng trình: ể ệ ươ
3 3 2
2 2 2
3 3 2 0
1 3 2 0
x y y x
x x y y m
− + − − =
+ − − − + =
có nghi m th c.ệ ự
Câu 3 (2.0 đi m):ể 2. Trong không gian v i h t a đ ớ ệ ọ ộ Oxyz, cho m t ph ng (ặ ẳ P) và
đ ng th ng (ườ ẳ d) l n l t có ph ng trình:ầ ượ ươ
(P): 2x − y − 2z − 2 = 0; (d):
1 2
1 2 1
x y z+ −
= =
−
1. Vi t ph ng trình m t c u có tâm thu c đ ng th ng (ế ươ ặ ầ ộ ườ ẳ d), cách m t ph ng (ặ ẳ P)
m t kho ng b ng 2 và c t m t ph ng (ộ ả ằ ắ ặ ẳ P) theo giao tuy n là đ ng tròn có bán kínhế ườ
b ng 3.ằ
2. Vi t ph ng trình m t ph ng (ế ươ ặ ẳ Q) ch a đ ng th ng (ứ ườ ẳ d) và t o v i m t ph ngạ ớ ặ ẳ
(P) m t góc nh nh t.ộ ỏ ấ
Câu 4 (2.0 đi m):ể
1. Cho parabol (P): y = x2. G i (ọd) là ti p tuy n c a (ế ế ủ P) t i đi m có hoành đ ạ ể ộ x = 2.
G i (ọH) là hình gi i h n b i (ớ ạ ở P), (d) và tr c hoành. Tính th tích v t th tròn xoayụ ể ậ ể
sinh ra b i hình (ởH) khi quay quanh tr c ụOx.
2. Cho x, y, z là các s th c d ng th a mãn: ố ự ươ ỏ x2 + y2 + z2 ≤ 3. Tìm giá tr nh nh tị ỏ ấ
c a bi u th c: ủ ể ứ
1 1 1
111
Pxy yz zx
=++
+++
Câu 5 (2.0 đi m)ể:
1. Trong m t ph ng v i h t a đ ặ ẳ ớ ệ ọ ộ Oxy, hãy l p ph ng trình ti p tuy n chung c aậ ươ ế ế ủ
elip (E):
2 2
1
8 6
x y
+ =
và parabol (P): y2 = 12x.
2. Tìm h s c a s h ng ch a ệ ố ủ ố ạ ứ x8 trong khai tri n Newton: ể
12
41
1xx
− −
÷
−−−−−−−−−−−−−o0o−−−−−−−−−−−−−
Cán b coi thi không gi i thích gì thêm.ộ ả
H và tên thí sinh:....................................................................SBD:......................ọ
Câu N i dungộĐiể
m
I1. Khi m = 1, hàm s có d ng: ố ạ y = x3 − 3x2 + 4
+ TXĐ: R
+ S bi n thiên: ự ế y’ = 3x2 − 6x = 0 ⇔ x = 0 ho c ặx = 2
Hàm s đ ng bi n trên: (ố ồ ế −∞; 0) và (2; +∞)
Hàm s nghich bi n trên: (0; 2)ố ế
Hàm s đ t CĐ t i ố ạ ạ xCĐ = 0, yCĐ = 4; đ t CT t i ạ ạ xCT = 2, yCT = 0
y” = 6x − 6 = 0 ⇔ x = 1
Đ th hàm s l i trên (ồ ị ố ồ −∞; 1), lõm trên (1; +∞). Đi m u n (1; 2)ể ố
0.25
Gi i h n và ti m c n: ớ ạ ệ ậ
0.25
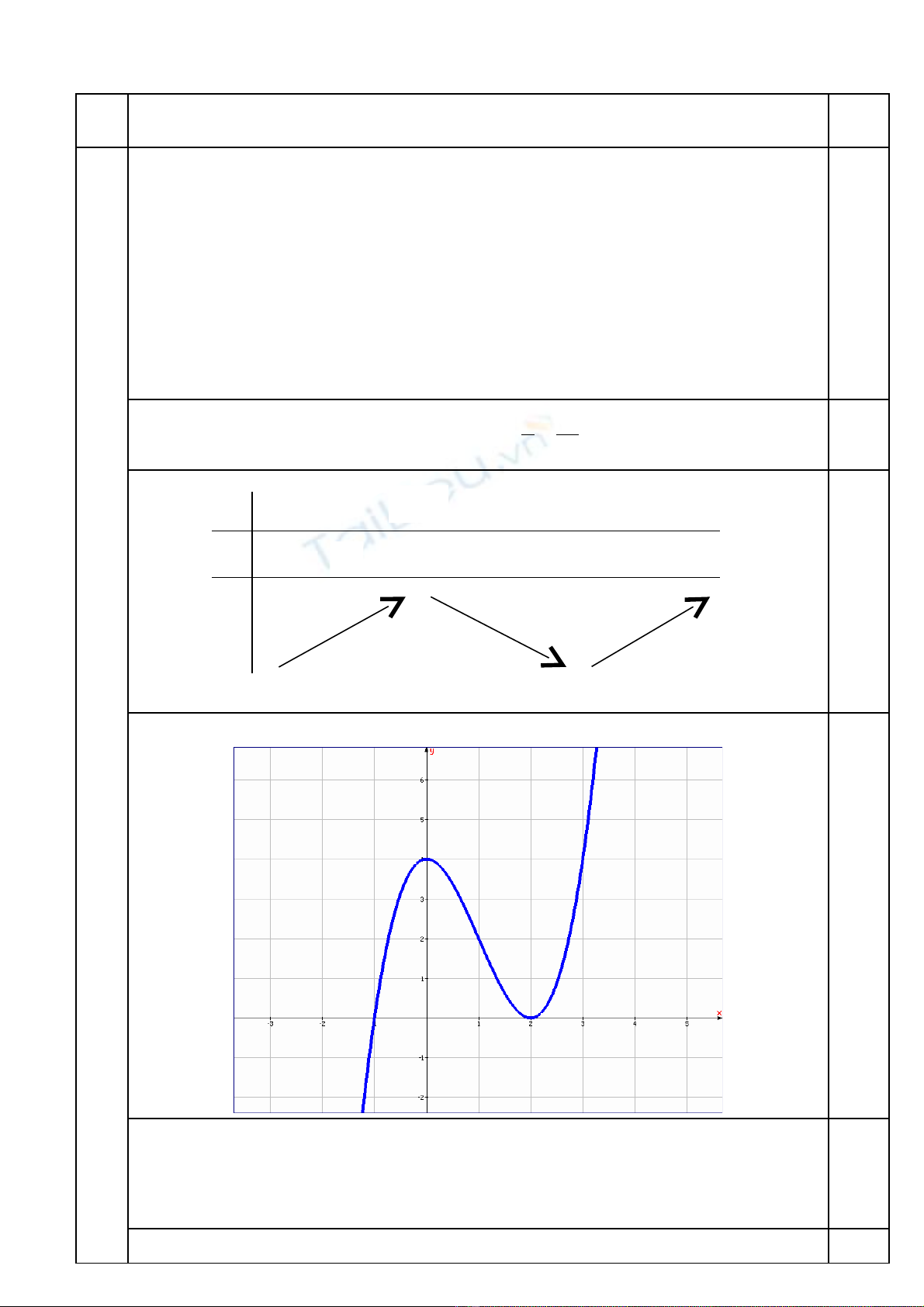
LËp BBT:
0.25
§å thÞ:
0.25
2/. Ta có: y’ = 3x2 − 6mx = 0 ⇔
0
2
x
x m
=
=
Đ hàm s có c c đ i và c c ti u thì ể ố ự ạ ự ể m ≠ 0.
0.25
Gi s hàm s có hai đi m c c tr là: ả ử ố ể ự ị A(0; 4m3), B(2m; 0) ⇒ 0.25
0
x
4+∞
−∞
−
++
00
y’
−∞ 2+∞
y
0
x
y
O
3
(2 ; 4 )AB m m= −
uuur
Trung đi m c a đo n ể ủ ạ AB là I(m; 2m3)
Đi u ki n đ ề ệ ể AB đ i x ng nhau qua đ ng th ng ố ứ ườ ẳ y = x là AB vuông góc v iớ
đ ng th ng ườ ẳ y = x và I thu c đ ng th ng ộ ườ ẳ y = x
3
3
2 4 0
2
m m
m m
− =
⇔=
0.25
Gi i ra ta có: ả
2
2
m= ±
; m = 0 0.25
K t h p v i đi u ki n ta có: ế ợ ớ ề ệ
2
2
m= ±
II
2/. Đk:
2
x k π
≠
0.25
Ph ng trình đã cho t ng đ ng v i:ươ ươ ươ ớ
( )
2
2 2
2
2
4
3 1 2 3 2
sin 2
2(sin cos )
3 3 2
sin cos
3 2 3 0
tg cotg
tg cotg
tg tg
x x
x
x x
x x
x x
x x
+ + − =
+
⇔ + − =
⇔ + − =
0.25
⇔
33
1
36
tg
tg
x k
x
xx k
π
= − + π
= −
⇔
π
== + π
0.25
KL: So sánh v i đi u ki n ph ng trình có nghi m : ớ ề ệ ươ ệ
6 2
x k
π π
= +
; k∈Z0.25
2/.
3 3 2
2 2 2
3 3 2 0 (1)
1 3 2 0 (2)
x y y x
x x y y m
− + − − =
+ − − − + =
Đi u ki n: ề ệ
2
2
1 0 1 1
0 2
2 0
x x
y
y y
− ≥ − ≤ ≤
⇔
≤ ≤
− ≥
0.25
Đ t ặt = x + 1 ⇒ t∈[0; 2]; ta có (1) ⇔ t3 − 3t2 = y3 − 3y2.0.25
Hàm s ốf(u) = u3 − 3u2 ngh ch bi n trên đo n [0; 2] nên: ị ế ạ
(1) ⇔ y = y ⇔ y = x + 1 ⇒ (2) ⇔
2 2
2 1 0x x m− − + =
0.25
Đ t ặ
2
1v x= −
⇒ v∈[0; 1] ⇒ (2) ⇔ v2 + 2v − 1 = m.
Hàm s ốg(v) = v2 + 2v − 1 đ t ạ
0;1 0;1
min ( ) 1; m ( ) 2
[ ] [ ]
axg v g v= − =
V y h ph ng trình có nghi m khi và ch khi ậ ệ ươ ệ ỉ −1 ≤ m≤ 2
0.25
III
1/. Đ ng th ng (ườ ẳ ∆) có ph ng trình tham s là: ươ ố
1 2 ;
2
x t
y t t R
z t
= −
= − + ∈
= +
G i tâm m t c u là ọ ặ ầ I. Gi s ả ử I(−t; −1 + 2t; 2+ t)∈(∆).
0.25
Vì tâm m t c u cách m t ph ng (ặ ầ ặ ẳ P) m t kho ng b ng 3 nên:ộ ả ằ
| 2 1 2 4 2 2 | | 6 5|
( ; ) 3
3 3
t t t t
d I − + − − − − +
∆ = = =
⇔
2
3
7
3
t
t
=
= −
0.25
⇒ Có hai tâm m t c u: ặ ầ
2 1 8 7 17 1
; ; ; ;
3 3 3 3 3 7
vµ I I
− − −
÷ ÷
Vì m t ph ng (ặ ẳ P) c t m t c u theo đ ng tròn có bán kính b ng 4 nên m tắ ặ ầ ườ ằ ặ
c u có bán kính là ầR = 5.
0.25
V y ph ng trình m t c u c n tìm là:ậ ươ ặ ầ ầ
2 2 2 2 2 2
2 1 8 7 17 1
25 25
3 3 3 3 3 3
vµ x y z x y z
+ + − + − = − + + + + =
÷ ÷ ÷ ÷ ÷ ÷
0.25
2/. Đ ng th ng (ườ ẳ ∆) có VTCP
( 1;2;1)u= −
r
; PTTQ:
2 1 0
2 0
x y
x z
+ + =
+ − =
M t ph ng (ặ ẳ P) có VTPT
(2; 1; 2)n= − −
r
0.25
Góc gi a đ ng th ng (ữ ườ ẳ ∆) và m t ph ng (ặ ẳ P) là:
| 2 2 2 | 6
sin 3
3. 6
− − −
α = =
⇒ Góc gi a m t ph ng (ữ ặ ẳ Q) và m t ph ng (ặ ẳ Q) c n tìm làầ
6 3
cos 1 9 3
α = − =
0.25
Gi s (ả ử Q) đi qua (∆) có d ng: ạm(2x + y + 1) + n(x + z − 2) = 0 (m2+ n2 > 0)
⇔ (2m + n)x + my + nz + m − 2n = 0
V y góc gi a (ậ ữ P) và (Q) là:
2 2
| 3 | 3
cos 3
3. 5 2 4
m
m n mn
α = =
+ +
0.25
⇔ m2 + 2mn + n2 = 0 ⇔ (m + n)2 = 0 ⇔ m = −n.
Ch n ọm = 1, n = −1, ta có: m t ph ng (ặ ẳ Q) là: x + y − z + 3 = 0 0.25
IV 1/. Ph ng trình ti p tuy n t i đi m có hoành đ ươ ế ế ạ ể ộ x = 2 là: y = 4x − 4 0.25
Th tích v t th tròn xoay c n tìm là:ể ậ ể ầ
2 2
4 2
0 1
(4 4)V x dx x dx
= π − −
÷
÷
∫ ∫
0.25
=
53
2 2
16 16
( 1)
0 1
5 3 15
xx
π
π − − =
÷
0.5
2/. Ta có:
[ ]
1 1 1
(1 ) (1 ) (1 ) 9
111
xy yz zx xy yz zx
+ + + + + + + ≥
÷
+++
0.25
2 2 2
9 9
33
Pxy yz zx x y z
⇔ ≥ ≥
+ + + + + +
0.25
⇒
9 3
6 2
P≥ =
0.25
V y GTNN là ậPmin =
3
2
khi x = y = z0.25
V
1/. Gi s đ ng th ng (ả ử ườ ẳ ∆) có d ng: ạAx + By + C = 0 (A2 + B2 > 0)
(∆) là ti p tuy n c a (ế ế ủ E) ⇔ 8A2 + 6B2 = C2 (1)
(∆) là ti p tuy n c a (ế ế ủ P) ⇔ 12B2 = 4AC ⇔ 3B2 = AC (2)
0.25
Th (2) vào (1) ta có: ếC = 4A ho c ặC = −2A.
V i ớC = −2A ⇒ A = B = 0 (lo i)ạ0.25
V i ớC = 4A ⇒
2
3
A
B= ±
⇒ Đ ng th ng đã cho có ph ng trình: ườ ẳ ươ
2 2 3
4 0 4 0
3
3
A
Ax y A x y± + = ⇔ ± + =
0.25
V y có hai ti p tuy n c n tìm: ậ ế ế ầ
2 3 4 0
3
x y± + =
0.25
V
Ta có:
12
12 12
4 4 12 4
12
0
1 1 1
1 1 ( 1)
k
k k
k
x x C x
x x x
−
=
+ − = − + = − +
÷ ÷ ÷
∑
0.25