S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ KỲ THI TUY N SINH VÀO L P 10 THPT NĂM H C 2012Ể Ớ Ọ
Đ NG NAIỒ Khóa ngày : 29 , 30 / 6 / 2012
Môn thi : TOÁN H CỌ
Th i gian làm bài : 120 phútờ
( Đ này có 1 trang , 5 câu )ề
Câu 1 : ( 1,5 đi m )ể
1 / Gi i ph ng trình : 7xả ươ 2 – 8x – 9 = 0 .
2 / Gi i h ph ng trình : ả ệ ươ
3x + 2y =1
4x +5y = 6
Câu 2 : ( 2,0 đi m )ể
1 / Rút g n các bi u th c : ọ ể ứ
12 +3 3 2 2
M ; N
3 2 1
−
−
= =
2 / Cho x1 ; x2 là hai nghi m c a ph ng trình : xệ ủ ươ 2 – x – 1 = 0 .
Tính :
1 2
1 1
+
x x
.
Câu 3 : ( 1,5 đi m ) Trong m t ph ng v i h tr c t a đ Oxy cho các hàm s : ể ặ ẳ ớ ệ ụ ọ ộ ố
y = 3x2 có đ th ( P ) ; y = 2x – 3 có đ th là ( d ) ; y = kx + n có đ th là ( dồ ị ồ ị ồ ị 1 ) v i k và n làớ
nh ng s th c .ữ ố ự
1 / V đ th ( P ) .ẽ ồ ị
2 / Tìm k và n bi t ( dế1 ) đi qua đi m T( 1 ; 2 ) và ( dể1 ) // ( d ) .
Câu 4 : ( 1,5 đi m ) M t th a đ t hình ch nh t có chu vi b ng 198 m , di n tích b ng 2430 mể ộ ử ấ ữ ậ ằ ệ ằ 2 .
Tính chi u dài và chi u r ng c a th a đ t hình ch nh t đã cho .ề ề ộ ủ ử ấ ữ ậ
Câu 5 : ( 3,5 đi m )ể
Cho hình vuông ABCD . L y đi m E thu c c nh BC , v i E không trùng B và E không trùngấ ể ộ ạ ớ
C . V EF vuông góc v i AE , v i F thu c CD . Đ ng th ng AF c t đ ng th ng BC t i G . Vẽ ớ ớ ộ ườ ẳ ắ ườ ẳ ạ ẽ
đ ng th ng a đi qua đi m A và vuông góc v i AE , đ ng th ng a c t đ ng th ng DE t i đi mườ ẳ ể ớ ườ ẳ ắ ườ ẳ ạ ể
H .
1 / Ch ng minh ứ
AE CD
AF DE
=
.
2 / Ch ng minh r ng t giác AEGH là t giác n i ti p đ c đ ng tròn .ứ ằ ứ ứ ộ ế ượ ườ
Đ CHÍNH TH CỀ Ứ
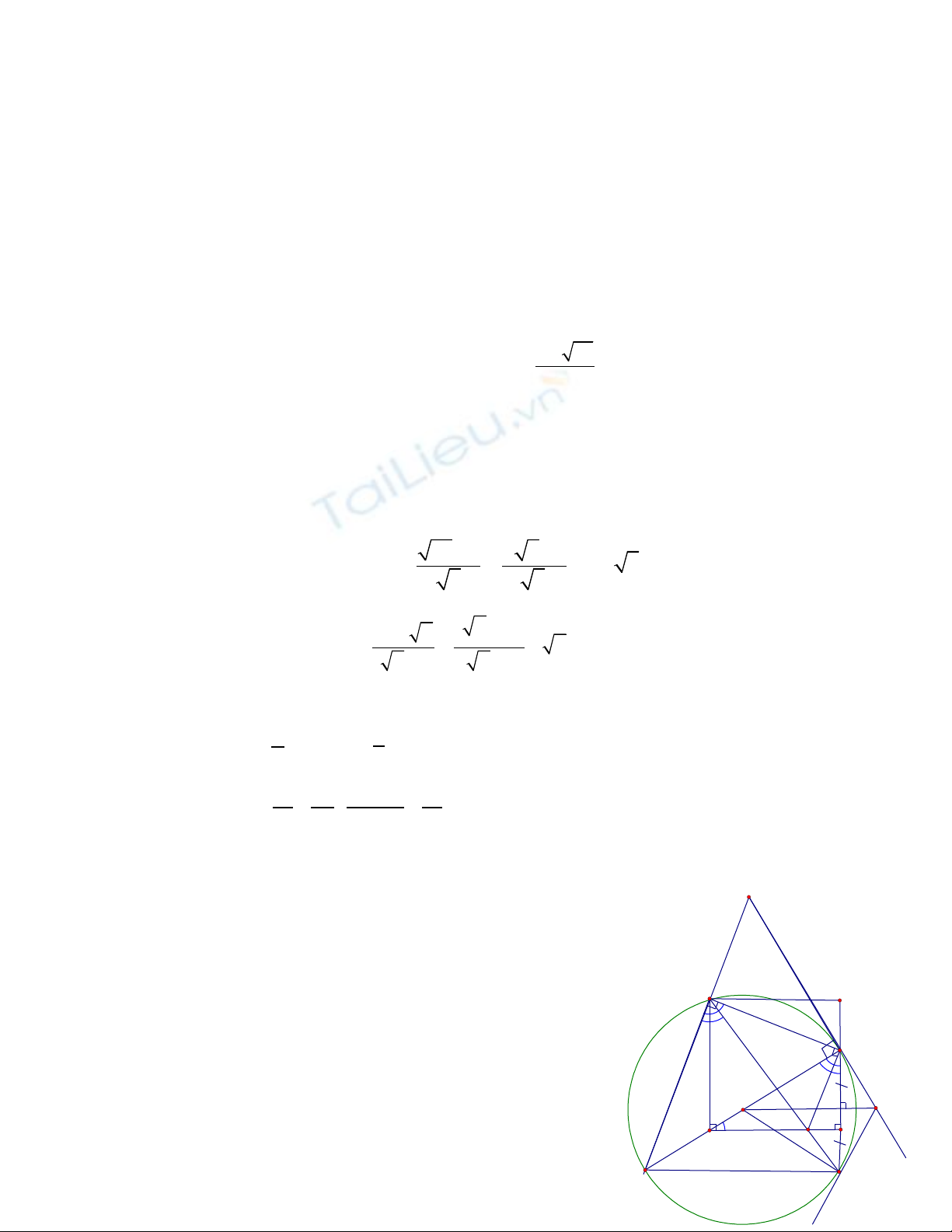
3 / G i b là ti p tuy n c a đ ng tròn ngo i ti p tam giác AHE t i E , bi t b c t đ ngọ ế ế ủ ườ ạ ế ạ ế ắ ườ
trung tr c c a đo n th ng EG t i đi m K . Ch ng minh r ng KG là ti p tuy n c a đ ng trònự ủ ạ ẳ ạ ể ứ ằ ế ế ủ ườ
ngo i ti p tam giác AHE .ạ ế
H NG D N GI I:ƯỚ Ẫ Ả
Câu 1 : ( 1,5 đi m )ể
1 / Gi i ph ng trình : 7xả ươ 2 – 8x – 9 = 0 ( x1,2 =
4 79
7
)
2 / Gi i h ph ng trình : ả ệ ươ
3x + 2y =1
4x + 5y = 6
( x ; y ) = (–1 ; 2 )
Câu 2 : ( 2,0 đi m )ể
1 / Rút g n các bi u th c : ọ ể ứ
12 +3 2 3 3
M 2 3
3 3
+
= = = +
( )
2
2 1
3 2 2
N 2 1
2 1 2 1
−
−= = −
− −
=
2 / Cho x1 ; x2 là hai nghi m c a ph ng trình : xệ ủ ươ 2 – x – 1 = 0 .
S =
; P =
Nên :
1 2
1 2 1 2
11
1
x x
1 1
+
x x x x
+
= = =−
−
Câu 3 : ( 1,5 đi m )ể
1 / V đ th ( P ) .ẽ ồ ị
2 / ( d1 ) // ( d ) nên k = 2 ; n
–3 và đi qua đi m T( 1 ; 2 ) nên x = 1 ; y = 2 . Ta có ph ngể ươ
trình : 2 = 1.2 + n
n = 0
Câu 4 : ( 1,5 đi m )ể
G i x ( m ) là chi u dài th a đ t hình ch nh t ( 49,5 < x < 99 )ọ ề ử ấ ữ ậ
Chi u r ng c a th a đ t hình ch nh t là : 99 – x ( m )ề ộ ủ ử ấ ữ ậ
1
2
1
1
K
I
b
a
G
H
F
E
D
C
B
A
Theo đ bài ta có ph ng trình : x ( x – 99 ) = 2430ề ươ
Gi i đ c : xả ượ 1 = 54 ( nh n ) ; xậ2 = 45 ( lo i )ạ
V y chi u dài th a đ t hình ch nh t là 54 ( m ) ậ ề ử ấ ữ ậ
Chi u r ng c a th a đ t hình ch nh t là : 99 – 54 = 45 ( m )ề ộ ủ ử ấ ữ ậ
Câu 5 : ( 3,5 đi m )ể
1 / Ch ng minh t giác AEFD n i ti pứ ứ ộ ế
ﾶ
ﾶ
1 1
A D=�
∆
AEF
∆
DCE ( g – g )
AE AF
=
DC DE
AE DC
=
AF DE
2 / Ta có
ﾶ
2
A
ph v iụ ớ
ﾶ
1
A
Ta có
ﾶ
1
E
ph v i ụ ớ
ﾶ
1
D
Mà
ﾶ
ﾶ
1 1
A D=
ﾶ
ﾶ
2
1
A E=�
Suy ra t giác AEFD n i ti p đ ng tròn đ ng kính HEứ ộ ế ườ ườ
G i I trung đi m c a HEọ ể ủ
I là tâm đ ng tròn ngo i ti p t giác AEFD cũng là đ ngườ ạ ế ứ ườ
tròn ngo i ti p ạ ế
ΔAHE
I n m trên đ ng trung tr c EG ằ ườ ự
IE = IG
Vì K n m trên đ ng trung tr c EG ằ ườ ự
KE = KG
Suy ra
∆
IEK =
∆
IGK ( c-c-c )
ﾶ
ﾶ
0
IGK IEK 90
=
=�
KG IG
⊥�
t i G c a đ ng tròn ngo i ti p ạ ủ ườ ạ ế
ΔAHE
KG là ti p tuy n c a đ ng tròn ngo i ti pế ế ủ ườ ạ ế
ΔAHE