1
1
ðINTS
Trnh Văn Loan
Khoa CNTT ðHBK
http://cnpmk51bkhn.org 2
Tàiliuthamkh o
Bài ging này (quan trng !)
K thut s
Lý thuy"t m#ch lôgic &k thut s
K thut ñi(n t) s
…
http://ktmt.shorturl.com
http://cnpmk51bkhn.org
3
Chương1.
Cáchàmlôgiccơb n
http://cnpmk51bkhn.org 4
1.1ð*is,Boole
Cácñnhnghĩa
•Bi0nlôgic:ñ#ilư/ngbi0udi2n
b3ngkýhi(unàoñó,l6ygiátr80
ho:c1
•Hàmlôgic:nhómcácbi"nlôgic
liênh(v=inhauquacácphép
toánlôgic,l6ygiátr80ho:c1
•Phéptoánlôgiccơb n:
VÀ(AND),HOIC(OR),PHMðONH
(NOT) http://cnpmk51bkhn.org
2
5
1.1ð*is,Boole
Bi5udi7nbi0nvàhàmlôgic
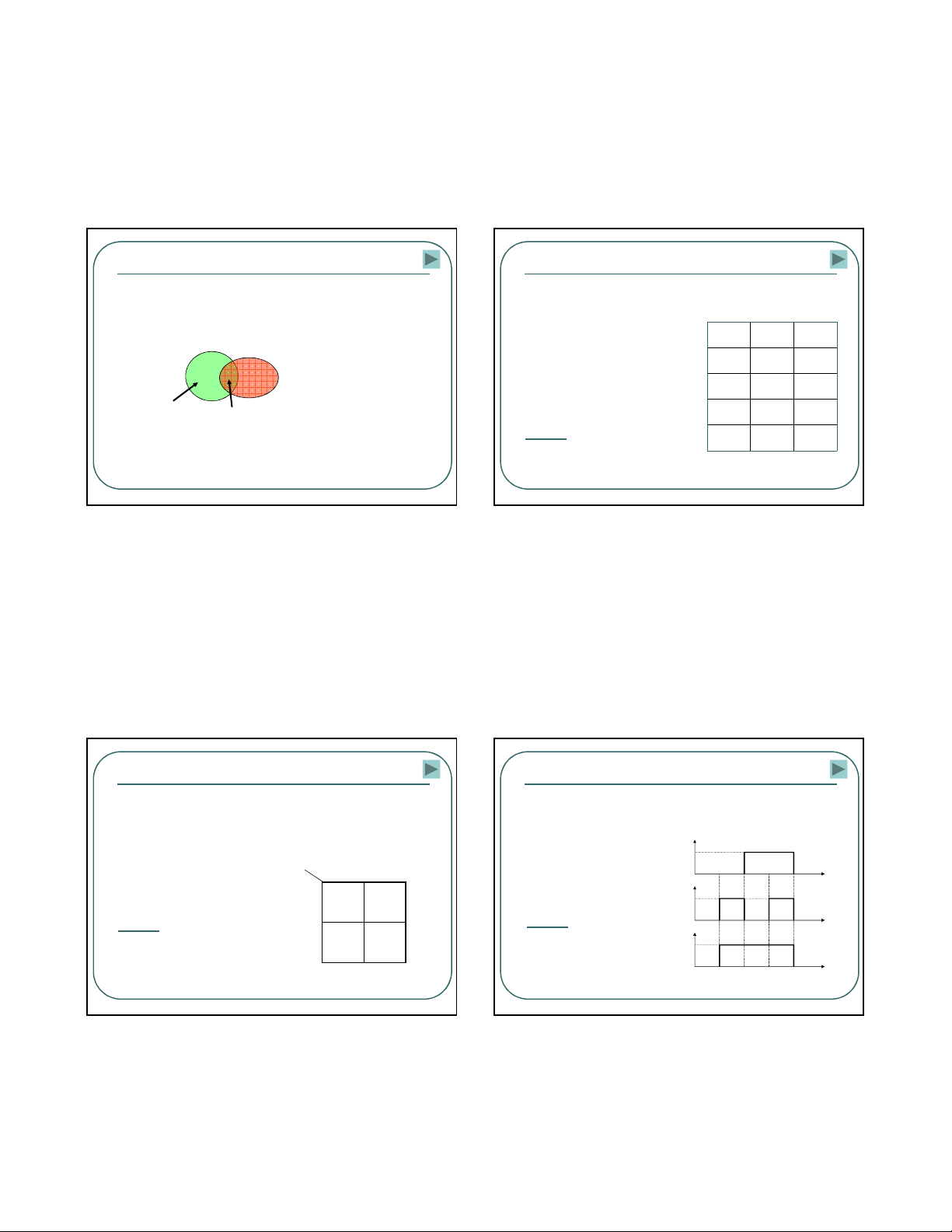
•Bi5uñ9Ven:
Aho;cB AvàB
MRibi"nlôgicchia
khônggianthành2
khônggiancon:
1khônggiancon:
bi"nl6ygiátr8ñúng
(=1)
Khônggiancon
cònl#i:bi"nl6ygiá
tr8sai(=0)
AB
http://cnpmk51bkhn.org 6
1.1ð*is,Boole
Bi5udi7nbi0nvàhàmlôgic
•B ngth<t:
Hàmnbi"nsWcó:
n+1cYt(nbi"nvà
giátr8hàm)
2nhàng:2ntZh/p
bi"n
Víd> Bngththàm
Ho:c2bi"n
A B F(A,B)
0 0 0
0 1 1
1 0 1
1 1 1
http://cnpmk51bkhn.org
7
1.1ð*is,Boole
Bi5udi7nbi0nvàhàmlôgic
•BìaCacnô:
SôtrênbìaCacnô
b3ngsdòngbng
tht
Víd> BìaCacnôhàm
Ho:c2bi"n
0 1
1 1
AB0 1
0
1
http://cnpmk51bkhn.org 8
1.1ð*is,Boole
Bi5udi7nbi0nvàhàmlôgic
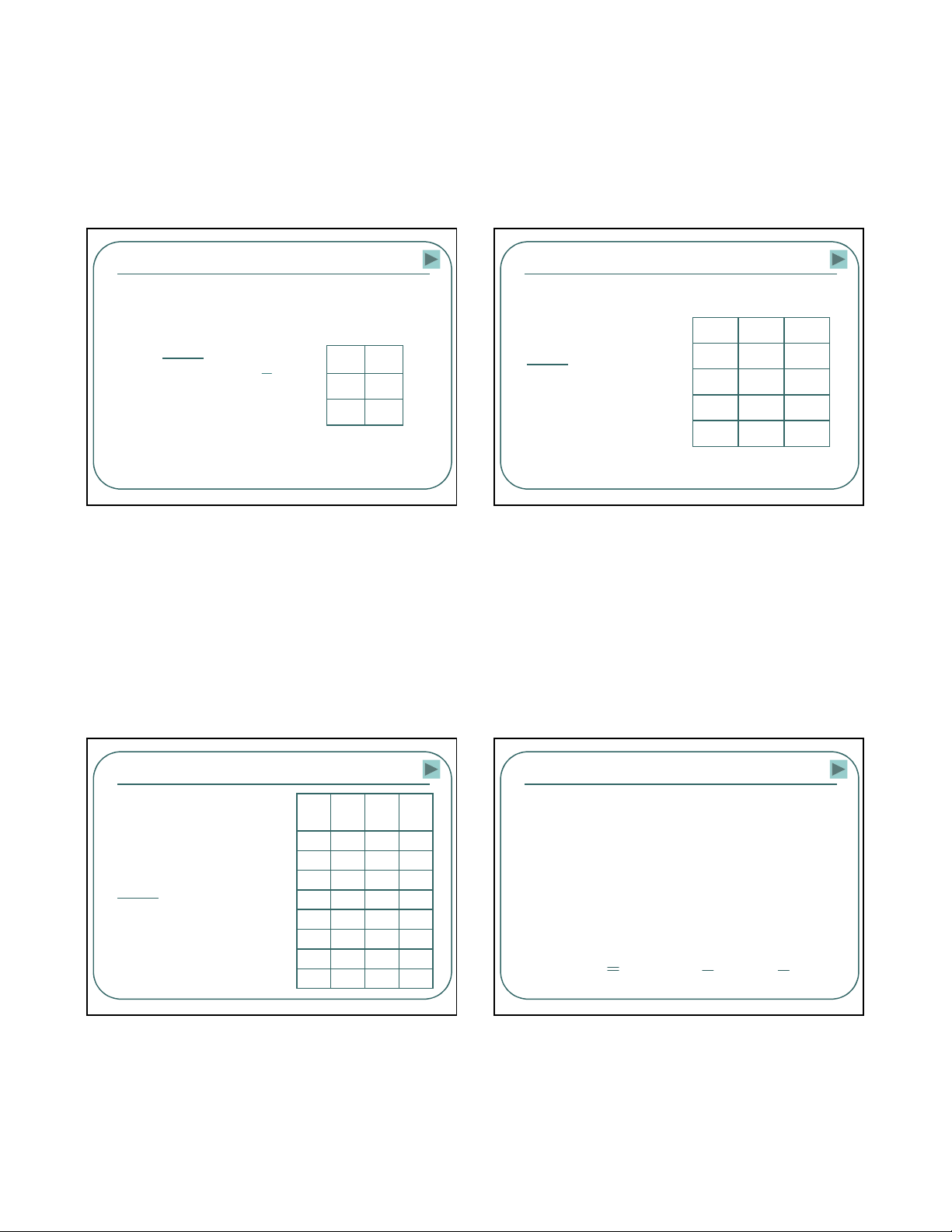
•Bi5uñ9th@igian:
Làñ`th8bi"nthiên
theothbigiancca
hàmvàbi"nlôgic
Víd> Bi0uñ`
thbigiancca
hàmHo:c2bi"n
t
t
t
A
1
0
F(A,B)
0
B
1
0
1
http://cnpmk51bkhn.org
3
9
1.1ð*is,Boole
Cáchàmlôgiccơb n
•HàmPhFñnh:
Víd> Hàm1bi"n
=
F(A) A
A F(A)
0 1
1 0
http://cnpmk51bkhn.org 10
1.1ð*is,Boole
Cáchàmlôgiccơb n
•HàmVà:
Víd> Hàm2bi"n
A B F(A,B)
000
010
100
111
=
F(A,B) AB
http://cnpmk51bkhn.org
11
Cáchàmlôgiccơb n
•HàmHo;c:
Víd> Hàm3bi"n
A B C F
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
1.1ð*is,Boole
= + +
F(A,B,C) A B C
http://cnpmk51bkhn.org 12
TínhchGtcáchàmlôgiccơb n
T`nt#iphent)trungtínhduynh6tchophéptoán
Ho:cvàphéptoánVà:
A+0=A A.1=A
Giaohoán: A+B=B+A A.B=B.A
K"th/p:A+(B+C)=(A+B)+C=A+B+C
A.(B.C)=(A.B).C=A.B.C
Phânphi: A(B+C)=AB+AC
A+(BC)=(A+B)(A+C)
Khôngcósmũ,khôngcóh(s:
Phépbù:
= + = =
A AA A 1A.A 0
1.1ð*is,Boole
+ + + =
=
A.A....A A
http://cnpmk51bkhn.org
4
13
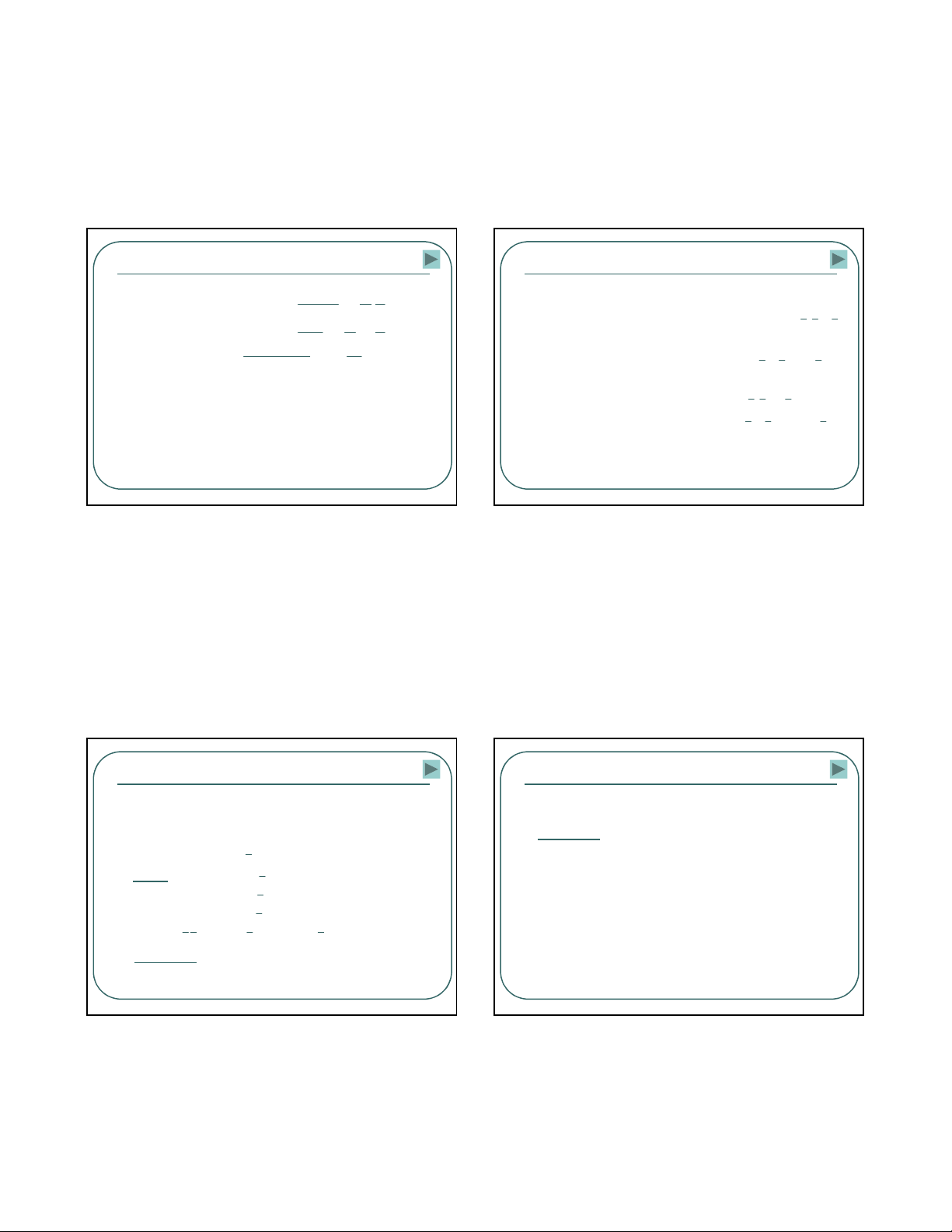
ðnhlýð@Moocgan
+ =
= +
A B A.B
A.B A B
+ = +
i i
F(X , ,.) F(X ,., )
Trưbngh/p2bi"n
TZngquát
TínhchGtñ,ingJu
•
+ ⇔ ⇔
0 1
+ = + ⇔ =
+ = ⇔ =
A B B A A.B B.A
A 1 1 A.0 0
1.1ð*is,Boole
http://cnpmk51bkhn.org 14
1.2Bi5udi7ncáchàmlôgic
D*ngtuy5nvàd*nghNi
D*ngchínhqui
= + +
F(x,y,z) xyz xy xz
= + + + + +
F(x,y,z) (x y z)(x y)(x y z)
•Tuy0nchínhqui
•HYichínhqui
= + +
F(x,y,z) xyz xyz xyz
= + + + + + +
F(x, y,z) (x y z)(x y z)(x y z)
Khôngphid#ngchínhquitnclàd#ngñơnginhóa
•D#ngtuy0n(tZngcáctích)
•D#nghYi(tíchcáctZng)
http://cnpmk51bkhn.org
15
1.2Bi5udi7ncáchàmlôgic
D*ngtuy5nchínhqui
ð8nhlýShannon:T6tccáchàmlôgiccóth0tri0n
khaitheomYttrongcácbi"ndư=id#ngtZngcca2
tíchlôgic:
= +
F(A,B,...,Z) A.F(0,B,...,Z) A.F(1,B,...,Z)
Víd>
= +
F(A,B) A.F(0,B) A.F(1,B)
= +
F(0,B) B.F(0,0) B.F(0,1)
= +
F(1,B) B.F(1,0) B.F(1,1)
= + + +
F(A,B) AB.F(0,0) AB.F(0,1) AB.F(1,0) AB.F(1,
1)
Nh<nxét
2bi"n→TZng4sh#ng,3bi"n→TZng8sh#ng
nbi"n→TZng2nsh#ng
http://cnpmk51bkhn.org 16
1.2Bi5udi7ncáchàmlôgic
D*ngtuy5nchínhqui
Nh<nxét
Giátr8hàm=0→
sh#ngtươngnngb8lo#i
Giátr8hàm=1→
sh#ngtươngnngb3ngtíchcácbi"n
http://cnpmk51bkhn.org
5
17
1.2Bi5udi7ncáchàmlôgic
D*ngtuy5nchínhqui
A B C F
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 0
1 1 1 1
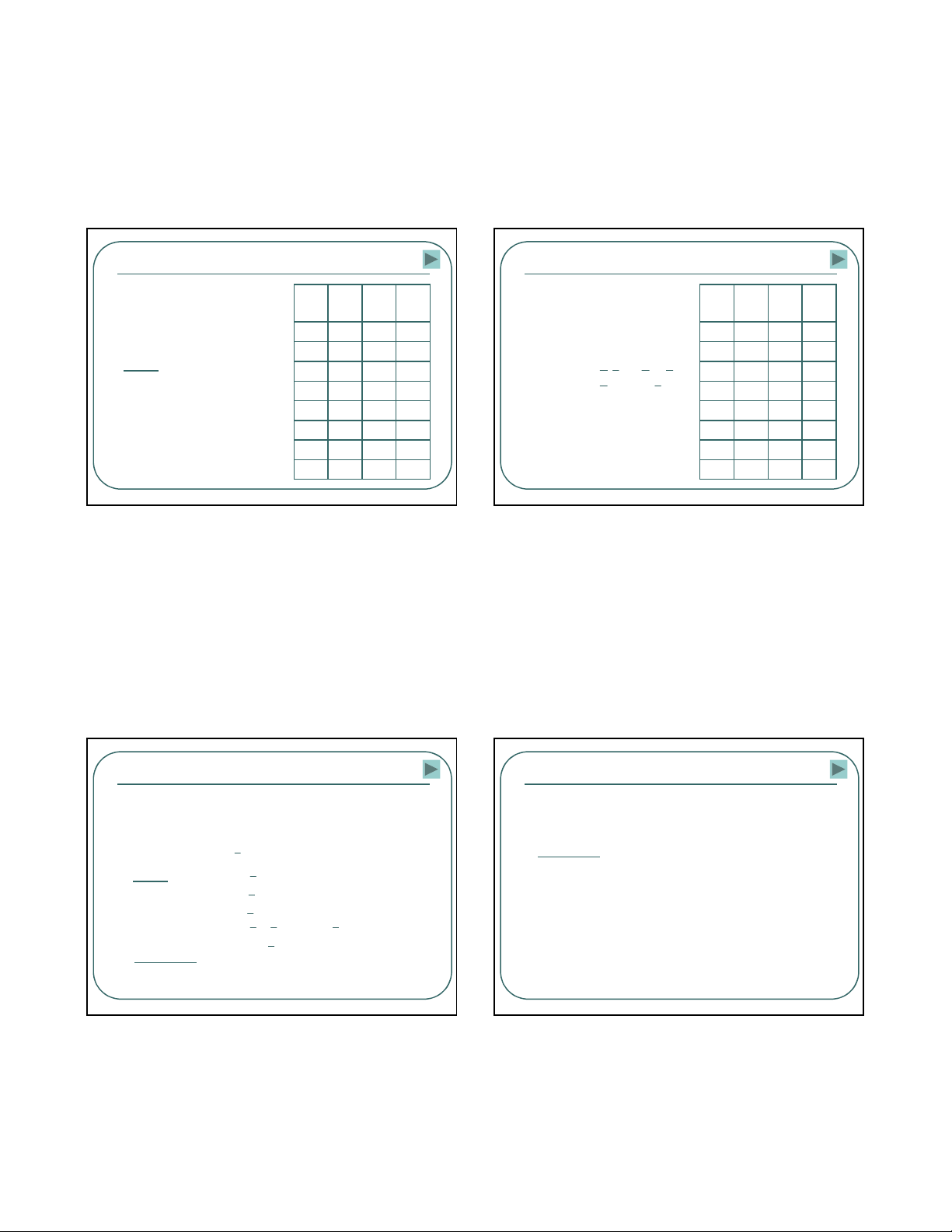
Víd>
Chohàm3bi"nF(A,B,C).
Hãyvi"tbi0uthnchàm
dư=id#ngtuy0nchínhqui.
http://cnpmk51bkhn.org 18
1.2Bi5udi7ncáchàmlôgic
=++
+ +
F(A,B,C) ABC ABC
ABC ABC
ABC
D*ngtuy5n
chínhqui A B C F
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 0
1 1 1 1
http://cnpmk51bkhn.org
19
D*nghNichínhqui
ð8nhlýShannon:T6tccáchàmlôgiccóth0tri0n
khaitheomYttrongcácbi"ndư=id#ngtíchcca2
tZnglôgic:
= + +F(A,B,...,Z) [A F(1,B,...,Z)].[A F(0,B,...,
Z)]
= + +
F(A,B) [A F(1,B)][A F(0,B)]
= + +
F(0,B) [B F(0,1)][B F(0,0)]
= + +
F(1,B) [B F(1,1)][B F(1,0)]
= + + + +
+ + + +
F(A,B) [A B F(1,1)][A B F(1,0)]
[A B F(0,1)][A B F(0,0)]
1.2Bi5udi7ncáchàmlôgic
2bi"n→Tích4sh#ng,3bi"n→Tích8sh#ng
nbi"n→Tích2nsh#ng
Nh<nxét
Víd>
http://cnpmk51bkhn.org 20
D*nghNichínhqui
Nh<nxét
Giátr8hàm=1→
sh#ngtươngnngb8lo#i
Giátr8hàm=0→
sh#ngtươngnngb3ngtZng cácbi"n
1.2Bi5udi7ncáchàmlôgic
http://cnpmk51bkhn.org