Tiết1- 2 : ĐỊNH NGHĨA VÀ Ý NGHĨA CỦA ĐẠO HÀM
I. MỤC ĐÍCH: Qua tiết dạy này nhằm giúp cho học sinh nắm:
Kiến Thức:
- Hiểu rõ định nghĩa đạo hàm của hàm số tại một điểm ,lưu ý đạo hàm của hàm số tại
một điểm là một số xác định
- Nắm vững ý nghĩa hình học của đạo hàm(hai chú ý:hệ số góc của tiếp tuyến
và phương trình tiếp tuyến)
- Tính được đạo hàm bằng định nghĩa dựa vào công thức f/ (x0) =
x
y
x
0
lim và bước đầu vận
dụng được ý nghĩa đạo hàm để viết phương trình tiếp tuyến
Kỹ năng:
- Rèn luyện kĩ năng tính đạo hàm tại một điểm
- Rèn luyện cho học sinh kĩ năng viết phương trình tiếp tuyến của hàm số tại
điểm M(x0,y0) với đồ thị (C ) của hàm số y = f(x)
Tư duy:
- Rèn luyện cho học sinh tư duy lô gic
- Cho học sinh bước đầu thấy được tác dụng của đạo hàm vào thực tế
Thái độ:
- Cẩn thận trong lời giải ,chính xác trong tính toán và lập luận ngắn gọn
- Thái độ vui vẽ trong việc học nhóm,tích cực xây dựng bài
II. PHƯƠNG PHÁP:
- Gợi mở vấn đáp
- Chia nhóm nhỏ học tập
- Phân bậc hoạt động các nội dung học tập theo bảng
III. PHƯƠNG TIỆN DẠY HỌC:
- Chuẩn bị các hình vẽ
- Chuẩn bị máy chiếu
- Phần mềm sketchpad
IV. TIẾN TRÌNH BÀY DẠY:
Tình huống 1:
Kiểm tra lại các kiến thức của học sinh thông qua HĐ cho học sinh trả lời câu hỏi
+ Hoạt động 1: Tìm hiểu nhiệm vụ của học sinh
+ Hoạt động 2: Học sinh tìm hiểu nhiệm vụ của mình thông qua các câu hỏi của giáo
viên
Tình huống 2:
Cho học sinh tiếp cận nội dung kiến thức mới thông qua các ví dụ trong thực tế bằng cách
tham khảo và tìm hiểu các tình huống trong sách giáo khoa
+ Hoạt động 1: Tìm hiểu khả năng lĩnh hội câu hỏi, cũng như nhiệm vụ của học sinh
+ Hoạt động 2: Học sinh lĩnh hội câu hỏi và có thể tự giải quyết công việc thông qua
sự dẫn dắt của giáo viên
- Giáo viên: Trình chiếu nội dung câu hỏi lên máy
- Học sinh: Trả lời câu hỏi theo yêu cầu của giáo viên
Hoạt động giáo viên và học sinh Ghi bảng
1. Bài mới:
HĐ1 Giới thiệu nêu nội dung bài toán và
dùng hình vẽ minh họa sự chuyển động của
viên bi
Lưu ý :
-Vận tốc trung bình
-Vận tốc tức thời
0
0)()(
lim
0xx
xfxf
xx
thường gặp trong các bài
toán vật lí ; hoá học; …
1. Ví dụ mở đầu : (sgk)
Lưu ý :
1 0
1 0
( ) ( )
f t f t
t t
là vận tốc trung bìnhcủa
chuyển động
1 0
1 0
0
1 0
( ) ( )
lim
t t
f t f t
v t t t
là vận tốc tức thời
của chuyển động tại t0
0
0)()(
lim
0xx
xfxf
xx
=
x
y
Trong đó f(x) là hàm số của đối số x
2.Đạo hàm của hàm số tại một điểm
a. Khái niệm đạo hàm của hàm số tại
một điểm
HĐ2 Giới thiệu định nghìa đạo hàm
- Gv giới thiệu khái niệm đạo hàm của hàm
số tại một điểm
- Gv giới thiệu cách tính đạo hàm bằng định
nghìa
- Hs vận dụng cách tính đạo hàm bằng định
0
/
0
0
( ) ( )
lim
x x
f x f x
f x x x
gọi là đạo hàm của hàm số y = f(x) tại x0
Lưu ý : (sgk)
x = x - x0 số gia của đối số
y = f(x) - f(x0) số gia của hàm số
x
xfxxf
xf x
)()(
lim)( 00
0
0
/
b.Cách tính đạo hàm bằng định nghĩa
Tính y = f(x0 + x) – f(x0)
Tính
y
xf x0
0
/lim)(
Ví dụ : Tính đạo hàm của hàm số
y = x2 tại điểm x0 = 2
/00
( ) lim
x
y
f x
x
=
0
lim 4
x
x
= 4
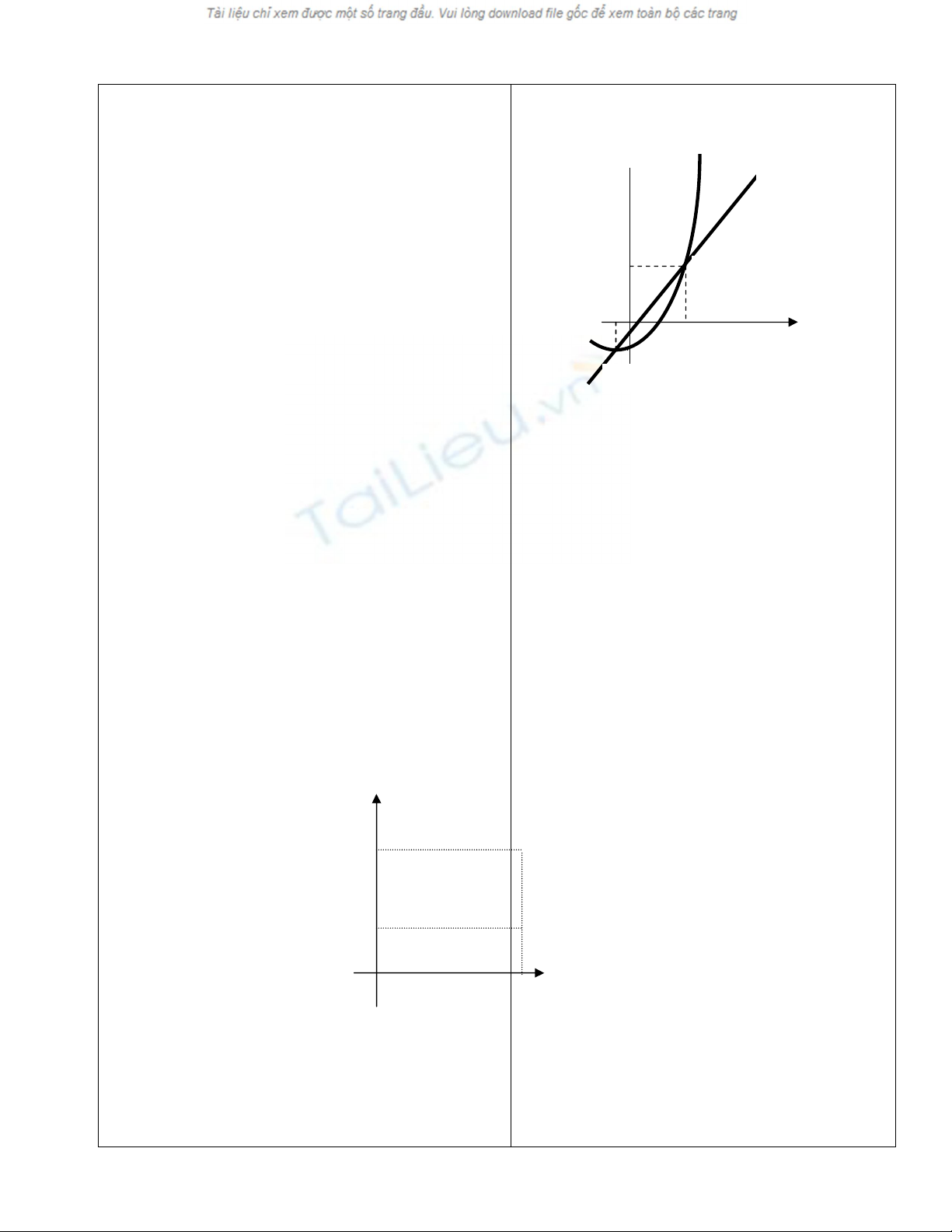
3.Ý nghĩa hình học của đạo hàm
a.Tiếp tuyến của đường cong phẳng
nghìa d
ể giải các ví dụ
HĐ3 Giới thiệu ý nghĩa hình học của đạo
hàm
- Gv dùng hìmh vẽ giới thiệu cát tuyến và
tiếp tuyến của đường cong phẳng
Lưu ý :
- Hệ số góc của tiếp tuyến f '(x
0
)
f '(x0) là hệ số góc của tiếp tuyến của đồ
thị hàm số y = f(x) tại điểm M(x0,f(x0))
y = f '(x0)(x - x0 ) + y0
là phương trình tiếp tuyến của đồ thị hàm
số y = f(x) tại điểm M(x0,f(x0))
Ví dụ : Viết phương trình tiếp tuyến của
parabol: y = -x² + 3x -2 tại điểm có hoành
độ x0 = 2
4.Ý nghĩa cơ học của đạo hàm
M0
M
(C )