3./Đ ng H c Thu n: ộ ọ ậ
Qui T c Denavit-Hartenbergắ
B c 1: ướ Xác đ nh các tr c kh p và đ t tên t ng ngị ụ ớ ặ ươ ứ
10 −n
zz
.
B c 2: ướ Xác l p h t a đ n n. Đ t g c c a h t a đ này t i b t kỳ đi m nào trênậ ệ ọ ộ ề ặ ố ủ ệ ọ ộ ạ ấ ể
tr c ụ
0
z
. Các tr c ụ
0
x
và
0
y
đ c ch n th a qui t c tam di n thu n. ượ ọ ỏ ắ ệ ậ
L p ặ
1,...,1 −= ni
l n th c hi n b c 3 đ n b c 5.ầ ự ệ ướ ế ướ
B c 3:ướ Xác đ nh các g c ị ố
i
O
là giao đi m c a đ ng vuông góc chung gi aể ủ ườ ữ
i
z
và
1−i
z
v i ớ
. N u ế
i
z
giao v i ớ
1−i
z
, đ t ặ
i
O
t i giao đi m này. N uạ ể ế
song song v i ớ
1−i
z
, đ tặ
i
O
t i b t kỳ v trí nào trên ạ ấ ị
sao cho thu n ti n.ậ ệ
B c 4:ướ Xác đ nh ị
d c theo đ ng vuông góc chung gi a ọ ườ ữ
1−i
z
và
i
z
đi qua
i
O
, ho cặ
theo h ng vuông góc v i m t ph ng t o b i ướ ớ ặ ẳ ạ ở
1−i
z
và
n u ế
1−i
z
và
giao nhau.
B c 5:ướ Xác đ nh ị
i
y
th a qui t c tam di n thu n.ỏ ắ ệ ậ
B c 6ướ : Xác đ nh h t a đ tác đ ng cu i ị ệ ọ ộ ộ ố
nnnn zyxo
. Gi s kh p ả ử ớ
n
là kh p quay,ớ
đ t ặ
azn=
d c theo h ng ọ ướ
1−n
z
. Xác đ nh g c ị ố
n
O
b t kỳ trên ấ
n
z
sao cho thu n ti n,ậ ệ
th ng là tâm c a b k p hay t i đ u d ng c mà tay máy ph i mang. Đ t ườ ủ ộ ẹ ạ ầ ụ ụ ả ặ
syn=
theo h ng k p và đ t ướ ẹ ặ
n
x
theo
as x
. N u d ng c k p không đ n gi n thì đ t ế ụ ụ ẹ ơ ả ặ
n
x
và
n
y
t o thành tam di n thu n.ạ ệ ậ
B c 7ướ : L p b ng tham s ch các khâu trên robotậ ả ố
i
a
: kho ng cách theo ph ng ả ươ
i
x
t ừ
i
O
đ n giao đi m c a các tr c ế ể ủ ụ
i
x
và
1−i
z
.
i
d
: kho ng cách theo ph ng ả ươ
1−i
z
t ừ
1−i
O
đ n giao đi m c a các tr c ế ể ủ ụ
i
x
và
1−i
z
,
i
d
thay đ i khi kh p ổ ớ
i
là kh p tr t.ớ ượ
i
α
: là góc quay quanh tr c ụ
i
x
t ừ
1−i
z
đ n ế
.
i
θ
: là góc quay quanh tr cụ
1−i
z
t ừ
1−i
x
đ n ế
i
x
.
B c 8ướ : T các ma tr n bi n đ i thu n nh t ừ ậ ế ổ ầ ấ
i
A
b ng cách thay các tham s trên vào.ằ ố
B c 9ướ : Tính
nn AAT
1
0=
. Ma tr n này cho ta bi t đ c v trí và h ng đ i v i hậ ế ượ ị ướ ố ớ ệ
t a đ n n c a d ng c g n trên khâu cu i. ọ ộ ề ủ ụ ụ ắ ố
Ví d 3.1:ụ
1
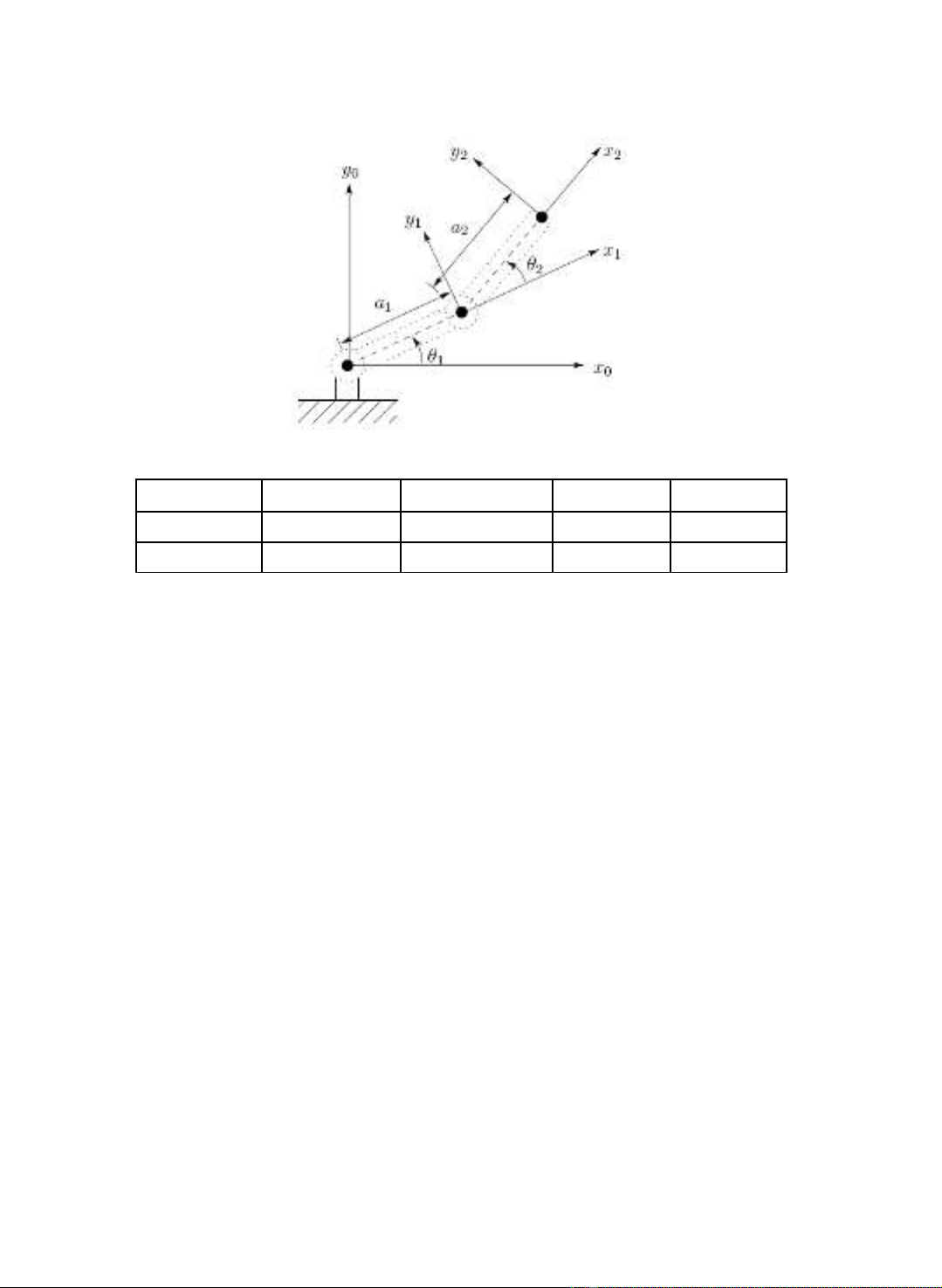
Hình 3.1: Tay máy hai khâu ph ng.ẳ
B ng tham s khâu cho robot 2 khâu đ ng ph ngả ố ồ ẳ
Khâu
i
a
i
α
i
d
i
θ
1
1
a
0 0
1
θ
2
2
a
0 0
2
θ
−
=
−
=
1000
0100
0
0
1000
0100
0
0
2222
2222
2
1111
1111
1
sacs
casc
A
sacs
casc
A
Ma tr n bi n đ i thu n nh tậ ế ổ ầ ấ
+
+−
==
1000
0100
0
0
122111212
122111212
21
0
2
sasacs
cacasc
AAT
L u ý r ng 2 thành ph n đ u c a c t cu i cùng c a ư ằ ầ ầ ủ ộ ố ủ
0
2
T
là v trí x và y c a ị ủ
2
O
.
12211
12211
sasay
cacax
+=
+=
2
Ph n quay c a ầ ủ
0
2
T
cho h ng c a ướ ủ
2222 zyxo
đ i v i h t a đ n n.ố ớ ệ ọ ộ ề
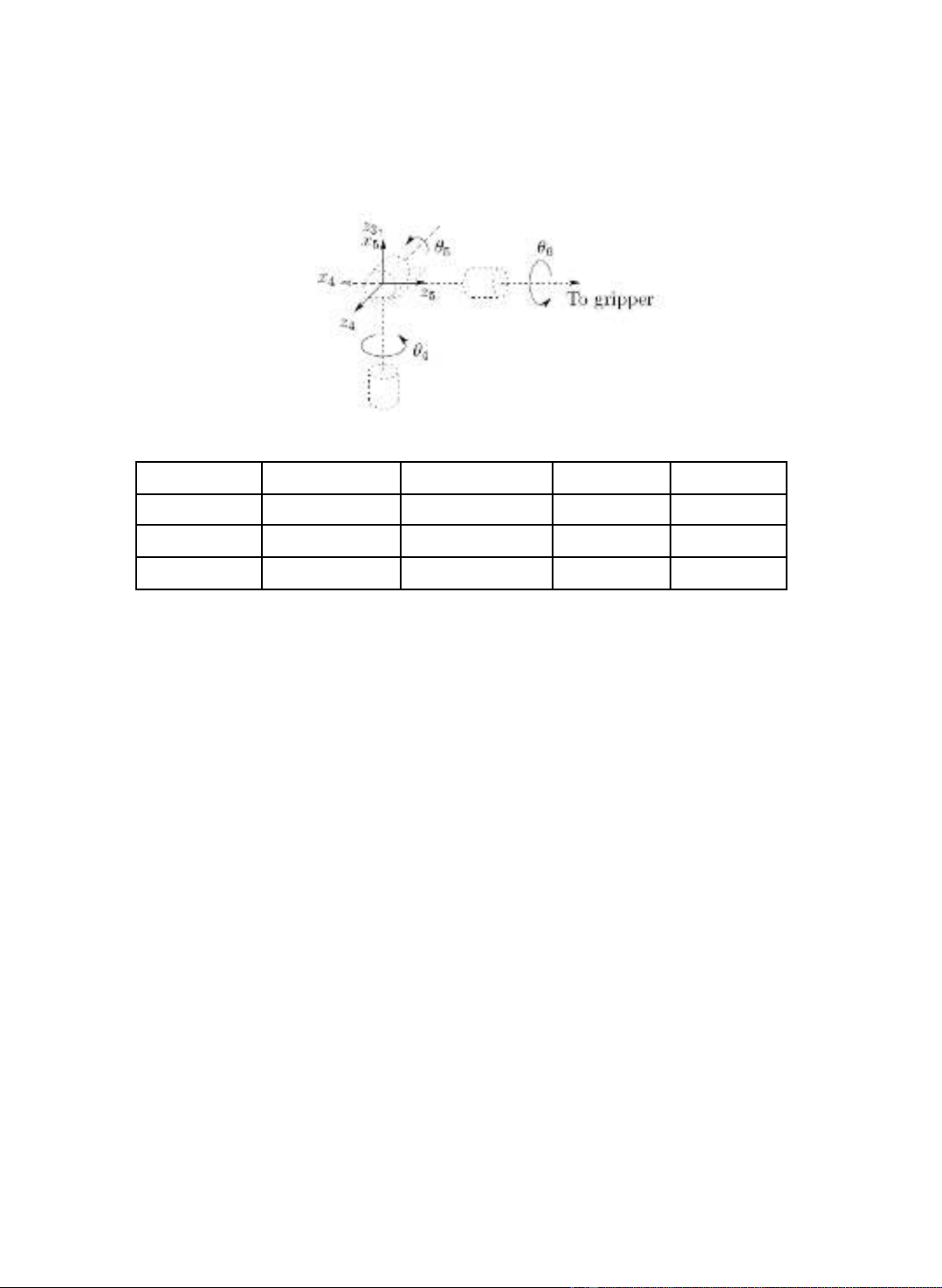
Ví d 3.2:ụ C tay kh p c u (Spherical Wrist)ổ ớ ầ
Tr c ụ
543 ,, zzz
đ ng quy t i đi m ồ ạ ể
. Tay máy Stanford có c tay thu c d ng này.ổ ộ ạ
Hình 3.2: Gán h tr c t a đ cho c tay kh p c uệ ụ ọ ộ ổ ớ ầ .
B ng 3.2ả: Tham s DH cho c tay kh p c u.ố ổ ớ ầ
Khâu
i
a
i
α
i
d
i
θ
4 0 -90 0
4
θ
5 0 90 0
5
θ
6 0 0
6
d
6
θ
Ta th y r ng ba bi n kh p cu i ấ ằ ế ớ ố
654
,,
θθθ
là các góc Euler
ψθφ
,,
t ng ng đ i v i hươ ứ ố ớ ệ
t a đ ọ ộ
3333 zyxO
. Ta có
−
−
=
1000
0010
00
00
44
44
4
cs
sc
A
;
−
−
=
1000
0010
00
00
55
55
5
cs
sc
A
;
−
=
1000
100
00
00
6
66
66
6d
cs
sc
A
−
+−+
−−
=
==
1000
10 6556565
654546465464654
6545465464654
3
6
3
6
654
3
6dccsscs
dssssccscsscccs
dscscsccssccc
OR
AAAT
So sánh ph n ma tr n quay ầ ậ
3
6
R
c a ủ
3
6
T
v i phép bi n đ i góc Euler. Đi u đó cho th yớ ế ổ ề ấ
r ng vai tròằ
654
,,
θθθ
hoàn toàn gi ng v i các góc Euler ố ớ
ψθφ
,,
đ i v i h t a đố ớ ệ ọ ộ
3333 zyxO
.
NL: Các góc Euler
Xét h t a đ c đ nh ệ ọ ộ ố ị
0000 zyxO
và h t a đ quay ệ ọ ộ
1111 zyxO
nh n đ c b i vi c th cậ ượ ở ệ ự
hi n 3 phép quay sau:ệ
3
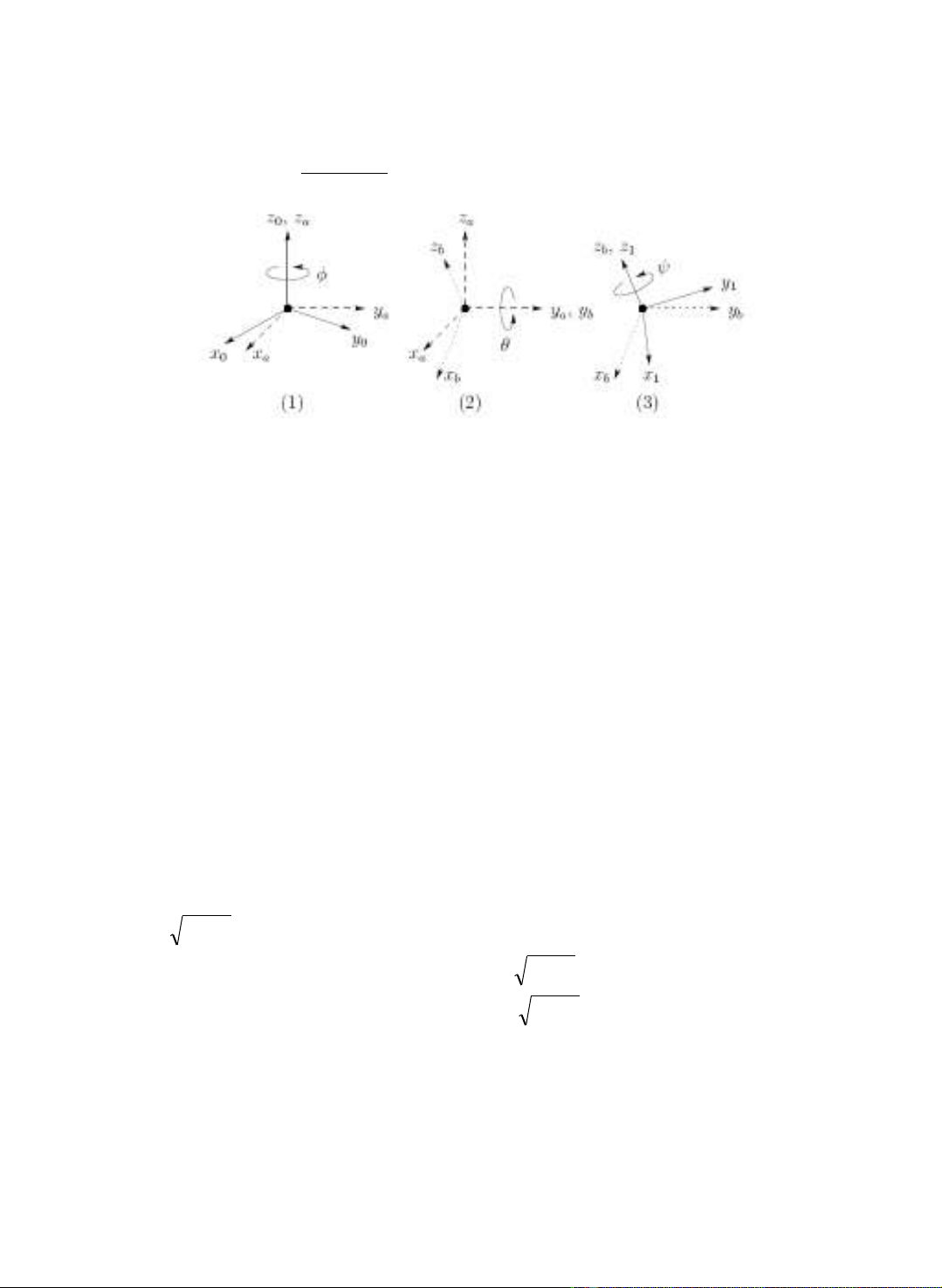
(1) Quay quanh tr c ụ
z
m t góc ộ
φ
;
(2) Quay quanh tr c ụ
y
hi n hànhệ m t góc ộ
θ
;
(3) Quay quanh tr c ụ
z
hi n hành m t góc ệ ộ
Hình 3.3: S bi u di n các góc Eulerự ể ễ
Ma tr n bi n đ i ậ ế ổ
−
+−+
−−−
=
−
−
−
=
=
θψθψθ
θφψφψθφψφψθφ
θφψφψθφψφψθφ
ψψ
ψψ
θθ
θθ
φφ
φφ
ψθφ
csscs
ssccscsscccs
sccssccssccc
cs
sc
cs
sc
cs
sc
RRRR zyz
100
0
0
0
010
0
100
0
0
,,,
0
1
Bây gi xét bài toán xác đ nh các góc ờ ị
ψθφ
,,
khi cho tr c ma tr n quayướ ậ
=
333231
232221
131211
rrr
rrr
rrr
R
Gi s r ng c hai ph n t ả ử ằ ả ầ ử
2313 ,rr
đ u không b ng 0. Có nghĩa là ề ằ
0
≠
θ
s
và vì th cế ả
3231,rr
đ u không b ng 0. N u c ề ằ ế ả
2313 ,rr
đ u không b ng 0 thì ề ằ
1
33 ±≠r
và ta có
33
rc =
θ
,
2
33
1rs −±=
θ
, nh v y ta cóư ậ
()
2
3333 1,tan rrA −=
θ
(3.1)
hay
()
2
3333 1,tan rrA −−=
θ
(3.2)
Tùy vào d u c a các tham s mà hàm Atan s ch n góc ph n t cho góc ấ ủ ố ẽ ọ ầ ư
θ
. N u cế ả
hai tham s b ng 0, thì hàm Atan không xác đ nh.ố ằ ị
N u ế
0
2313 == rr
, thì
1
33 ±=r
và
0
3231 == rr
. Vì v y ậ
R
có d ngạ
4
±
=
100
0
0
2221
1211
rr
rr
R
N u ế
1
33 =r
thì
1
=
θ
c
và
0
=
θ
s
, k t qu là ế ả
0
=
θ
. Trong tr ng h p này ườ ợ
0
1
R
tr thànhở
=
++
+−+
=
+−+
−−−
=
333231
232221
131211
0
1
100
0)()(
0)()(
100
0
0
rrr
rrr
rrr
cs
sc
ccsssccs
csscsscc
R
ψφψφ
ψφψφ
ψφψφψφψφ
ψφψφψφψφ
),tan(),tan( 12112111 rrArrA −==+⇒
ψφ
Có vô s nghi m trong tr ng h p này. Ta có th l y ố ệ ườ ợ ể ấ
0=
φ
, và xác đ nh ị
ψ
.
N u ế
1
33 −=r
, thì
1
−=
θ
c
và
0
=
θ
s
, k t qu là ế ả
πθ
=
. Ta có
=
−−
−−−−
=
333231
232221
131211
0
1
100
0)()(
0)()(
rrr
rrr
rrr
cs
sc
R
ψφψφ
ψφψφ
),tan(),tan( 12112111 rrArrA −−=−−=−⇒
ψφ
Cũng có vô s nghi m trong tr ng h p này.ố ệ ườ ợ
0
4./Đ ng h c ngh chộ ọ ị
(Inverse kinematics)
5