Giaùo aùn Hình hoïc 10NC – Chöông 3
Tiết 40 - 41 §6. ĐƯỜNG HYPEBOL
I. MỤC TIÊU: Giúp học sinh:
1. Về kiến thức:
Nhớ được định nghĩa đường hypebol và các yếu tố xác định đường đó
như: tiêu cự, tiêu điểm, tâm sai, ...
2. Về kỹ năng:
Viết được pt chính tắc của hypebol khi biết các yếu tố xác định hypebol.
Từ pt chính tác của hypebol, thấy được tính chất và chỉ ra được các tiêu
điểm, đỉnh, hai đường tiệm cận của hypebol.
3. Về tư duy:
Biết áp dụng vào bài tập.
4. Về thái độ:
Rèn luyện tính nghiêm túc khoa học.
Xây dựng bài một cách tự nhiên chủ động.
II. CHUẨN BỊ PHƯƠNG TIỆN DẠY HỌC:
Học sinh xem bài trước ở nhà.
Chuẩn bị các bảng nhỏ ghi đề bài và dùng để học sinh trả lời theo nhóm.
III. GỢI Ý VỀ PHƯƠNG PHÁP DẠY HỌC:
Phương pháp mở vấn đáp thông qua các hoạt động điều khiển tư duy.
IV. TIẾN TRÌNH BÀI HỌC VÀ CÁC HOẠT ĐỘNG :
Giaùo aùn Hình hoïc 10NC – Chöông 3
1. Kiểm tra bài cũ và dạy bài mới:
Hoạt động của GV và HS Nội dung cơ bản
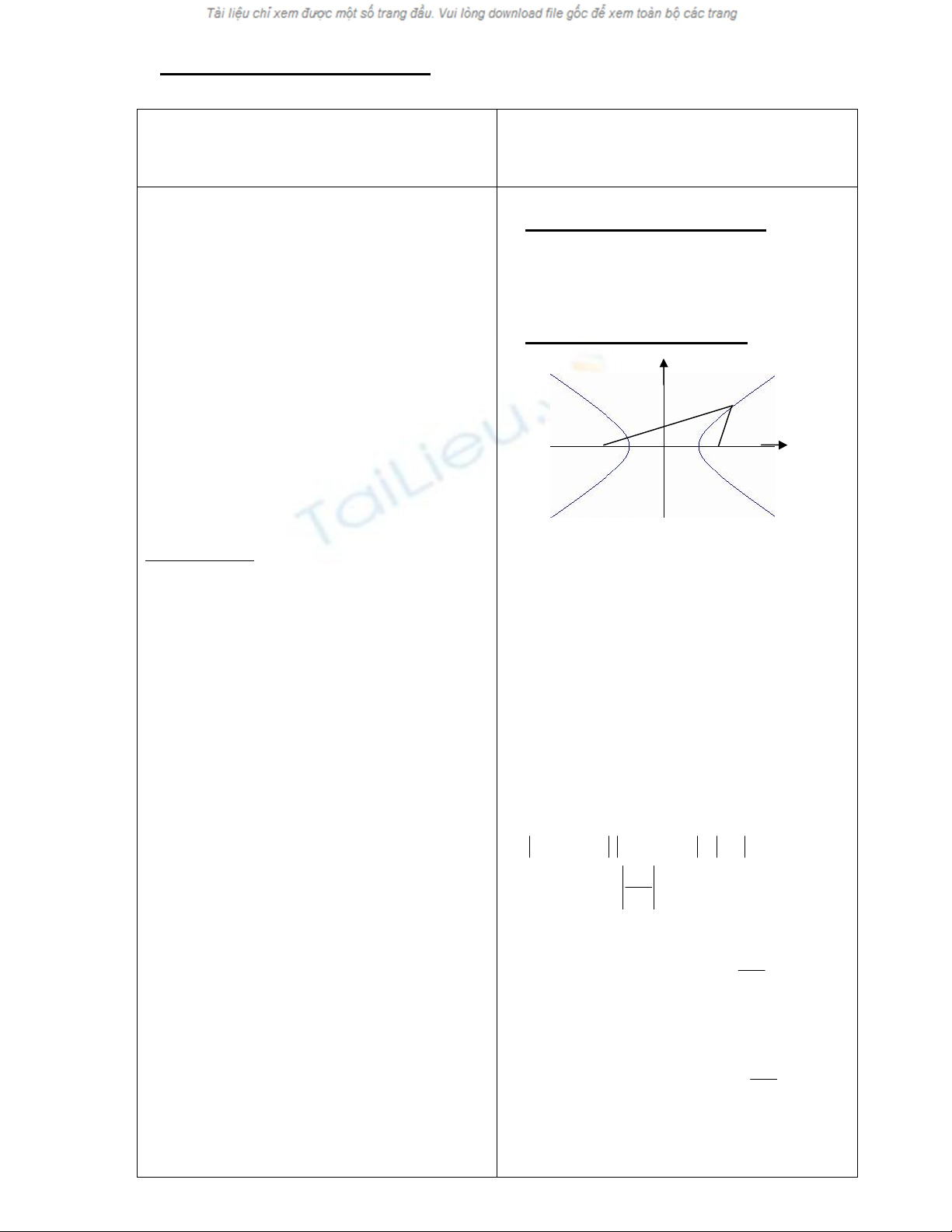
GV vào bài bằng đthị của hàm số y= 1/x
hay chỉ cho hs thấy vùng sáng hắt lên bức
tường từ một đèn bàn (hình 86 sgk)
GV ghi đ/n đương hypebol
Có thể hdẫn hs cách vẽ hypebol như hình
88 sgk, cho hs về nhà thử làm.
Hoạt động 1: Giải bi tốn tìm phương
trình chính tắc của hypebol:
Trước hết ta tính bk qua tiêu của mỗi
điểm M thuộc hypebol.
GV hdẫn hs chọn hệ trục tđộ Oxy (h 89
sgk)
? Em hãy cho biết toạ độ của 2 tiêu điểm
F1 và F2.
GV: gsử
;
M x y H
. Hãy tính biểu
thức
2 2
1 2
MF MF
.
1. Định nghĩa đường hypebol:
Định nghĩa: sgk
2. Pt chính tắc của hypebol:
Ta có:
2 2
2 2 2 2
1 2
2 2
1 2
1 2 1 2
1 2
,
4
. 4
2
MF MF cx
MF MF MF MF cx
cx
MF MF a
Khi x > 0 ta có 1 2
1 2
2
2 ,
cx
MF MF
a
MF MF a
Khi x < 0 ta có 1 2
1 2
2
2 ,
cx
MF MF
a
MF MF a
M(x;y)
F2
F1 O x
y
Giaùo aùn Hình hoïc 10NC – Chöông 3
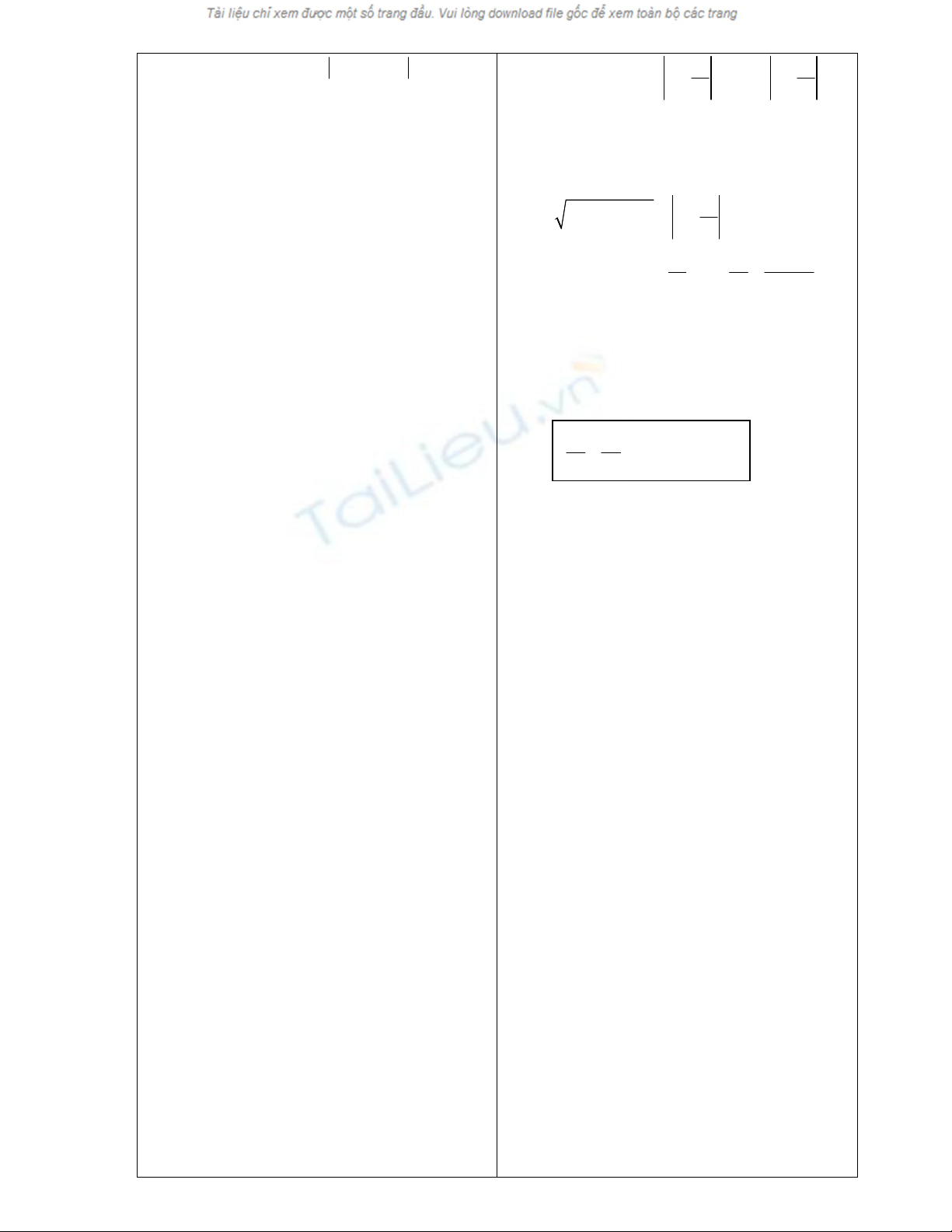
2 2
2 2
1 0, 0
x y a b
a b
GV: hãy sdụng gthiết 1 2
2
MF MF a
để
tính MF1, MF2 = ?
GV: bây giờ ta sẽ lập pt của (H) đối với
hệ toạ độ đã chọn.
M(x;y), F1(-c; 0) => MF1 = ?
Kết hợp với kết quả vừa tìm được ta có:
Bình phương 2 vế và rút gọn đthức ta
được ?
Từ đó suy ra 1 2
,
cx cx
MF a MF a
a a
Ta có:
22
1
22 2
222 2 2
1
cx
MF x c y a a
cx x y
x c y a a a a c
Vì 2 2
0
a c
nên đặt
2 2 2
a c b
hay
2 2 2
, 0
b c a b
, ta đc:
(1)
Ngược lại, có thể CM đc rằng: nếu
M(x;y) thoả (1) thì M thuộc (H).
Pt (1) đgl pt chính tắc của hypebol
Giaùo aùn Hình hoïc 10NC – Chöông 3
Nx: 2 2
? 0
a c
Hoạt động 2:
GV: từ ptct (1) của (H), hãy nêu những
tính chất của hypebol này?
GV nhắc lại ?3 trong §5 (phần elip) để hs
có thể làm tương tự.
Hình vẽ 90 sgk
Yêu cầu hs làm hđ3 trang 107 sgk để hs
có thể hiểu ý nghĩa của “tiệm cận”.
2 2
: 4 4
H x y
, tcận: x – 2y = 0
3. Hình dạng của hypebol:
O là tâm đx; Ox, Oy là 2 trục đx
của(H).
Trục thực nằm trên Ox, độ dài 2a
Trục ảo nằm trên Oy, độ dài 2b
2 đỉnh: (-a;0) và (a;0)
2 tiêu điểm F1(-c;0), F2(c;0)
Tâm sai e = c/a (e >1)
Pt các cạnh của hcn cơ sở
,
x a y b
Pt 2 đường tiệm cận
b
y x
a
Giaùo aùn Hình hoïc 10NC – Chöông 3
K/c từ M0(x0 ; y0) đến đường tcận là
2 2
0 0
0 0
0 0 0 0
4
24
5 5 2 5 2
x y
x y
d
x y x y
Khi x0 > 0 tăng lên thì 2
0 0
1
4
2
y x
cũng
tăng lên, do đó k/c d càng giảm dần.
Cho hs ln bảng lm ví dụ .
Cho học sinh giải ví dụ theo nhóm và
nhận xét cho điểm .
Bk qua tiêu của
M H
:
1
2
M M
M M
c
MF a ex a x
a
c
MF a ex a x
a
VD: Cho hypebol (H): 2 2
1
16 9
x y
Xđịnh toạ độ các đỉnh, các tiêu điểm và
tính tam sai, độ dài trục thực, độ dài trục
ảo của (H).
Hoạt động 3: sửa bt
HS trả lời miệng bài 36. GV
nhận xét và chỉnh sửa.
* Gọi 3 HS lên bảng sửa 3 bài
tập tương ứng:
Hs1: Nêu ptct của (H), hình
dạng của nó và làm bt 37a.
36. Các mđ a), b), d) đúng, mđ c) sai.
37.
a) (H) có a = 3, b = 2, 2 2 2
13 13
c a b c
Tiêu điểm:
1 2
13;0 , 13;0
F F
Độ dài trục thực: 2a = 6
Độ dài trục ảo: 2b = 4
Pt các đường tcận: y = ± 2/3x