Tiết: 40 ĐƯỜNG HYPEBOL
I. Mục tiêu bài dạy:
1.Kiến thức:
Học sinh nắm được định nghĩa đường hypebol và các yếu tố xác định
đường hypebol như : tiêu cự, tiêu điểm, tâm sai,...Học sinh viết được
phương trình chính tắc của hypebol khi biết các yếu tố xác định đường
hypebol. Học sinh thấy được tính chất và chỉ ra được các tiêu điểm, đỉnh, hai
đường tiệm cận của hypebol khi biết phương trình chính tắc của hypebol.
2. Kỹ năng:
Có kỹ năng xác định tiêu cự, tiêu điểm, tâm sai, đỉnh, hai đường tiệm cận
của hypebol khi biết phương trình chính tắc của hypebol. Ngược lại có kỹ
năng lập phương trình chính tắc của hypebol khi biết các yếu tố xác định
đường hypebol.
3. Tư duy:
Hiểu được đường hypebol, phương trình chính tắc của hypebol và các
yếu tố liên quan như : tiêu cự, tiêu điểm, tâm sai, đỉnh, hai đường tiệm cận
của hypebol, ...
4.Thái độ:
Rèn luyện tính tư duy logic trong lập luận. Rèn luyện tính cẩn thận, tỉ
mỉ và chính xác khi tính toán.
II. Chuẩn bị của giáo viên và học sinh:
Giáo viên: tham khảo tài liệu, soạn giáo án, đồ dùng dạy học.
Học sinh: dụng cụ học tập, xem trước bài đường hypebol.
III. Phương pháp:
Đàm thoại, gợi mỡ giải quyết vấn đề và kết hợp hoạt động nhóm.
IV. Tiến trình bài dạy:
1. Bài cũ:
Phát biểu định nghĩa elip và viết phương trình chính tắc của elip.
2. Tiến hành dạy bài mới:
Hoạt Động của GV Hoạt Động của học sinh
Ghi bảng
Hoạt động 1
Đường hypebol là tập
hợp
các điểm thoả mãn tính
chất
gì ?
Định nghĩa đường
hypebol.
1.Định nghĩa:
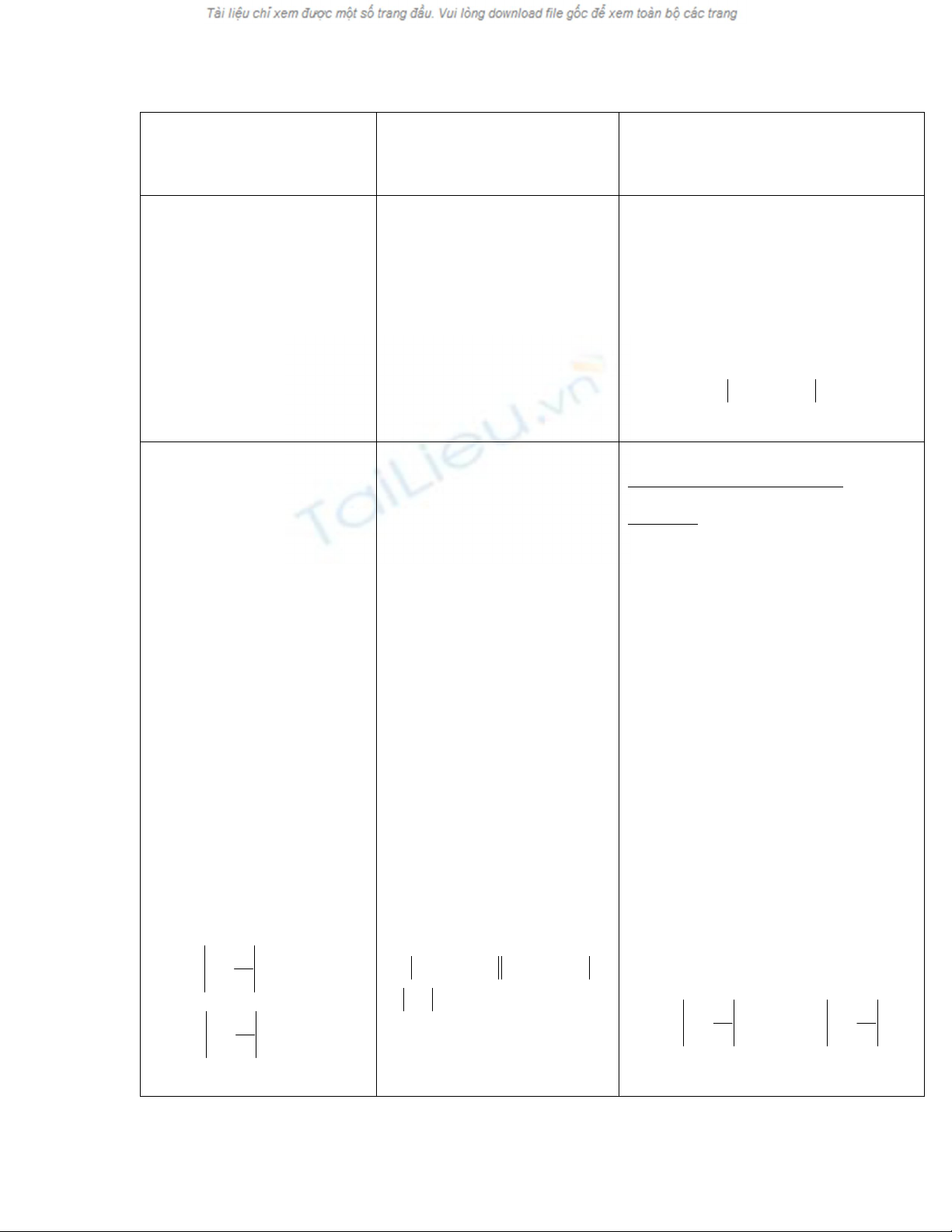
Cho hai điểm cố định F1, F2 có
khoảng cách F1F2 = 2c (c > 0).
Đường hypebol là tập hợp các
điểm M sao cho aMFMF 2
21
(0 < a < c). Hai điểm F1, F2 gọi
M
(H)
F1
F2
Hoạt Động của GV Hoạt Động của học sinh
Ghi bảng
là các tiêu điểm của hypebol.
Khoảng cách F1F2 = 2c gọi là
tiêu cự của hypebol.
aMFMFHM 2)( 21
Hoạt động 2
Chọn hệ toạ độ như thế
nào
để lập phương trình
chính
tắc hypebol ?
Cho học sinh làm nhóm
)();( HyxM
. Hãy tính
2
2
2
1MFMF để suy ra
a
cx
aMF
1,
a
cx
aMF
2
Chọn hệ toạ độ.
Làm việc theo nhóm.
;)( 222
1ycxMF
222
2)( ycxMF
Do đó cxMFMF 4
2
2
2
1
cx
MFMFMFMF
4
2121
2.Phương trình chính tắc
hypebol
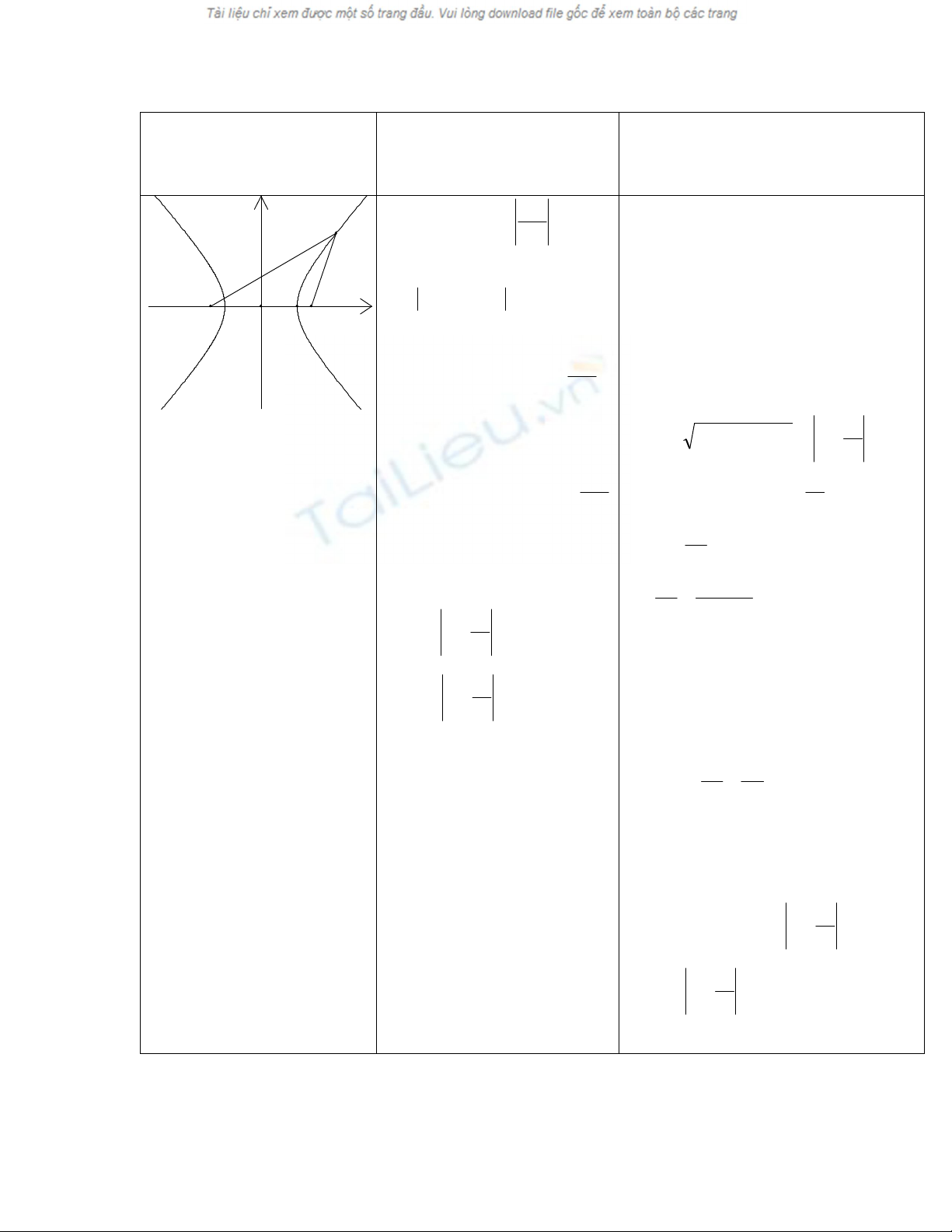
Cho hypebol (H) như định
nghĩa.
Chọn hệ toạ độ Oxy có góc là
trung điểm đoạn thẳng F1F2, trục
Oy là đường trung trực F1F2 và
F2
nằm trên tia Ox. Khi đó F1(-c; 0)
F2(c; 0). Từ đó suy ra
a
cx
aMF
1 và a
cx
aMF
2
Hoạt Động của GV Hoạt Động của học sinh
Ghi bảng
M(x;y)
F2
F1
y
x
o
a
cx
MFMF 2
21
(do aMFMF 2
21 )
aMFMF
a
cx
MFMF
x
2
2
0
21
21
aMFMF
a
cx
MFMF
x
2
2
0
21
21
Từ đó suy ra
a
cx
aMF
1;
a
cx
aMF
2
Các đoạn thẳng MF1, MF2 được
gọi là bán kính qua tiêu của
điểm
M.
1
)1(
)()(
)(
22
2
2
2
2222
2
2
222
22
1
c
a
y
a
x
cayx
a
c
a
cx
aycx
a
cx
aycxMF
Đặt b2 = c2 –a2 (do c >a nên b
>0)
ta được )1)(0,0(1
2
2
2
2 ba
b
y
a
x
Ngược lại nếu điểm M(x;y) thoả
mãn (1) thì a
cx
aMF
1 và
a
cx
aMF
2 do đó
Hoạt Động của GV Hoạt Động của học sinh
Ghi bảng
aMFMF 2
21 , tức là )(HM
Phương trình (1) gọi là phương
trình chính tắc của hypebol.
Trả lời tâm đối xứng (H)
và
trục đối xứng (H).
Gọi tên trục thực, trục
ảo, đỉnh, độ dài trục
thực, độ dài trục ảo,
nhánh, tâm sai, hình
chữ nhật cơ sở, hai
đường tiệm cận
của hypebol.
3.Hình dạng của hypebol
Cho hypebol (H) có phương
trình chính tắc
)1)(0,0(1
2
2
2
2 ba
b
y
a
x
Gốc toạ độ O là tâm đối xứng
(H)
Ox, Oy là hai trục đối xứng (H)
Trục Ox gọi là trục thực, trục Oy
gọi là trục ảo. Hai giao điểm của
(H) với trục Ox gọi là hai đỉnh.
Khoảng cách 2a giữa hai đỉnh
gọi