GÍA TRỊ CỦA BIẾN ĐỂ XẢY RA ĐẲNG THỨC
HOẶC BĐT CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI
1/Phương pháp chung :
Để tìm giá trị của biến trong đẳng thức hoặc Bất đẳng thức chứa dấu giá trị
tuyệt đối là xét các khoảng giá trị của biến để lập bảng xét dấu rồi khử dấu
giá trị tuyệt đối .
Ví dụ 16: Tìm x .Biết rằng :
a/ 631 xx (1)
GIẢI:
Xét x-1 = 0 <=>x = 1 và xét x-3 = 0 <=> x = 3
x-1< 0 <=> x < 1 x-3 < 0 <=> x < 3
x-1> 0 <=> x > 1 x-3 > 0 <=> x > 3
Ta có bảng xét dấu các đa thức x-1 ; x-3 như sau :
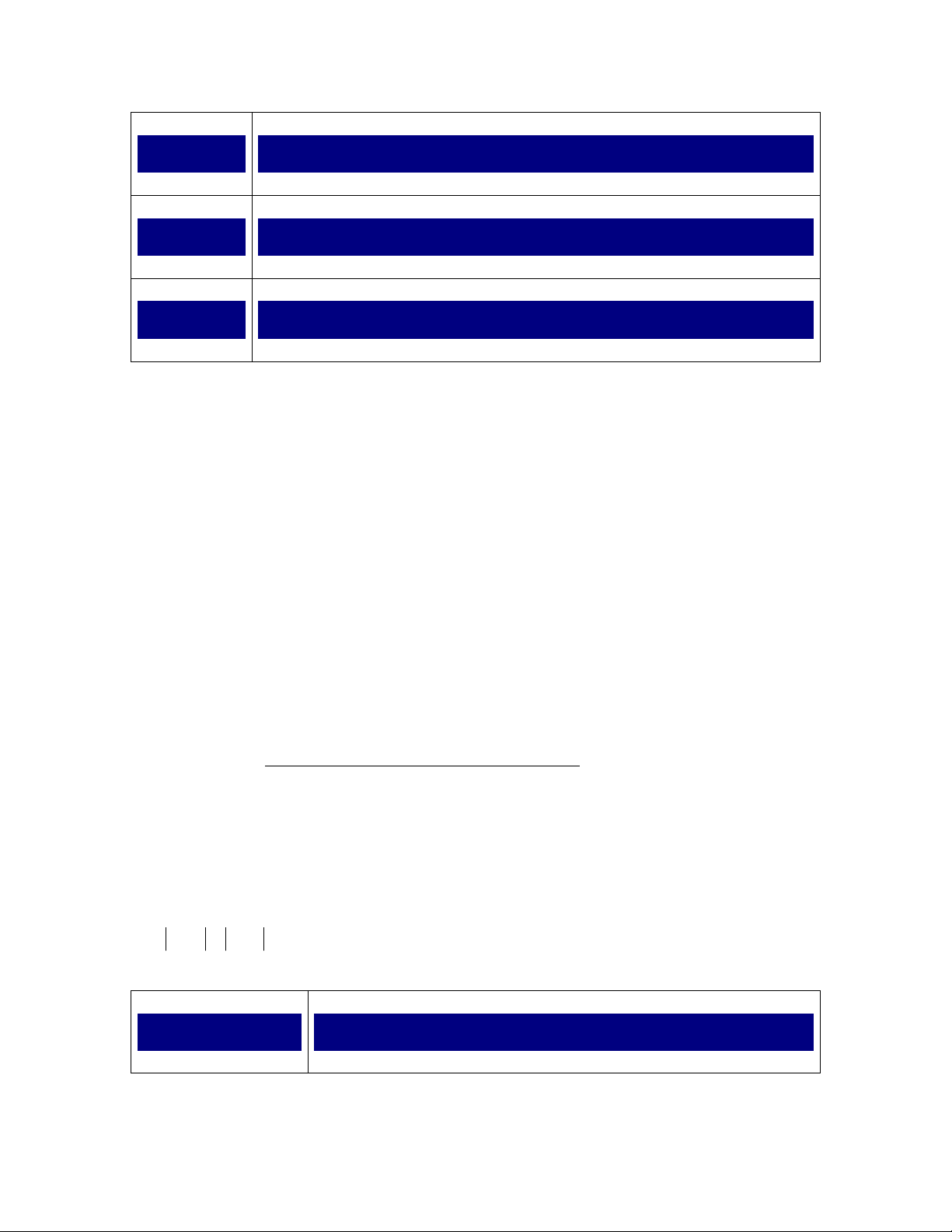
x 1 3
x - 1 - 0 + / +
x - 3 - / - 0 +
Đẳngthức (1) (-x+1)+(-x+3)=6 (x-1)+(3-x)= 6 (x-1)+(x-3) = 6
-2x=2 0x = 4 2x = 10
x=-1 (không có giá trị x = 5
(giá trị nầy thuộc nào thoả mãn (1) ( giá tri nầy thuộc
khoảng đang xét) khoảng đang xét)
Vậy x = -1 và x = 5 thì thoả mãn (1)
b/ 752 xx
x -2 5
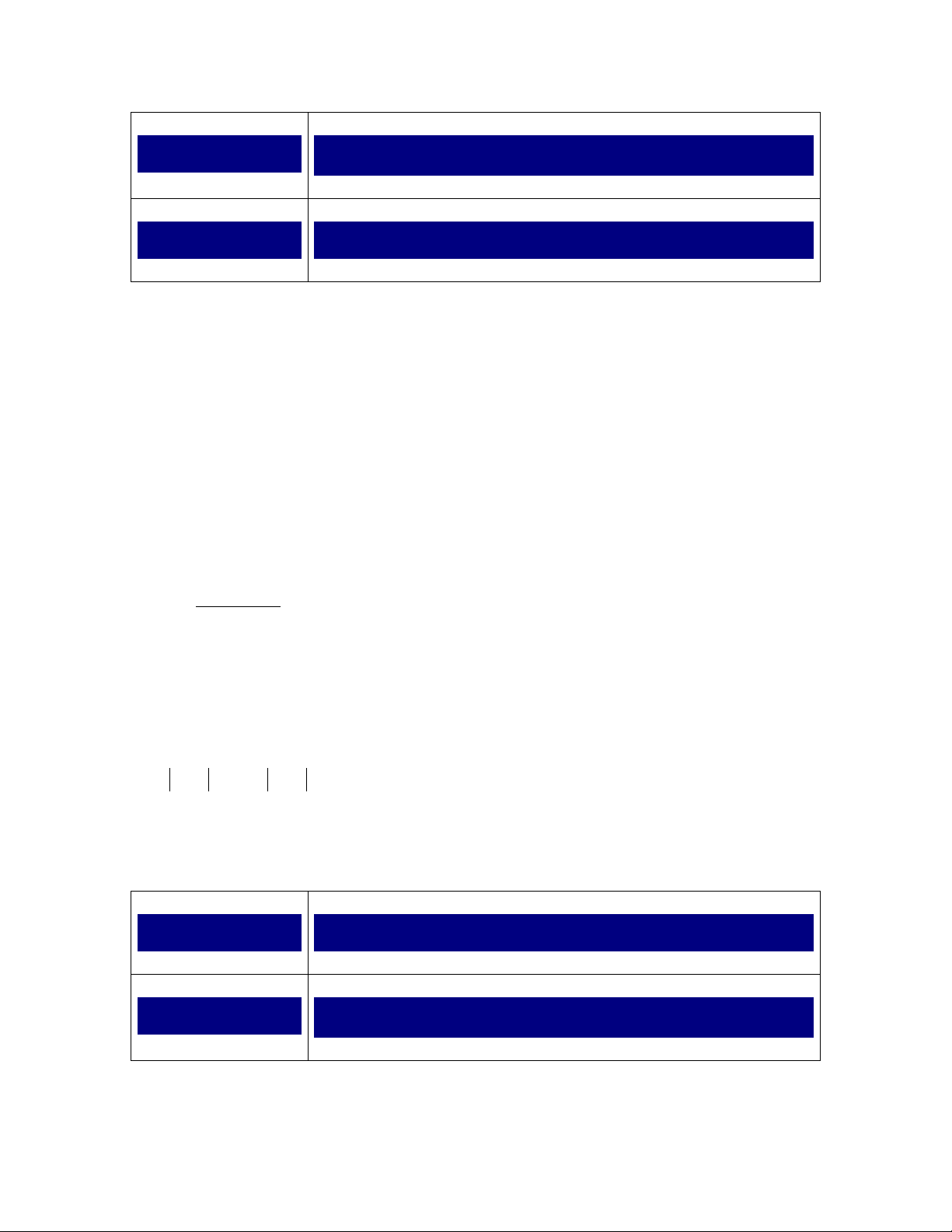
x+2 - 0 + / +
x-5 - / - 0 +
* Xét khoảng x <2 Ta được -2x = 4 <=> x= -2 (loại)
Xét khoảng-2 5
x Ta được 0x = -0 đúng với mọi x trong khoảng
đang xét . Vậy -2 5
x
Xét khoảng x >5 Ta đựoc 2x=10 <=> x = 5 ( loại)
Kết luận: -2 5
x
c/ 423 xxx
x -3 4
x+3 - 0 + / +
x- 4 - / - 0 +
*Xét khoảng x < 3 ta được -2x = 7 <=> x= -3,5( thuộc khoảng đang xét)
*Xét khoảng -3 4
x ta được 0x = 1=> không có giá trị nào của x thoả
mãn.
* Xét khoảng x>4 Ta được -2x = -7 <=>x = 3,5 không thuộc khoảng
đang xét .
Kết luận : vậy x = -3,55
Ví dụ 17: Tìm x , Biết: 131 xxx (2)
Tương tự:
Xét khoảng x< 1 Ta có (2) =>(1-x)+*3-x)<x+1<=>-3x<-3<=>x>1(
Giá trị nầy không thuộc khooảng đang xét)
Xét khoảng 1 3
x thì (2)=>(x-1)+(3-x)<x+1<=>2<x+1<=>x>1 =>
Ta có các giá trị 1<x 3
(3)
Xét khoảng x >3 => ta có (x-1)+(x-3)<x+1<=>x<5.
Ta có các giá trị : 3<x<5 (4)
Kết luận: Từ (3) và (4) các giá trị cần tìm là : 3<x<5
2/ Sau đây ta xét một số dạng đặc biệt. Trong những dạng nầy;
để tìm x ngoài phương pháp chung đã nêu ở trên ta có thể giải
bằng cách khác đơngiản hơn.
Dạng 1 )(xf = a ( a là hằng số dương) <=>f(x)=
a
Dạng 2 )(xf = g(x) <=>1/g(x) 0
& 2/f(x)= )(xg
Dạng 3 )(xf )(xg hay )(xf -)(xg = 0 <=>f(x)= )(xg
Dạng 4 )(xf + )(xg = 0 <=> f(x)=0 và g(x) = 0