GIẢI BÀI TOÁN BẰNG ĐẠI LƯỢNG TỈ LỆ
Các em học sinh thân mến ! Trong chương trình toán 4 các em đã làm quen với hai
bài toán về đại lượng tỉ lệ thuận và đại lượng tỉ lệ nghịch và đã được biết thế nào là
đại lượng tỉ lệ thuận và tỉ lệ nghịch. Việc áp dụng các quan hệ đó để giải một số bài
toán đã được thông qua các bài học. ở đây chúng tôi muốn đưa thêm một số ví dụ
khác có thể áp dụng đại lượng tỉ lệ để giải. Hi vọng các em sẽ tìm thấy những điều
mới lạ và hấp dẫn trong cách giải các bài toán đó.
Ví dụ 1 : Hưng đi xe đạp từ nhà lên huyện với vận tốc 12 km/giờ. Sau đó trở về
với vận tốc 10 km/giờ. Tính quãng đường từ nhà lên huyện biết rằng thời gian lúc
về lâu hơn lúc đi là 10 phút.
Nhận xét : Ta thấy Hưng đi và về trên cùng một đoạn đường từ nhà lên huyện. Do
đó thời gian đi và về sẽ tỉ lệ nghịch với vận tốc lúc đi và vận tốc lúc về. ở đây tỉ số
về vận tốc giữa lúc đi và lúc về là 12/10 = 6/5. Vậy tỉ số giữa thời gian đi và thời
gian về là 5/6. Mà thời gian lúc về lâu hơn lúc đi là 10 phút hay nhiều hơn 10 phút.
Từ đó ta có sơ đồ :
Thời gian lúc về hết là :
10 : (6 - 5) x 6 = 60 (phút)
Đổi : 60 phút = 1 giờ
Quãng đường từ nhà lên huyện là :
10 x 1 = 10 (km)
Đáp số : 10 km.
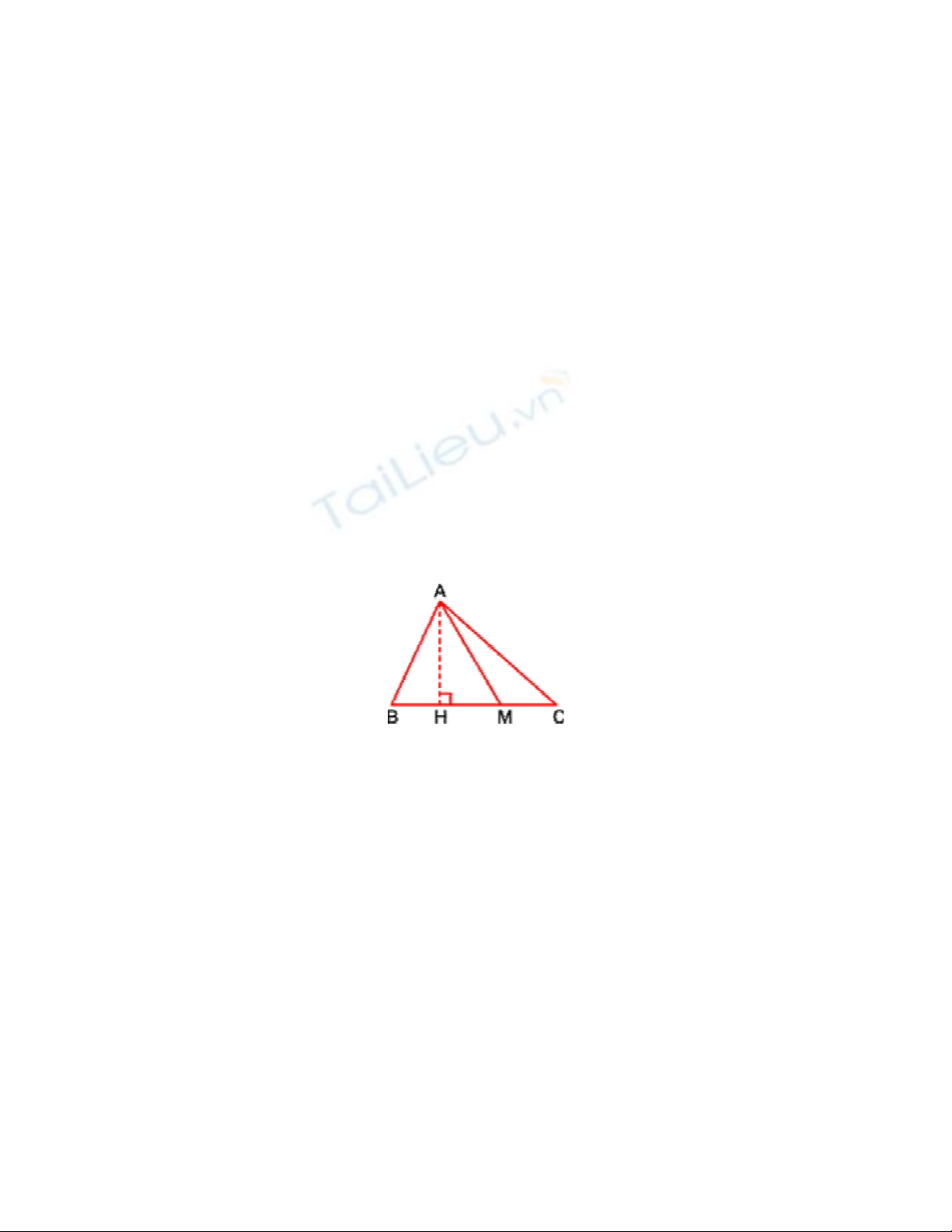
Ví dụ 2 : Cho tam giác ABC có diện tích 75 cm2. Trên BC lấy M sao cho BM =
2/3 BC. Tính diện tích tam giác ABM.
Nhận xét : Ta thấy tam giác ABM và tam giác ABC có cùng chiều cao là AH ; hai
đáy tương ứng là BM và BC. Do đó đáy và diện tích là hai đại lượng tỉ lệ thuận với
nhau.
ở đây tỉ số về hai đáy là : BM/BC = 2/3. Vậy tỉ số về diện tích của hai tam
giácABM và ABC là 2/3. Vì diện tích tam giác ABC bằng 75 cm2, nên diện tích
tam giác ABM là :
75 : 3 x 2 = 50 (cm2).
Đáp số : 50 cm2.
Ví dụ 3 : Cô giáo xếp chỗ ngồi cho học sinh lớp 4A. Nếu xếp mỗi bàn 4 bạn thì
thiếu một bàn. Nếu xếp mỗi bàn 5 bạn thì thừa một bàn. Hỏi lớp đó có bao nhiêu
bàn, bao nhiêu học sinh ?
Nhận xét : Số học sinh không đổi nên số bàn và số học sinh xếp ở mỗi bàn là hai
đại lượng tỉ lệ nghịch với nhau.
Số bàn cần có để xếp 4 bạn 1 bàn nhiều hơn số bàn cần có để xếp 5 bạn 1 bàn là : 1
+ 1 = 2 (bàn)
ở đây tỉ số giữa số bạn xếp ở một bàn 4 bạn và một bàn 5 bạn là . Do đó tỉ số giữa
số bàn khi xếp một bàn 4 bạn và một bàn 5 bạn là .
Vậy ta có sơ đồ :
Số bàn cần đủ để xếp 4 bạn một bàn là : 2 : (5 - 4) x 5 = 10 (bàn)
Số bàn lớp 4A là : 10 - 1 = 9 (bàn)
Số học sinh lớp 4A là : 4 x 9 + 4 = 40 (học sinh)
Đáp số : 9 bàn ; 40 học sinh.
Các em thấy không ? Đó mới chỉ là 3 ví dụ, ngoài ra còn nhiều ví dụ khác nữa, hi
vọng các em sẽ áp dụng đại lượng tỉ lệ để giải một cách tốt hơn. Sau đây là một số
bài toán để các em làm thử :
1. Một hình chữ nhật có chiều dài gấp 4 lần chiều rộng. Hỏi nếu tăng chiều dài
thêm một đoạn bằng chiều rộng thì chiều rộng sẽ thay đổi như thế nào để diện tích
hình đó không thay đổi.
2. Đội tuyển học sinh giỏi có số bạn nam gấp 3 lần số bạn nữ. Thầy giáo nhẩm tính
rằng nếu thay 3 bạn nam bằng 3 bạn nữ thì số bạn nam chỉ nhiều hơn số bạn nữ là
6 bạn. Hỏi đội tuyển đó có bao nhiêu bạn nam, bao nhiêu bạn nữ.
3. Ba tổ trồng được tất cả 120 cây. Biết rằng số cây của tổ 1 và tổ 2 trồng được
nhiều hơn số cây trồng được của tổ 2 và tổ 3 là 10 cây. Số cây của tổ 2 và tổ 3
trồng được ít hơn số cây của tổ 3 và tổ 1 trồng được là 5 cây. Tính số cây mỗi tổ
trồng được.