Khaûo saùt öùng duïng MATLAB trong ñieàu khieån töï ñoäng
Thöïc hieän: PHAÏM QUOÁC TRÖÔØNG - 6 - GVHD: PHAÏM QUANG HUY
2 4
dc = 1
5. Leänh SS2TF
a) Coâng duïng:
Chuyeån heä thoáng töø daïng khoâng gian traïng thaùi thaønh daïng haøm truyeàn.
b) Cuù phaùp:
[num,den] = ss2tf(a,b,c,d,iu).
c) Giaûi thích:
[num,den] = ss2tf(a,b,c,d,iu) chuyeån heä thoáng khoâng gian traïng thaùi:
⎪
⎩
⎪
⎨
⎧
+=
+=
DuCxy
BuAxx
.
thaønh daïng haøm truyeàn:
H(s) = )(
)(
sden
sNUM = C(sI – A)-1 B + D
töø ngoõ vaøo thöù iu. Vector den chöùa caùc heä soá cuûa maãu soá theo chieàu giaûm daàn soá muõ cuûa
s. Ma traän NUM chöùa caùc heä soá töû soá vôùi soá haøng laø soá ngoõ ra.
d) Ví duï:
Haøm truyeàn cuûa heä thoáng ñöôïc xaùc ñònh baèng leänh:
[num,den] = ss2tf (a,b,c,d,1)
ta ñöôïc:
num =
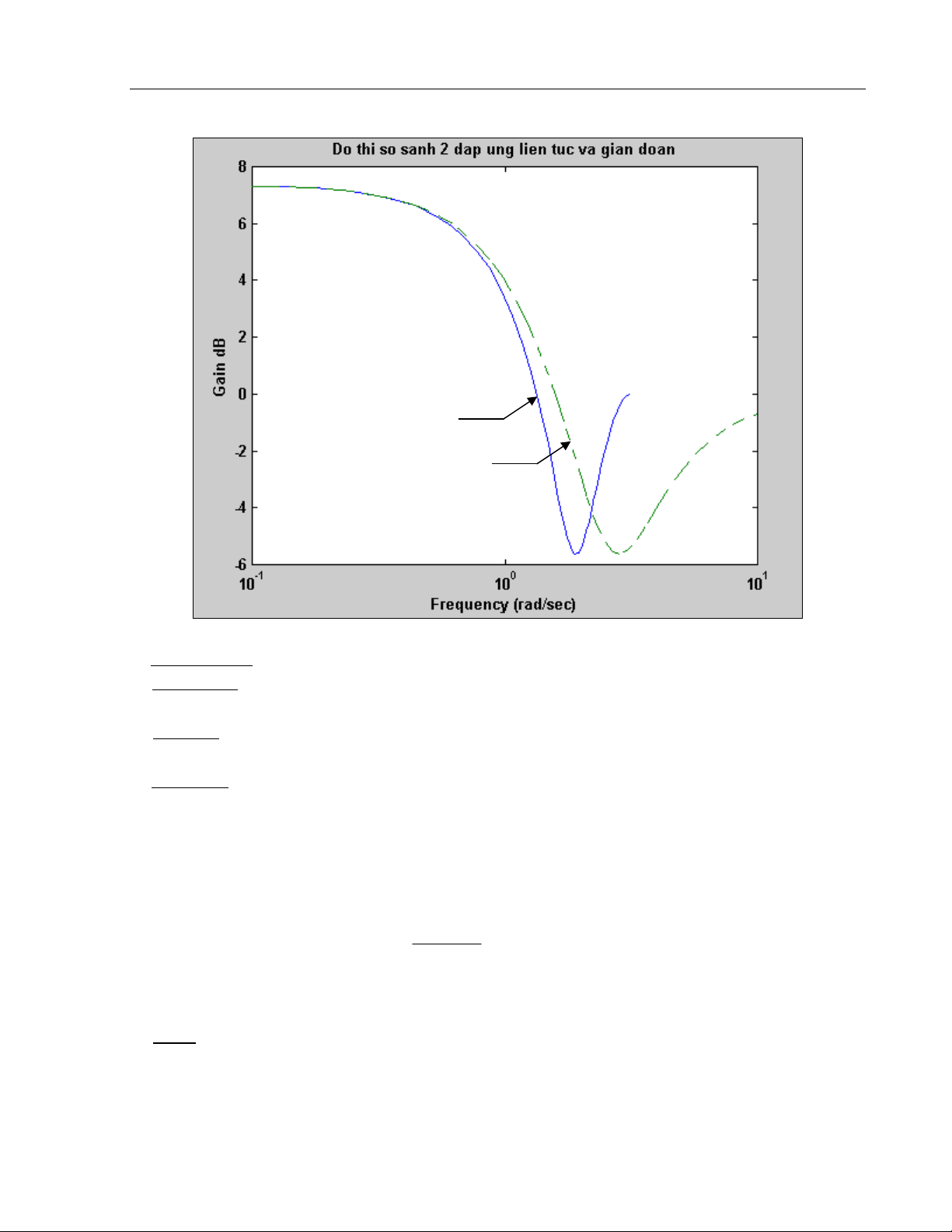
Ñaùp öùng giaùn ñoaïn
Ñaùp öùng lieân tuïc
Khaûo saùt öùng duïng MATLAB trong ñieàu khieån töï ñoäng
Thöïc hieän: PHAÏM QUOÁC TRÖÔØNG - 7 - GVHD: PHAÏM QUANG HUY
0 0 1.0000
den =
1.0000 0.4000 1.0000
6. Leänh TF2SS
a) Coâng duïng:
Chuyeån heä thoáng töø daïng khoâng gian haøm truyeàn thaønh daïng traïng thaùi.
b) Cuù phaùp:
[a,b,c,d] = tf2ss(num,den)
c) Giaûi thích:
[a,b,c,d] = tf2ss(num,den) tìm heä phöông trình traïng thaùi cuûa heä SISO:
.
x= Ax + Bu
y = Cx + Du
ñöôïc cho bôûi haøm truyeàn:
töø ngoõ vaøo duy nhaát. Vector den chöùa caùc heä soá maãu soá haøm truyeàn theo chieàu giaûm daàn
soá muõ suûa s. Ma traän NUM chöùa caùc heä soá cuûa töû soá vôùi soá haøng laø soá ngoõ ra y. Caùc ma
traän a, b, c, c trôû thaønh daïng chính taét.
* Ví duï 1:
Xeùt heä thoáng coù haøm truyeàn:
Ñeå chuyeån heä thoáng thaønh daïng khoâng gian traïng thaùi ta thöïc hieän caùc leänh:
Num = [0 2 3
1 2 3];
den = [1 0.4 1];
[a,b,c,d] = tf2ss (num,den);
ta ñöôïc keát quaû:
a =
-0.4000 -1.0000
1.0000 0
b =
1
0
c =
2.0000 3.0000
1.0000 2.0000
d =
0
1
DBA)-C(sI
den(s)
NUM(s)
H(s) 1- +==
1s4.0s
12ss
32s
H(s) 2
2
+
+
⎥
⎦
⎤
⎢
⎣
⎡
++
+
=
Khaûo saùt öùng duïng MATLAB trong ñieàu khieån töï ñoäng
Thöïc hieän: PHAÏM QUOÁC TRÖÔØNG - 8 - GVHD: PHAÏM QUANG HUY
Ví duï 2: Trích töø saùch ‘ÖÙng duïng MATLAB trong ñieàu khieån töï ñoäng’ taùc giaû Nguyeãn Vaên
Giaùp.
Cho haøm truyeàn: (s2+7s +2) / (s3+9s2+26s+24)
» num=[1 7 2];
» den=[1 9 26 24];
» [A,B,C,D]=tf2ss(num,den)
Keát quaû:
A =
-9 -26 -24
1 0 0
0 1 0
B =
1
0
0
C =
1 7 2
D =
0
7. Leänh SS2ZP
a) Coâng duïng:
Khaûo saùt öùng duïng MATLAB trong ñieàu khieån töï ñoäng
Thöïc hieän: PHAÏM QUOÁC TRÖÔØNG - 9 - GVHD: PHAÏM QUANG HUY
Chuyeån heä thoáng khoâng gian sang traïng thaùi ñoä lôïi cöïc-zero (zero pole-gain)
b) Cuù phaùp:
[z,p,k] = ss2zp(a,b,c,d,iu)
c) Giaûi thích:
ss2zp tìm caùc zero, cöïc vaø ñoä lôïi khoâng gian traïng thaùi.
[z,p,k] = ss2zp(a,b,c,d,iu) tìm haøm truyeàn döôùi daïng thöøa soá.
))((.....))2(()1((
))((.....))2(()1((
)(
)(
)( npspsps
mZsZsZs
k
sp
sZ
sH −−−
−
−
−
==
cuûa heä thoáng:
BuAxx +=
.
y = Cx + Du
töø ngoõ vaøo thöù iu. Vector coät p chöùa caùc cöïc maãu soá haøm truyeàn. Caùc zero cuûa töû soá naèm
trong caùc coät cuûa ma traän z vôùi soá coät laø soá ngoõ ra y. Ñoä lôïi cuûa töû soá haøm truyeàn naèm trong
caùc coät vector k.
d) Ví duï:
Xeùt heä thoáng coù haøm truyeàn:
14.0
32
)( 2++
+
=
ss
s
sH
num = [2 3];
den = [1 0.4 1];
Coù 2 caùch ñeå tìm caùc zero, cöïc vaø ñoä lôïi cuûa heä thoáng naøy:
+ Caùch 1:
[z,p,k] = tf2zp(num, den)
+ Caùch 2:
[a,b,c,d] = tf2ss(num, den);
[z,p,k] = ss2zp(a,b,c,d,1)
vaø ta ñöôïc cuøng moät keát quaû nhö sau:
z = -1.5000
p = -0.2000 + 0.9798i
-0.2000 – 0.9798I
k = 2.0000
8. Leänh ZP2SS:
Khaûo saùt öùng duïng MATLAB trong ñieàu khieån töï ñoäng
Thöïc hieän: PHAÏM QUOÁC TRÖÔØNG - 10 - GVHD: PHAÏM QUANG HUY
a) Coâng duïng:
Chuyeån töø ñoä cöïc lôïi zero sang heä khoâng gian traïng thaùi.
b) Cuù phaùp:
[a,b,c,d] = zp2ss(z,p,k)
c) Giaûi thích:
zp2ss hình thaønh moâ hình khoâng gian traïng thaùi töø caùc zero, cöïc vaø ñoä lôïi cuûa heä thoáng
döôùi daïng haøm truyeàn.
[a,b,c,d] = zp2ss(z,k,p) tìm heä khoâng gian traïnng thaùi:
BuAxx +=
.
y = Cx + Du
cuûa heä SIMO ñöôïc cho bôûi haøm truyeàn:
))((.....))2(()1((
))((.....))2(()1((
)(
)(
)( npspsps
mZsZsZs
k
sp
sZ
sH −−−
−
−
−
==
Vector coät p chöùa caùc cöïc vaø ma traän z chöùa caùc zero vôùi soá coät laø soá ngoõ ra. Vector k
chöùa caùc heä soá ñoä lôïi.Caùc ma traän a,b,c,d trôû veà daïng chính taéc.
9. Leänh TF2ZP
a) Coâng duïng:
Chuyeån heä thoáng töø daïng haøm truyeàn sang daïng ñoä lôïi cöïc-zero.
b) Cuù phaùp:
[z,p,k] = tf2zp (NUM,den)
c) Giaûi thích:
tf2ss tìm caùc zero, cöïc vaø ñoä lôïi cuûa heä thoáng ñöôïc bieåu dieãn döôùi daïng haøm truyeàn.
[z,p,k]= tf2zp (NUM,den) tìm haøm truyeàn cuûa heä SIMO daïng:
))((.....))2(()1((
))((.....))2(()1((
)(
)(
)( npspsps
mZsZsZs
k
sp
sZ
sH −−−
−
−
−
==
ñöôïc cho bôûi haøm truyeàn:
)()1(.....)1(
)()1(.....)1(
)(
)(
1
1
nddensnddensden
nnNUMsnnNUMsNUM
sden
sNUM
nd
nn
+−++
+−++
=−
−
Vector den chöùa caùc heä soá cuûa maãu soá theo chieàu giaûm daàn soá muõ cuûa s. Ma traän NUM
chöùa caùc heä soá töû soá vôùi soá haøng laø soá ngoõ ra. Ma traän z chöùa caùc zero, vector coät p chöùa caùc
cöïc vaø vector k chöùa caùc heä soá ñoä lôïi cuûa haøm truyeàn.