Ch−¬ng 4 - §å ho¹ hai chiÒu
PhÇn 1 - C¬ së 67
c
c.
.
V
VÏ
Ï
h
ho
o¹
¹t
t
h
h×
×n
nh
h
(
(
c
co
om
me
et
t
)
)
LÖnh comet plot cho phÐp ng−êi sö dông vÏ theo tõng ®iÓm trªn mμn h×nh
g©y hiÖu øng ho¹t ho¹ khi vÏ. D−íi ®©y lμ mét sè trong bé lÖnh comet.
Comet (x, y) VÏ vector y trªn trôc x. NÕu tham sè vμo kh«ng cã hay
thiÕu th× ch−¬ng tr×nh tù ®Þnh ra chØ sè
Comet (x, y, l) VÏ theo hμm comet víi phÇn kÐo dμi l khi kh«ng khai
b¸o chØ sè l th× ch−¬ng tr×nh tù lÊy gi¸ trÞ = 0.1
d
d.
.H
Hμ
μm
m
®
®å
å
h
ho
o¹
¹.
.
fplot (fku,lim,str) Dïng ®Ó vÏ mét hμm to¸n häc bÊt kú ®−îc khai b¸o
bëi m¶ng ký tù. M¶ng ký tù cã thÓ lμ c¸c hμm chuÈn hay
®−îc ®Þnh nghÜa bëi ng−êi sö dông trong file M fku.m.
Vector lim = [Xmin Xmax] dïng ®Ó giíi h¹n
kho¶ng x¸c ®Þnh cña ®å ho¹. Nã cã thÓ bao gåm 4 thμnh
phÇn trong ®ã thμnh phÇn thø 3 vμ 4 lμ kho¶ng x¸c ®Þnh
trªn trôc y. NÕu biÕn str kh«ng khai b¸o trong hμm th×
ch−¬ng tr×nh sÏ tù lÊy c¸c gi¸ trÞ mÆc ®Þnh vÒ kiÓu ®−êng
hay mÇu cho phÇn ®å ho¹.
fplot
( fcu, lim, str, tol )
VÏ ®å thÞ nh− trªn víi sai sè liªn quan nhá h¬n gi¸ trÞ
tol
VÝ dô:
Dïng hμm fplot vÏ ph−¬ng tr×nh sin x2
>> fplot(‘ sin(x^2)’,[ 0 , 10 ] );
H
H×
×n
nh
h
4
4.
.1
16
6
P
Ph
h−
−¬
¬n
ng
g
t
tr
r×
×n
nh
h
s
si
in
n
x
x2
2
q
qu
ua
a
h
hμ
μm
m
f
fp
pl
lo
ot
t(
()
)
4
4.
.3
3.
.2
2.
.C
C¸
¸c
c
h
hÖ
Ö
t
to
o¹
¹
®
®é
é
t
tr
ro
on
ng
g
m
mÆ
Æt
t
p
ph
h¼
¼n
ng
g
-0.5
0
0.5
1
Ch−¬ng 4 - §å ho¹ hai chiÒu
PhÇn 1 - C¬ së 68
Hμm plot cho phÐp ng−êi sö dông vÎtªn to¹ ®å §Ò c¸c. Tuy nhiªn 1 sè bμi
to¸n trong kü thuËt l¹i yªu cÇu c¸c hÖ to¹ ®é kh¸c. §Ó ®¸p øng nhu cÇu ®ã Matlab
cung cÊp 1 lo¹t c¸c hμm cho phÐp t¹o dùng ®å häa trªn c¸c lo¹i hÖ to¹ ®é.
polar ( thet, r ) - VÏ trªn hÖ täa ®é cùc. C¸c phÇn tõ cña vector theta lμ
c¸c biÕn ®o b»ng radian vμ c¸c phÇn tö cña vector r lμ
kho¶ng c¸ch ®Õn ®iÓm gèc.
semilogx ( x, y ) - Cho phÐp vÏ trªn hÖ to¹ ®é nöa trôc loga, thay log10
®−îc sö dông cho trôc x. §iÒu ®ã còng t−¬ng ®−¬ng víi
viÖc chóng ta viÕt plot (log10(x,y) nh−ng sÏ kh«ng cã lçi
víi c¶ trong tr−êng hîp log10(0).
semilogy ( x,y ) - VÏ trªn hÖ to¹ ®é cña trôc loga. Thang ®o log10 ®−îc
sö dông cho trôc y. §iÒu ®ã t−¬ng ®−¬ng plot (x,log10(y)
vμ còng sÏ kh«ng b¸o lçi khi viÕt log10(0).
loglog ( x,y ) - Hμm cho phÐp vÏ trªn hÖ to¹ ®é loga 2 trôc cña hÖ
to¹ ®é ®Òu dùa trªn thang ®o log10. §iÒu ®ã t−¬ng ®−¬ng
víi viÖc plot(log10(x), log10(y)) vμ còng kh«ng b¸o lçi nÕu
ta sö dông log10(0).
VÝ dô: a)
>> x = linespace (0,7); % t¹o gi¸ trÞ x
>> y = exp(x) % t¹o y theo x
>> subplot (x,1,1); plot( x,y ); % vÏ hμm chuÈn
>> subplot(2,1,2); semilogy( x,y ); % vÏ hμm loga
H
H×
×n
nh
h
4
4.
.1
16
6
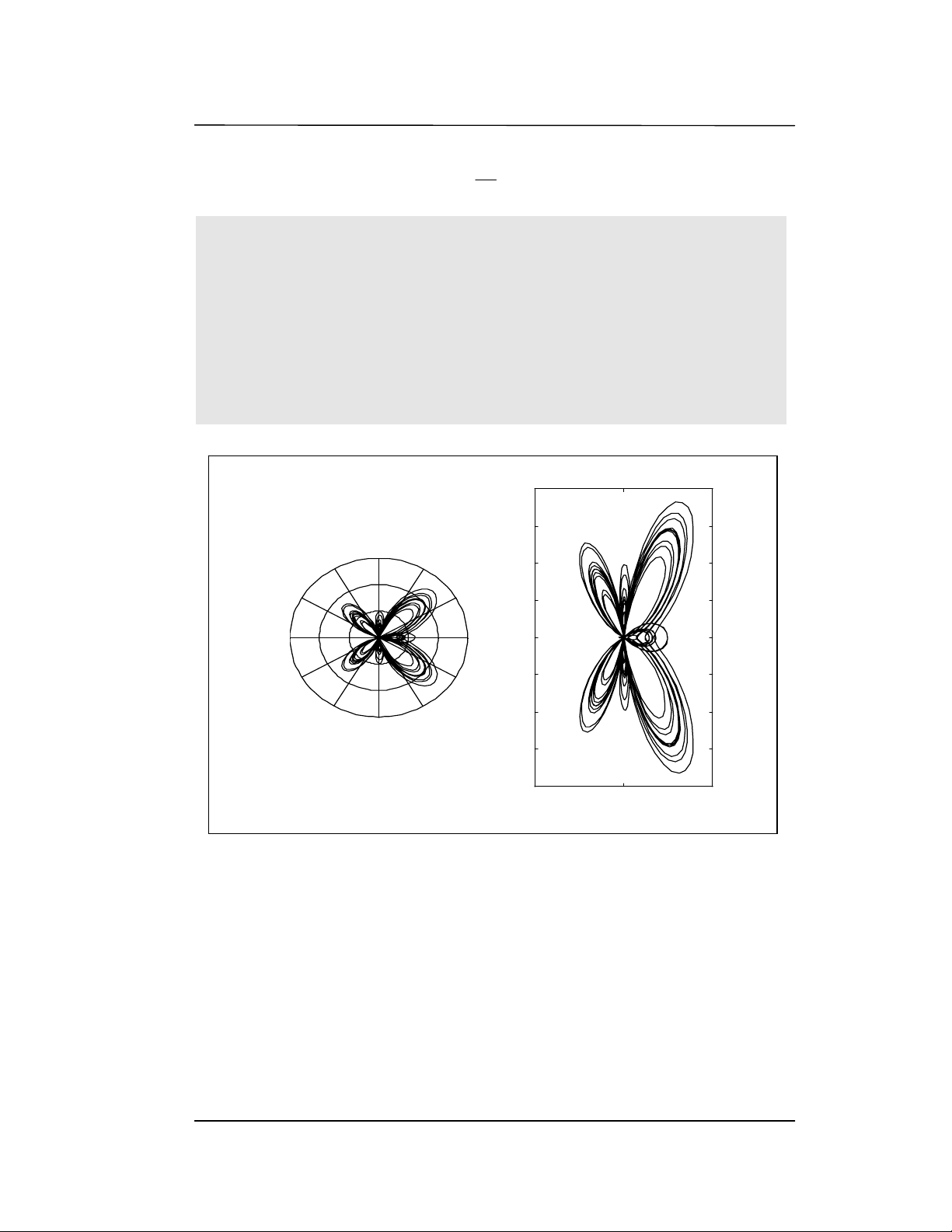
b)VÏ hμm sau trªn hª to¹ ®é cùc theo c«ng thøc sau:
400
600
800
1000
1200
101
102
103
104
Ch−¬ng 4 - §å ho¹ hai chiÒu
PhÇn 1 - C¬ së 69
R = ecost - 2cos4 + sin t5
12
⎛
⎝
⎜⎞
⎠
⎟
>> t = linspace (0,22*pi,1100);
>> r = exp ( cos( t ) ) - 2*cos (u*t)+sin ( t./12) ).^5;
>> subplot (2,1,1);
>> p = polar(t,r); % vÏ trªn hÖ to¹ ®é cùc
>> subplot (2,1,2)
>> [ x , y ] = pol2cart(t,r) % gi¸ trÞ tõ hÖ to¹ ®é cùc sang hÖ §Ò c¸c
>> plot(x,y); % polar_to_carttesian
H
H×
×n
nh
h
4
4.
.1
17
7
t
tr
rª
ªn
n
h
hÖ
Ö
t
to
o¹
¹
®
®é
é
c
cù
ùc
c
4
4.
.3
3.
.3
3.
.
M
MÆ
Æt
t
p
ph
h¼
¼n
ng
g
®
®å
å
h
ho
o¹
¹
c
ch
ho
o
s
sè
è
p
ph
hø
øc
c.
.
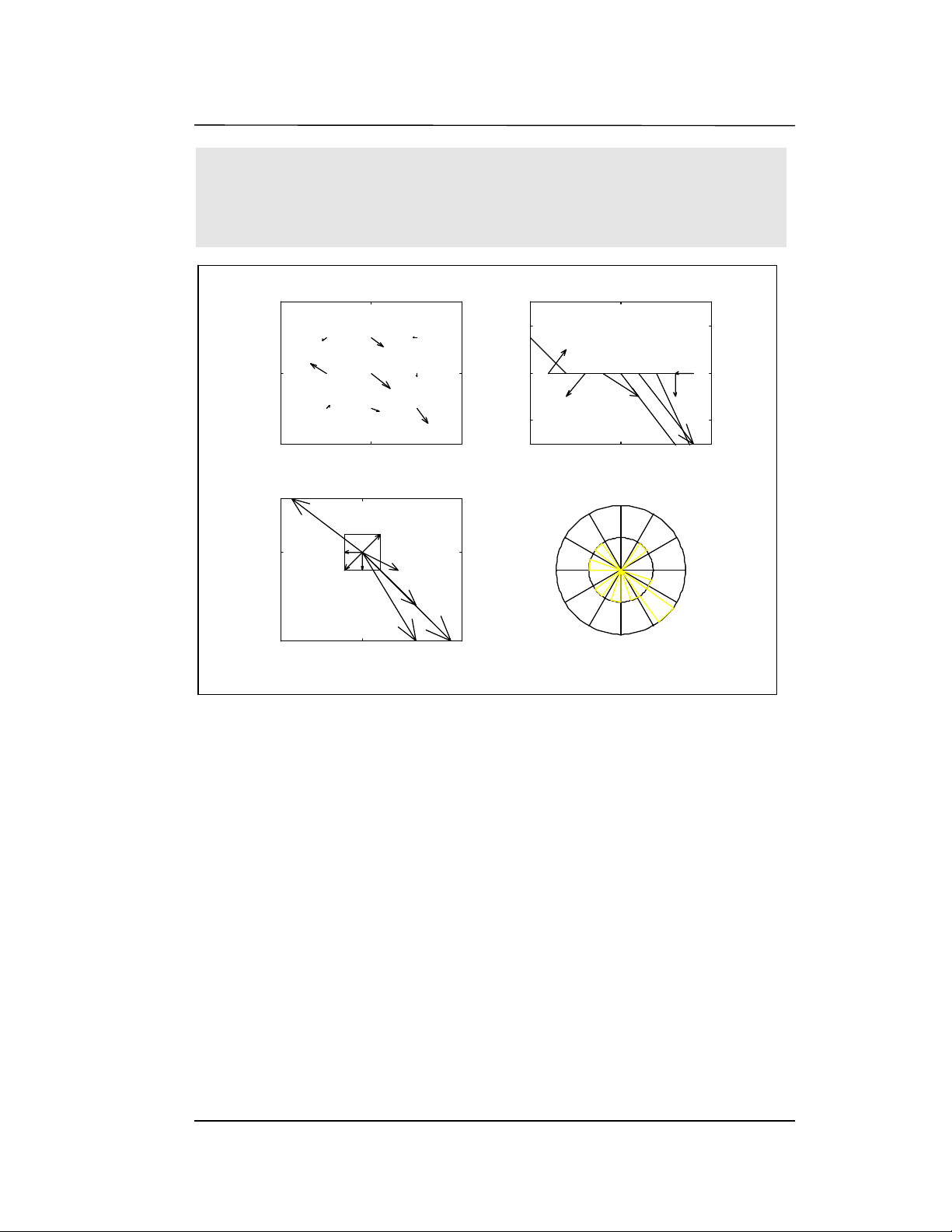
quiver ( x , y ) VÏ mòi tªn cho mçi cÆp cña hÖ to¹ ®é cho bëi xij vμ yij
cïng biÕn sè vμ ®é lín lμ dxi vμ dyi.
quiver
( x , y , dx , dy )
VÏ 1 mòi tªn víi täa ®é xi yi cïng biÕn sè vμ ®é lín lμ
tËp dxij vμ dyij.
quiver VÏ mòi tªn nh− trªn nh−ng hÖ sè tû lÖ ®−îc cho bëi gi¸
2
4
6
30
210
60
240
90
270
120
300
150
330
180 0
-5 0 5
-4
-3
-2
-1
0
1
2
3
4
Ch−¬ng 4 - §å ho¹ hai chiÒu
PhÇn 1 - C¬ së 70
( x, y , ... , s ) trÞ s.
NÕu s kh«ng ®−îc khai b¸o th× gi¸ trÞ mÆc ®Þnh lμ 1
quiver
( x, y, ... , str )
VÏ 1 mòi tªn víi kiÓu mÉu ®−êng ®−îc x¸c ®Þnh th«ng
qua biÕn str
feather ( z )
VÏ mòi tªn chØ ra phÇn thùc vμ ¶o cña c¸c phÇn tö hay
ma trËn cña c¸c sè ¶o z.
feather ( x, y ) T−¬ng tù víi feather(x+y*i)
feather ( z, str ) VÏ mòi tªn víi viÖc sö dông kiÓu ®−êng th¼ng str
compass ( z ) VÏ mòi tªn khëi t¹o tõ gèc chØ ra phÇn thùc vμ ¶o cña
c¸c phÇn tö trong ma trËn sè ¶o z
compass ( x, y ) T−¬ng ®−¬ng hμm compass (x + y*i)
compass (z, str) VÏ mòi tªn sö dông kiÓu ®−êng vμ mÉu s¾c ®−îc ®Þnh
nghÜa bëi str
rose ( v ) VÏ biÓu ®å ®èi víi biÓu ®å trßn cho phÐp thÓ hiÖn tÇn
suÊt cña ®èi sè trong vector v.
rose ( u ) T−¬ng tù nh−ng víi kho¶ng x¸c ®Þnh u
rose ( x ) VÏ biÓu ®å ®èi sè víi x lμ vector cña c¸c kho¶ng x¸c
®Þnh.
VÝ dô: Ma trËn z ®−îc x¸c ®Þnh nh− sau:
%
1331
5534
5321
−−−−
−+−
−−+
=
ii
iii
iii
z
clf;
z = [ (1 + i) (2 - i) (3 - 5*i)
(-4 + 3*i) (5 -5*i) (i)
(-1 - i) (3 - 3*i) (-1) ]
subplot(2,2,1); quiver(real(z), imag(z));
title('hμm quiver’);
subplot(2,2,2);feather(z);
title('hμm feather’);
subplot(2,2,3); compass(z);
Ch−¬ng 4 - §å ho¹ hai chiÒu
PhÇn 1 - C¬ së 71
title('hμm compass’);
subplot(2,2,4); rose(angle(z(:)));
title ( 'ham rose ‘);
H
H×
×n
nh
h
4
4.
.1
18
8
§
§å
å
h
ho
o¹
¹
t
th
hu
u
®
®−
−î
îc
c
t
tõ
õ
c
c¸
¸c
c
h
hμ
μm
m
Q
Qu
ui
iv
ve
er
r,
,
T
Te
ea
at
th
he
er
r,
,
C
Co
om
mp
pa
as
ss
s,
,
R
Ro
os
se
e.
.
4
4.
.3
3.
.4
4.
.
L
LÖ
Ön
nh
h
k
ki
iÓ
Óm
m
s
so
o¸
¸t
t.
.
figure ( gef ) HiÓn thÞ cöa sæ graphics hiÖn hμnh. LÖnh figure còng cã thÓ
dïng ®Ó kÝch ho¹t cöa sæ graphic hay t¹o ra mét cöa sæ ®å ho¹
míi.
clf LÖnh dïng ®Ó xo¸ cöa sæ ®å ho¹ hiÖn thêi. ViÖc xo¸ vÉn
thùc hiÖn kÓ c¶ khi chóng ta ®· dïng lÖnh hold on
clg LÖnh xo¸ t−¬ng tù nh− elf vμ cã thÓ kh«ng tån t¹i ë c¸c
version míi cña Matlab.
clc LÖnh xo¸ mμn h×nh lÖnh
home ChuyÓn con trá ®Õn vÞ trÝ 'home' lμ vÞ trÝ ë trªn bªn tr¸i mμn
h×nh.
hold on Gi÷ l¹i tÊt c¶ mμn h×nh ®· vÏ. C¸c lÖnh sau sÏ thªm vμo
mμn h×nh ®å ho¹ chø kh«ng xo¸ mμn h×nh cò ®i.
0 2 4
0
2
4
hµm quiver
0 5 10
-2
0
2
hµm feather
0
-5
0
hµm compass ham rose
1
2
30
210
60
240
90
270
120
300
150
330
180 0