
PH N I: ĐT V N ĐẦ Ặ Ấ Ề
tr ng Ph thông, d y toán là d y ho t đng Toán h c. Đi v i h cỞ ườ ổ ạ ạ ạ ộ ọ ố ớ ọ
sinh, có th coi vi c gi i toán là ho t đng ch y u c a ho t đng toán h c.ể ệ ả ạ ộ ủ ế ủ ạ ộ ọ
Các bài toán tr ng ph thông là m t ph ng ti n r t hi u qu và khôngở ườ ổ ộ ươ ệ ấ ệ ả
th thay th đc trong vi c giúp h c sinh n m v ng tri th c, phát tri n tể ế ượ ệ ọ ắ ữ ứ ể ư
duy, hình thành k năng, k s o ng d ng toán h c vào th c ti n. Ho t đngỹ ỹ ả ứ ụ ọ ự ễ ạ ộ
gi i bài t p toán là đi u ki n đ th c hi n t t các m c đích d y h c toán ả ậ ề ệ ể ự ệ ố ụ ạ ọ ở
tr ng ph thông. Vì v y, t ch c có hi u qu gi i bài t p toán h c có vai tròườ ổ ậ ổ ứ ệ ả ả ậ ọ
quy t đnh đi v i ch t l ng d y h c toánế ị ố ớ ấ ượ ạ ọ .
H ph ng trình là m t d ng toán khá ph bi n trong các đ thi tuy nệ ươ ộ ạ ổ ế ề ể
sinh ĐH, CĐ và đ thi HSG các c p. Đi v i nhi u h c sinh, bài toán gi i hề ấ ố ớ ề ọ ả ệ
ph ng trình đc coi là bài toán khó, th m chí là câu khó nh t trong c u trúcươ ượ ậ ấ ấ
đ thi ĐH, CĐ, thi THPT Qu c gia.ề ố
Qua quá trình gi ng d y h c sinh ôn thi ĐH, CĐ và b i d ng h c sinhả ạ ọ ồ ưỡ ọ
gi i ph i tr c ti p h ng d n h c sinh gi i các h ph ng trình này, tôi th yỏ ả ự ế ướ ẫ ọ ả ệ ươ ấ
c n ph i rèn cho h c sinh thành th o các kĩ năng gi i h ph ng trình thôngầ ả ọ ạ ả ệ ươ
th ng và chú ý t i m t s kĩ năng th ng áp d ng khi gi i “ườ ớ ộ ố ườ ụ ả h không m uệ ẫ
m cự”. Trong bài vi t này tôi xin g i nh v y đi v i các h ph ng trình màế ọ ư ậ ố ớ ệ ươ
thu t gi i không đc trình bày trong sách giáo khoa. ậ ả ượ
Bài vi t đc chia làm ba m c: M đu là tóm t t các h ph ng trìnhế ượ ụ ở ầ ắ ệ ươ
th ng g p, đã đc gi i thi u khá chi ti t trong sách giác khoa. M c th haiườ ặ ượ ớ ệ ế ụ ứ
là m t s kĩ năng gi i h ph ng trình không m u m c. Các bài toán đa raộ ố ả ệ ươ ẫ ự ư
ph n l n là tôi s u t m t nhi u ngu n tài li u khác nhau, trong các kì thi KS,ầ ớ ư ầ ừ ề ồ ệ
thi HSG,…L i gi i các bài toán này tôi chú ý đn cách đa h không m uờ ả ế ư ệ ẫ
m c v d ng quen thu c. Cu i cùng là h th ng các bài t p đ b n đc thamự ề ạ ộ ố ệ ố ậ ể ạ ọ
kh o.ả
Chuyên đ dùng gi ng d y ôn thi ĐH, CĐ và ôn thi HSG cho h cề ả ạ ọ
sinh kh i 12. Th i gian gi ng d y chuyên đ này cho h c sinh kh i 12 khiố ờ ả ạ ề ọ ố
ôn thi ĐH, CĐ là 3 bu i.ổ
M c dù r t tâm huy t v i chuyên đ, nh ng do th i gian và kh năngặ ấ ế ớ ề ư ờ ả
có h n nên bài vi t khó tránh kh i nh ng thi u sót. T i r t mong nh n đcạ ế ỏ ữ ế ố ấ ậ ượ
s góp ý c a quí th y cô, b n bè đng nghi p và các em h c sinh đ chuyênự ủ ầ ạ ồ ệ ọ ể
đ đc hoàn thi n h n và tr thành tài li u có ích trong gi ng d y và h cề ượ ệ ơ ở ệ ả ạ ọ
t p.ậ
1

PH N II: Ầ
M T S PH NG PHÁP GI I H PH NG TRÌNH Ộ Ố ƯƠ Ả Ệ ƯƠ
KHÔNG M U M CẪ Ự
I. M T S H PH NG TRÌNH TH NG G P.Ộ Ố Ệ ƯƠ ƯỜ Ặ
M t s h ph ng trình đc h c trong ch ng trình ph thông cóộ ố ệ ươ ượ ọ ươ ổ
ph ng pháp gi i rõ ràng, h c sinh ch c n nh thu t gi i, rèn luy n các kĩươ ả ọ ỉ ầ ớ ậ ả ệ
năng bi n đi, tính toán là có th làm đc. Th c ch t các h ph ng trìnhế ổ ể ượ ự ấ ệ ươ
này ta g p r t nhi u c THCS và THPT, không riêng b môn toán mà cặ ấ ề ở ả ộ ả
môn lí, môn hóa,… M t l n n a ta nh c l i các d ng h ph ng trình nhộ ầ ữ ắ ạ ạ ệ ươ ư
v y.ậ
1. H hai ph ng trình b c nh t hai n.ệ ươ ậ ấ ẩ
a) Đnh nghĩa: Là h ph ng trình có d ng ị ệ ươ ạ
' ' '
ax by c
a x b y c
+ =
+ =
, trong đó x, y là
n.ẩ
b) Cách gi i: V i h này ta có th gi i b ng nhi u cách khác nhau nh :ả ớ ệ ể ả ằ ề ư
Ph ng pháp th , ph ng pháp c ng, s d ng đ th , s d ng máy tính c mươ ế ươ ộ ử ụ ồ ị ử ụ ầ
tay, tính đnh th c, đt n ph ,…ị ứ ặ ẩ ụ
2. H ba ph ng trình b c nh t ba n.ệ ươ ậ ấ ẩ
a) Đnh nghĩa: Là h ph ng trình có d ng ị ệ ươ ạ
1 1 1 1
2 2 2 2
3 3 3 3
a x b y c z d
a x b y c z d
a x b y c z d
+ + =
+ + =
+ + =
, trong
đó x, y, z là n.ẩ
b) Cách gi i: V i h này ta có th gi i b ng nhi u cách khác nhau nh :ả ớ ệ ể ả ằ ề ư
Ph ng pháp th , ph ng pháp c ng, s d ng máy tính c m tay, tính đnhươ ế ươ ộ ử ụ ầ ị
th c, ph ng pháp kh Gauss,…ứ ươ ử
3. H g m m t ph ng trình b c nh t và m t ph ng trình khác.ệ ồ ộ ươ ậ ấ ộ ươ
a) Đnh nghĩa: Là h ph ng trình có d ng ị ệ ươ ạ
0
( , ) 0
ax by c
f x y
+ + =
=
, trong đó x,
y là n còn ẩf(x,y) là bi u th c hai bi n ể ứ ế x, y.
b) Cách gi i: S d ng ph ng pháp th .ả ử ụ ươ ế
4. H đi x ng lo i 1.ệ ố ứ ạ
2

a) Đnh nghĩa: Là h mà khi ta đi vai trò c a hai n cho nhau trong m iị ệ ổ ủ ẩ ỗ
ph ng trình, t ng ph ng trình đó không thay đi.ươ ừ ươ ổ
b) Cách gi i: Bi n đi t ng đng làm xu t hi n t ng và tích c a cácả ế ổ ươ ươ ấ ệ ổ ủ
nghi m r i đt t ng b ng S, tích b ng P (ệ ồ ặ ổ ằ ằ
24S P
). Thông th ng sau b cườ ướ
này ta đc m t h đn gi n.ượ ộ ệ ơ ả
5. H đi x ng lo i 2.ệ ố ứ ạ
a) Đnh nghĩa: Là h mà khi ta đi vai trò c a hai n cho nhau trong m iị ệ ổ ủ ẩ ỗ
ph ng trình, ph ng trình này bi n thành ph ng trình kia.ươ ươ ế ươ
b) Cách gi i: Tr v cho v làm xu t hi n nhân t chung ả ừ ế ế ấ ệ ử x-y r i đa hồ ư ệ
đã cho v hai h m i đn gi n h n.ề ệ ớ ơ ả ơ
6. H đng c p.ệ ẳ ấ
a) Đnh nghĩa: Là h có d ng ị ệ ạ
1 2
1 2
( ; ) ( ; )
( ; ) ( ; )
f x y f x y
g x y g x y
=
=
, đóở
( ; ) & ( ; )
i i
f x y g x y
là các đa th c đng c p hai bi n và cùng b c.ứ ẳ ấ ế ậ
b) Cách gi i: Xét riêng ảx=0. N u ếx khác 0 thì ta đt ặy=kx r i nh n xét vàồ ậ
chia v cho v ta đc ph ng trình m t n ề ế ượ ươ ộ ẩ k. Tìm đc ượ k ta tìm đc ượ x và y.
II. M T S PH NG PHÁP GI I H PH NG TRÌNHỘ Ố ƯƠ Ả Ệ ƯƠ
KHÔNG M U M C.Ẫ Ự
1. Ph ng pháp bi n đi t ng đngươ ế ổ ươ ươ
M t s kĩ năng th ng áp d ng nh phân tích thành tích, bình ph ngộ ố ườ ụ ư ươ
ho c l p ph ng hai v , thêm b t làm xu t hi n nhân t chung,…ặ ậ ươ ế ớ ấ ệ ử
Bài 1. Gi i h ph ng trình: ả ệ ươ
2 2
2 2 2 (1)
1 2. (2)
x xy y y x
y x y x
+ + = +
− + + =
Gi i:ả Cách 1: Nh n th y, n u coi ph ng trình (1) là ph ng trình b cậ ấ ế ươ ươ ậ
hai n x còn y là tham s , ta có ph ng trình (1) ẩ ố ươ
2 2
( 2) 2 2 0x x y y y+ − + − =
( )
( )
22
2 4 2 2y y y∆ = − − −
=
( )
2
3 2y−
(3)
(1) 2 2 (4)
x y
x y
=
= −
T (3) & (2) ta có ừx=y=1. T (4) & (2) ta có ừ
0; 2
2 2
1 8
; .
3 3 2 3 3
y x
x y
y x
y y y
= =
= −
= − =
− =
3

K t lu n: H có 3 nghi m (1; 1); (2; 0);ế ậ ệ ệ
8 1
( ; )
3 3
−
Cách 2: ĐK:
1 0.x y− +
Ta bi n đi ph ng trình (1) làm xu t hi nế ổ ươ ấ ệ
nhân t chung ử
2 2 2
(3)
(1) 2 2 0 ( )( 2 2) 0 2 2 (4)
x y
x y xy y y x x y x y x y
=
− + − + − = − + − =� � � = −
T (3) & (2) ta có ừx=y=1. T (4) & (2) ta có ừ
0; 2
2 2
1 8
; .
3 3 2 3 3
y x
x y
y x
y y y
= =
= −
= − =
− =
K t lu n: H có 3 nghi m (1; 1); (2; 0);ế ậ ệ ệ
8 1
( ; )
3 3
−
Bài 2. (Báo TH&TT) Gi i h ph ng trình: ả ệ ươ
2 2
2
21 (1)
(2)
xy
x y x y
x y x y
+ + =
+
+ = −
Gi i:ả ĐK:
0.x y+ >
Ta có
2 2 2
2 2
2 1
(1) 2 2 1 ( ) 1 2 . 0
1 (3)
2
( 1) 1 0 0 (4)
xy x y
x xy y xy x y xy
x y x y
x y
xy
x y x y x y x y
x y x y
+ −
+ + + − = + − − =� �
+ +
= −
� �
+ − + + − =� � + + +
� �
+=
� � +
- T (3) và (2) ta có ừ
20; 1
3 0 3; 2
y x
y y y x
= =
− = = = −
.
- Vì
0x y+ >
nên (4) không th a mãn. ỏV y h có hai nghi m.ậ ệ ệ
Bài 3. (Đ thi TS cũ)ề Gi i h ph ng trình: ả ệ ươ
3 3 3
2 2
1 19 (1)
6 (2)
x y x
y xy x
+ =
+ = −
Gi i:ả N u ếx=0, (1) tr thành 1=0, vô lí. V y ở ậ x khác 0. Nhân hai v c aế ủ
(1) v i 6, hai v c a (2) v i 19ớ ế ủ ớ x ta đc: ượ
3 3 3
2 2 3
6 6 114
19 19 114
x y x
xy x y x
+ =
+ = −
C ng v v i v ta đc: ộ ế ớ ế ượ
3 3 2 2
6 19 19 6 0x y x y xy+ + + =
, gi i ph ng trình b cả ươ ậ
ba này ta đc ượ
2 3
; ; 1.
3 2
xy xy xy= − = − = −
- N u ế
2
3
xy = −
thì
3
8 1
(1) 1 19 2.
27 3
x x y− = = = −� � �
- N u ế
3
3 27 1
,(1) 1 19 3
2 8 2
xy x x y= − − = = − =� � �
- N u ế
1,(1) 0,xy x= − =�
vô lí.
4
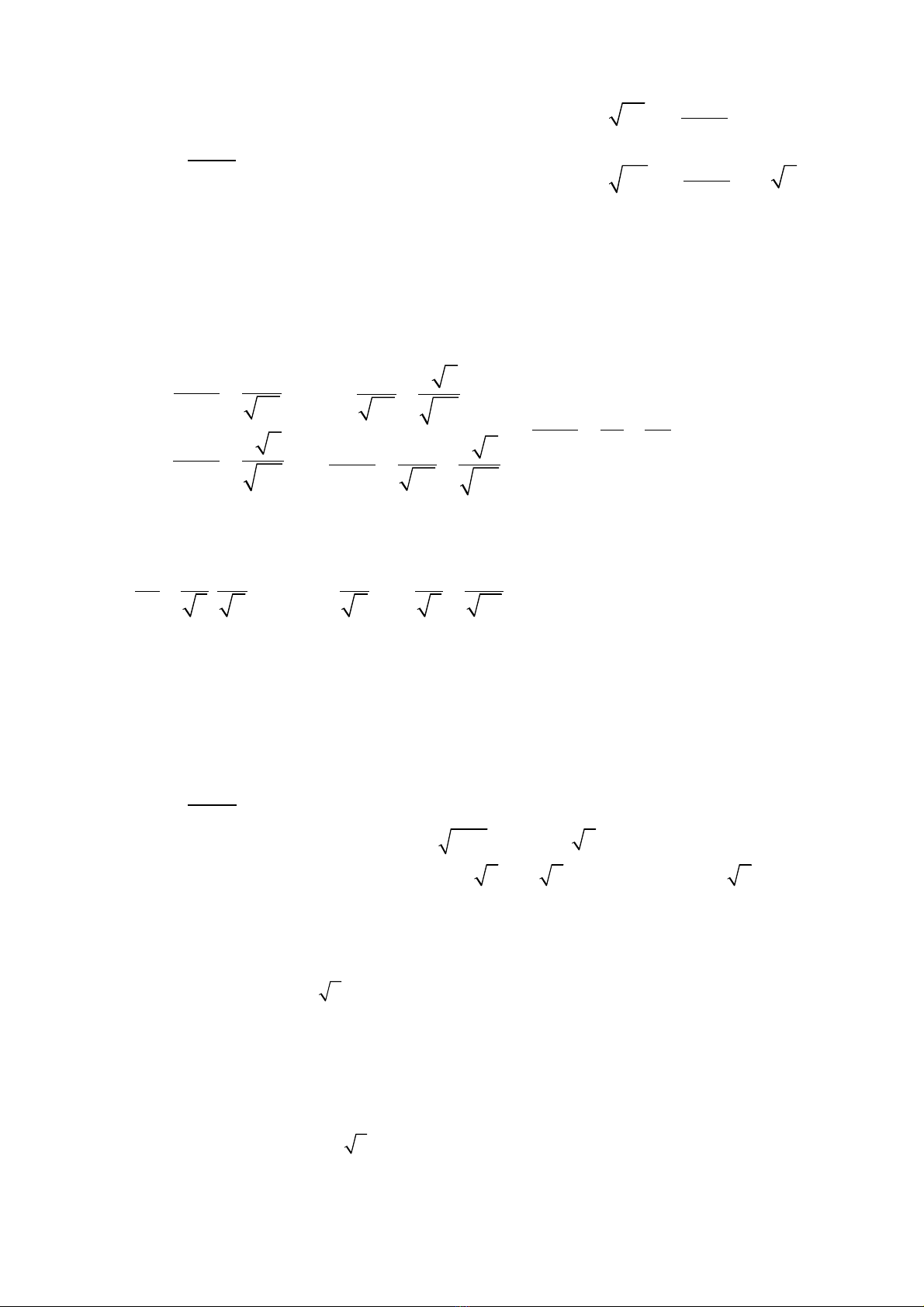
Bài 4. (HSG QG 1996) Gi i h ph ng trình:ả ệ ươ
1
3 (1 ) 2 (1)
1
7 (1 ) 4 2 (2)
xx y
yx y
+ =
+
− =
+
Gi i: ả
ĐK
0 & 0.x y
D th y ễ ấ x=0 ho c ặy=0 không th a mãn h . ỏ ệ
V i x>0, y>0 ta có ớ
1 2 1 2 2
11
33 7 1 1 8
3 7
1 4 2 1 1 2 2
173 7
x y xx y
x y x y
x y yx y x y
+ = = +
+
� � = −� �
� � +
� �
− = = −
� �
++
(nhân v v i v )ế ớ ế
2 2
21 (7 24 )( ) 24 38 7 0 6xy y x x y x xy y y x= − + + − = =� � �
(vì x, y d ng).ươ
Thay vào ph ng trình (1) ta đcươ ượ
1 2 1 1 1 2
. 1 0 7 .
73 3 21
xx x
� �
− + = =� �
� �
� �
T đó suy ra ừx và y.
2. Ph ng pháp đt n ph .ươ ặ ẩ ụ
M t s ph ng trình sau khi nhân ho c chia hai v cho cùng m t bi uộ ố ươ ặ ế ộ ể
th c khác không ho c b ng m t s đng tác tách và ghép khéo léo ta làm xu tứ ặ ằ ộ ố ộ ấ
hi n các đi l ng mà nh cách đt n ph ta có th đa h ph c t p vệ ạ ượ ờ ặ ẩ ụ ể ư ệ ứ ạ ề
m t h đn gi n, quen thu c.ộ ệ ơ ả ộ
Bài 5. (Thi KSCL môn thi THPT QG c a THPT Lê L i năm h c 2014-2015)ủ ợ ọ
Gi i h ph ng trình:ả ệ ươ
3
2 2 2
4 4 4
1 8
( ) ( 1) 2( 1) ( 3) 1
y y x
y x x y y x
− + = +
− + + = − − − −
Gi i:ả Đi u ki n: ề ệ
( )
1*
0
y
x
T pt (1), đt t = ừ ặ
4
x
ta có pt
2
2
(1 ) 2 ( 1) 0 1
y t
y t y t t y t
= −
− − − + = = +
V i ớ
2y t= −
k t h p v i đk (*) suy ra vô nghi m.ế ợ ớ ệ
V i ớ
4
4
1 1 ( 1)y t y x x y= + = + = −� �
Thay vào (1) ta có
5




![Bài tập so sánh hơn và so sánh nhất của tính từ [kèm đáp án/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250808/nhatlinhluong27@gmail.com/135x160/77671754900604.jpg)
![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)




![Tài liệu Lý thuyết và Bài tập Tiếng Anh lớp 6 [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250802/hoihoangdang@gmail.com/135x160/18041754292798.jpg)





