Assoc. Prof. NguyÔn V¨n NhËn - Engineering Thermodynamics - 2007
Chương 1
KHÁI NIỆM CƠ BẢN
1.1. HỆ NHIỆT ĐỘNG
1.1.1. ĐỊNH NGHĨA
Hệ nhiệt động (HNĐ) là một vật hoặc nhiều vật được tách riêng ra khỏi các vật
khác để nghiên cứu những tính chất nhiệt động của chúng. Tất cả những vật ngoài
HNĐ được gọi là môi trường xung quanh (MTXQ). Vật thực hoặc tưởng tượng ngăn
cách hệ nhiệt động và MTXQ được gọi là ranh giới của HNĐ.
1.1.2. PHÂN LOẠI
Rigid
vessel
System
boundaries
Water
vapor
Liquid
water
Cylinder
System
boundaries
Piston
Pump
Electrical power in
a)b)
c)
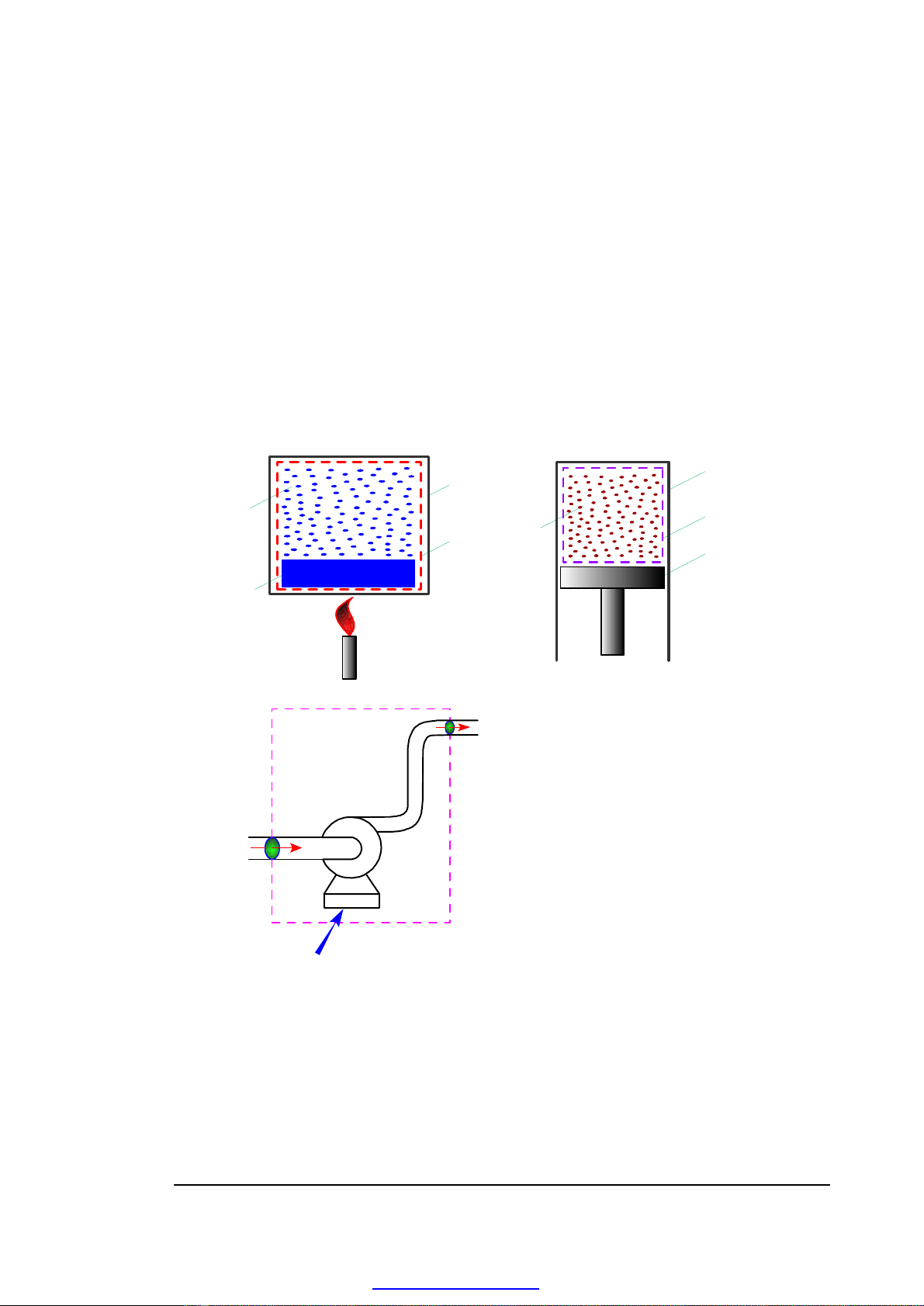
Fig. 1.1 - Thermodynamic Systems
a) Closed system with constant
volume, b) Closed system with
nonconstant volume, c) Open system
• Hệ nhiệt động kín - HNĐ trong đó không có sự trao đổi vật chất giữa hệ
và MTXQ.
• Hệ nhiệt động hở - HNĐ trong đó có sự trao đổi vật chất giữa hệ và
MTXQ.
• Hệ nhiệt động cô lập - HNĐ được cách ly hoàn toàn với MTXQ.
PDF created with pdfFactory trial version www.pdffactory.com
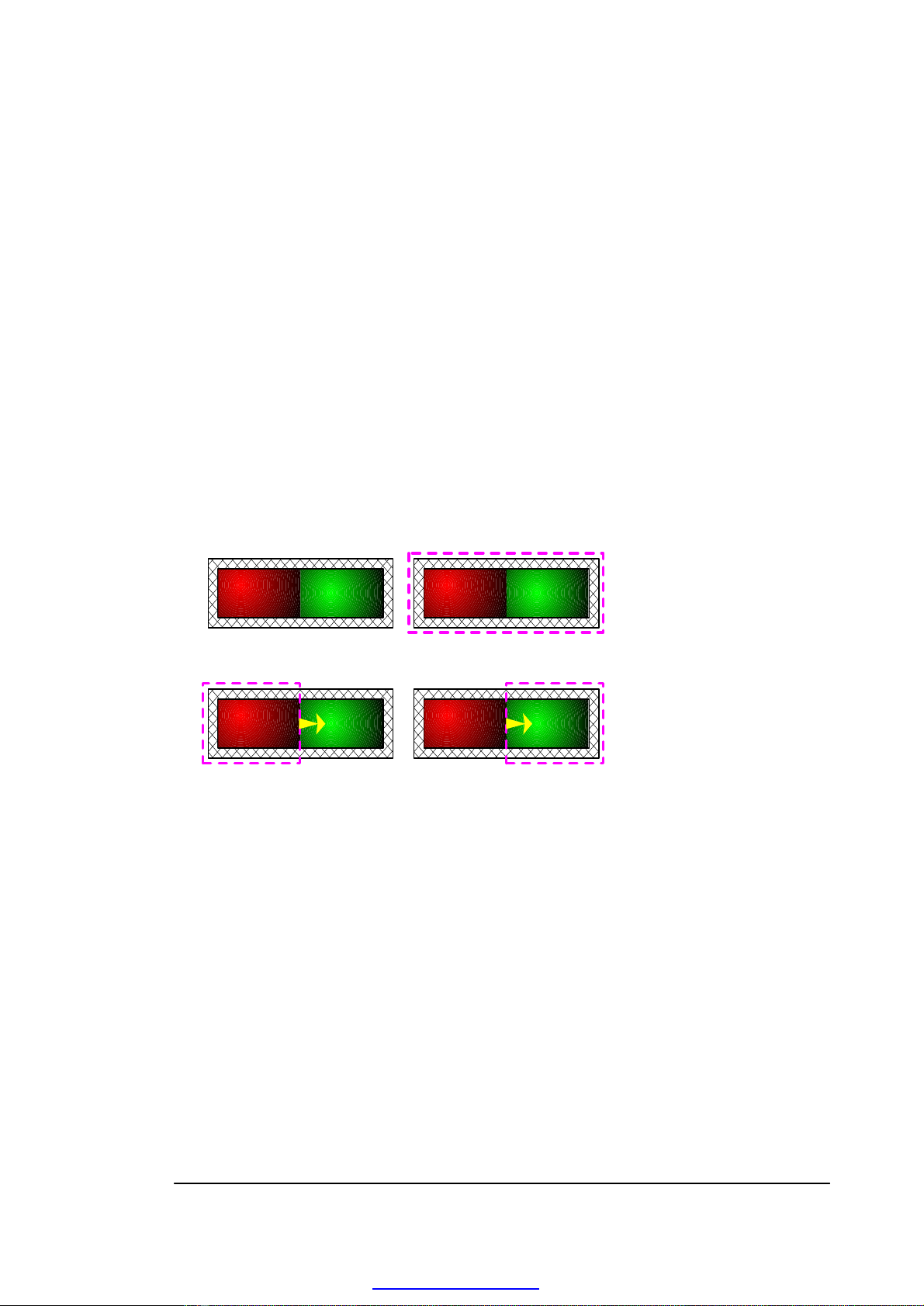
- 4 -
Assoc. Prof. Nguyễn Văn Nhận - Engineering Thermodynamics - 2007
1.1.3. LỰA CHỌN RANH GIỚI HỆ NHIỆT ĐỘNG
In working examples, one must first choose the boundaries of the system to be
analyzed. Sometimes the choice will be quite obvious, but at other times it must be
carefully chosen to provide the desired answer. The importance of the choice of
system boundaries can be seen from the following example.
Consider the case of two bricks, one hot and other cold, that are placed so that
two sides are in contact. Insulation material is wrapped around both bricks, as shown
in Fig. 1-2a.
First choose the system to include both bricks and insulation (Fig. 1-2b).
Because of the insulation, no heat crosses the boundaries of the system.
Next choose the system to include the hot brick and part of the insulation (Fig.
1-2c). In this case, heat is transferred across the system boundary out of the system.
Finally, choose the system to include the cold brick and the insulation (Fig. 1-
2d). In this case, heat crosses the system boundary and is transferred into the system
a)b)
c)d)
Fig. 1-2. Choice of
System Boundary
Q
out
Q
in
PDF created with pdfFactory trial version www.pdffactory.com
- 5 -
Assoc. Prof. Nguyễn Văn Nhận - Engineering Thermodynamics - 2007
1.2. CÁC THÔNG SỐ TRẠNG THÁI CỦA MCCT
Môi chất công tác (MCCT) - chất có vai trò trung gian trong quá trình biến đổi
năng lượng.
Thông số trạng thái của MCCT - đại lượng vật lý đặc trưng cho trạng thái nhiệt
động của MCCT.
1.2.1. NHIỆT ĐỘ
Khái niệm
Nhiệt độ (T) - số đo trạng thái nhiệt của vật. Theo thuyết động học phân tử,
nhiệt độ là số đo động năng trung bình của các phân tử .
2
.
3
m
kT
µ
ω⋅
=
(1.1)
trong đó : mµ - khối lượng phân tử ; ω - vận tốc trung bình của các phân tử ; k -
hằng số Bonzman , k = 1,3805 . 105 J/deg ; T - nhiệt độ tuyệt đối..
Nhiệt kế
Nhiệt kế hoạt động dựa trên sự thay đổi một số tính chất vật lý của vật thay đổi
theo nhiệt độ, ví dụ : chiều dài, thể tích, màu sắc, điện trở , v.v.
0
40
80
120
Fig. 1-3. Thermometer
Thang nhiệt độ
• Thang nhiệt độ (0C) - (Anders Celsius - 1701 - 1744 - Sweden scientist)
• Thang nhiệt độ Fahrenheit Scale (0F) - (Daniel Fahrenheit - 1686 -
1736 - Gdansk inhabitant) .
• Thang nhiệt độ Kelvin (K) - (Kelvin - 1824 - 1907 - English Physicist ).
• Thang nhiệt độ Rankine (0R)
)32(
9
5
00 −=FC ; 273
0−= KC
32
5
9
00 +⋅=CF ; 273
0+= CK
KR
5
9
0
= ; RK
0
9
5
=
0
R = 0 F + 459,67
PDF created with pdfFactory trial version www.pdffactory.com
- 6 -
Assoc. Prof. Nguyễn Văn Nhận - Engineering Thermodynamics - 2007
1.2.2. ÁP SUẤT
Khái niệm
Áp suất của lưu chất (p) - lực tác dụng của các phân tử theo phương pháp tuyến
lên một đơn vị diện tích thành chứa.
A
F
p=
(1.2a)
Theo thuyết động học phân tử :
2
3
m
pn
µ
α
⋅
=⋅⋅ (1.2b)
trong đó : p - áp suất ; F - lực tác dụng của các phân tử ; A - diện tích thành bình chứa
; n - số phân tử trong một đơn vị thể tích ; α - hệ số phụ thuộc vào kích thước và lực
tương tác của các phân tử.
Đơn vị áp suất
1) N/m2 ; 5) mm Hg (tor - Torricelli, 1068-1647)
2) Pa (Pascal) ; 6) mm H2O
3) at (Technical Atmosphere) ; 7) psi (Pound per Square Inch)
4) atm (Physical Atmosphere) ; 8) psf (Pound per Square Foot)
at Pa mm H2O mm Hg (at 0 0C)
1 at 1 9,80665.10 4 1.10 4 735,559
1 Pa 1,01972.10 -5 1 0,101972 7,50062.10 -3
1 mm H2O 1.10 -4 9,80665 1 73,5559.10 -3
1 mm Hg 1,35951.10 -3 133,322 13,5951 1
1 atm = 760 mm Hg (at 0 0C) = 10,13 . 10 4 Pa = 2116 psf (lbf/ft2)
1 at = 2049 psf
1 psi (lbf/in2) = 144 psf = 6894,8 Pa
1lbf/ft2 (psf) = 47,88 Pa
Phân loại áp suất
• Áp suất khí quyển (p0) -
• Áp suất dư (pd) - áp suất của lưu chất so với môi trường xung quanh
p
d = p - p 0
• Áp suất tuyệt đối (p) - áp suất của lưu chất so với chân không tuyệt đối.
p = p d + p 0
• Độ chân không (pck) - phần áp suất nhỏ hơn áp suất khí quyển.
p
ck = p0 - p
PDF created with pdfFactory trial version www.pdffactory.com
- 7 -
Assoc. Prof. Nguyễn Văn Nhận - Engineering Thermodynamics - 2007
p
p0
pd
p
p0
pck
Fig. 1-4. Pressures
Áp kế
p
p
d
p
0
p0
Hg
Vacuum
a)b)
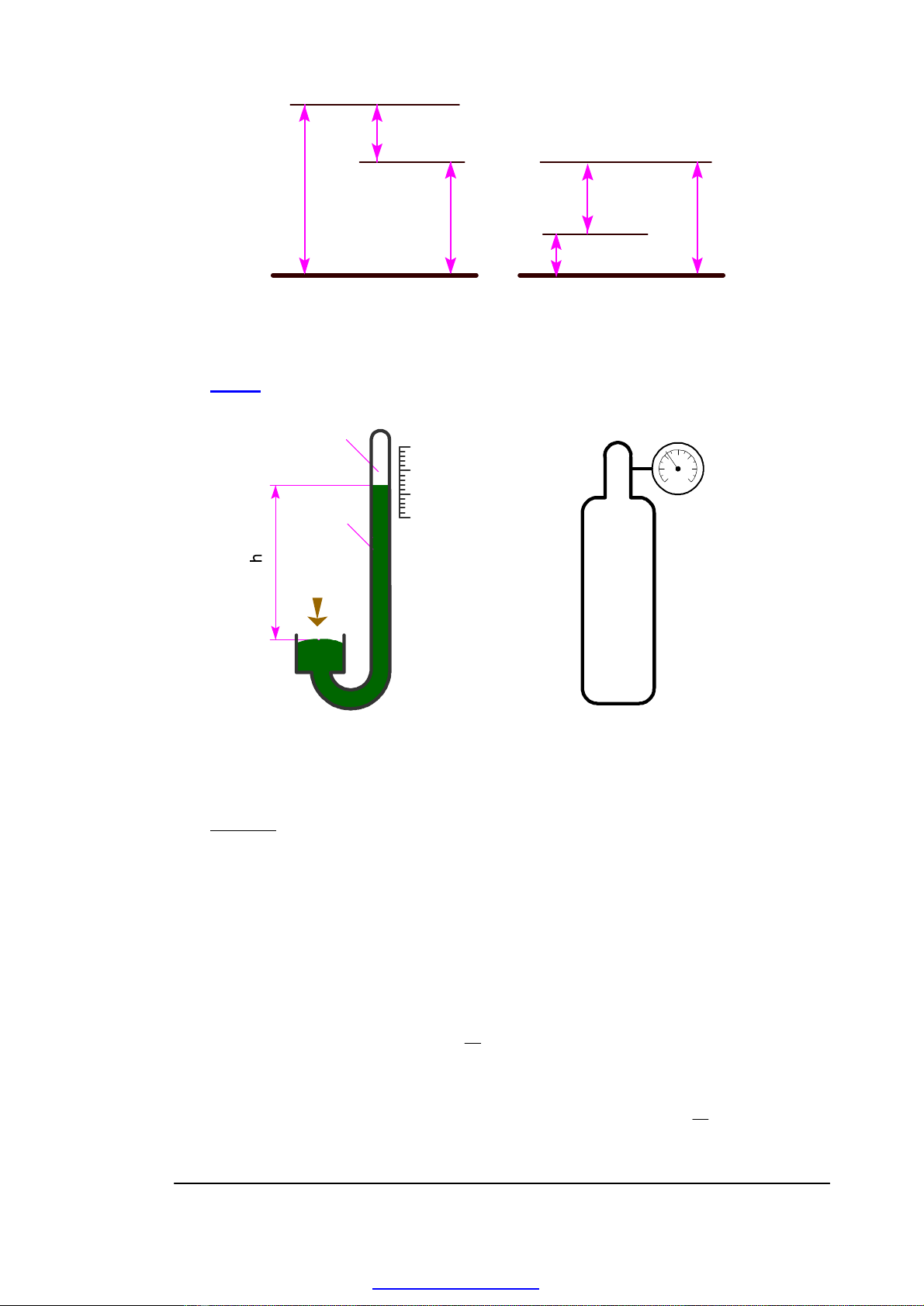
Fig. 1-5. Methods used to measure the pressure
a) Barometer , b) Pressure gause
Ghi chú : Khi đo áp suất bằng áp kế thủy ngân, chiều cao cột thủy ngân cần
được hiệu chỉnh về nhiệt độ 0 0C.
h
0
= h (1 - 0,000172. t) (1.3)
trong đó : t - nhiệt độ cột thủy ngân, [0C] ; h0 - chiều cao cột thủy ngân hiệu chỉnh
về nhiệt độ 0 0C ; h - chiều cao cột thủy ngân ở nhiệt độ t 0C.
1.2.3. THỂ TÍCH RIÊNG VÀ KHỐI LƯỢNG RIÊNG
• Thể tích riêng (v) - Thể tích riêng của một chất là thể tích ứng với một
đơn vị khối lượng chất đó :
m
V
v= [m3/kg]
•
Khối lượng riêng (ρ) - Khối lượng riêng - còn gọi là mật độ - của một chất
là khối lượng ứng với một đơn vị thể tích của chất đó :
V
m
=ρ [kg/m3]
PDF created with pdfFactory trial version www.pdffactory.com