Lecture Probability & statistics: Chapter 4 - Bùi Dương Hải

Chia sẻ: Minh Hoa | Ngày: | Loại File: PDF | Số trang:40

Thêm vào BST

Báo xấu

43
lượt xem 1
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Lecture "Probability & statistics - Chapter 4: Basic probability" has contents: Probability, outcome – event complement event, intersection event, union event mutually exclusive, independent, collectively exhausive, partitions bernoulli formula total probability, bayes’ theorem.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Lecture Probability & statistics: Chapter 4 - Bùi Dương Hải

Lecture 4. BASIC PROBABILITY  Probability  Outcome – Event  Complement Event, Intersection Event, Union Event  Mutually Exclusive, Independent, Collectively Exhausive, Partitions  Bernoulli Formula  Total Probability, Bayes’ Theorem  [1] Chapter 4, pp. 169 - 212 PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 1
“Problem of Points”  2 players A and B, contributed 50 Franc each.  The game is winner – loser only (no draw), A and B are equally-likely to win in each match.  Game rule: play 9 matches, the one wins more is final winner and takes all of 100F  But the game had stopped after 7 matches, and scores at that time of A and B are 4 and 3, respectively.  How could they distribute the money? PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 2
4.1. Probability  Probability is quantitative measure of uncertainty, the chance that an uncertain event will occur.  Probability: Subjective and Objective  Probability of event A is denoted by P(A)  0 ≤ P(event) ≤ 1  P(always) = 1  P(impossible) = 0  ( ) > ( ): A is more possible to occur than B PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 3
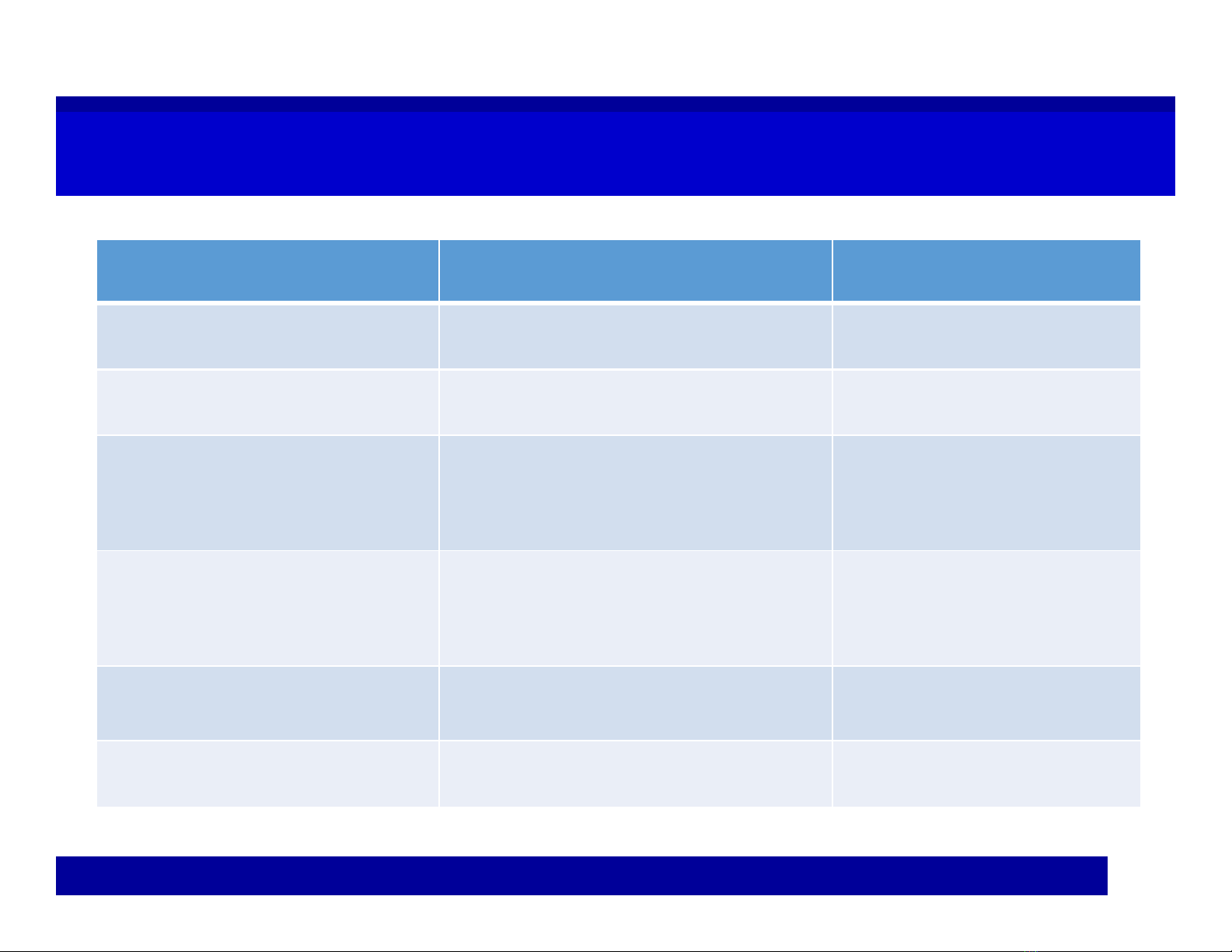
Experiment – Outcome - Event Experiment Outcome Event Flip a coin Head, tail ‘Head’, ‘tail’ Toss a die 1,2,3,4,5,6 dot(s) ‘greater than 3’ Do an exam Score = 0, 1, 2,…, 10 ‘pass’; ‘excellent’ Invest in a project Profit: (+), (–), zero ‘Non negative’ ‘profitable’ Apply for a job Pass, fail Do a job Salary = … PROBABILITY & STATISTICS– Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 4
Classical Probability  Sample space: all basic outcomes, denoted by Ω  Assumes all basic outcomes in the sample space are equally-likely to occur  Number of basic outcomes:  Number of basic outcomes for event A:  Probability of event A: = PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 5
Classical Probability Example 4.1. Flipping a “fair” coin once, the probability that the Head is up = ? Example 4.2. Flipping a fair coin two times. What is the probability of (a) “There are 2 Heads” (b) “There are 1 Head, 1 Tail” (c) “There are 2 Tails” PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 6
Classical Probability Example 4.3: Flip a coin three times, what is the probability of (a) There are 2 Heads only? (b) There are Heads only? (c) There are 2 Heads, given the first is Head? (d) There are 2 Heads, given the first is Tail? Example 4.4 There is a box contains 6 white balls and 4 black balls. Random pick up 2 balls, calculate the probability of event that both balls are white, in 3 cases: (a) Pick up one, replace, then the next (b) Pick up one by one, without replacement (c) Pick up 2 balls simultaneously PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 7
Example  Frequency Table Probability Table Male Female Sum Male Female Sum Freq. 160 240 400 Prob. 0.4 0.6 1  Cross-Frequency Table Joint Probability Table Freq. Male Female Sum Prob. Male Female Sum Single 60 80 140 Single 0.15 0.2 0.35 Married 100 160 260 Married 0.25 0.4 0.65 Sum 160 240 400 Sum 0.4 0.6 1 PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 8
4.2. Probability vs Proportion  Number of experiments:  Frequency of event A:  Proportion of A:  When n is large enough: ( ) ≈ / Ex. In 100,000 new-borns, there were 51,000 boys, then the probability of “new-born is boy” is about 0.51 Ex. In 4,000 students, there are 600 fail in subject A, then probability of “Fail in subject A” is about 0.15 PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 9
4.3. Complement Event  Complement of A : all outcomes that not belong to A  Denoted by Ā A Ā Ω Ex.  A = “two flipped coins are Heads”  A = ?  B = “both picked balls are White”  B = ?  C = “all of students passed”  C = ? PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 10
Law of Complement  Law: ( ) = – ( ) Ex. Flipping coin twice, what is the Probability of “Have at least one Tail” ?  Complement of “Have at least one tail” is “No any Tail”, or “Two Heads”  Probability = 1 – P(Two Heads) = 1 – ¼ = ¾  PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 11
4.4. Intersection Event  Intersection of A and B: all outcomes that belong to both A and B,  Denoted by ∩  ∩ ̅=Ø A AÇB B Ω Ex. Pick 2 balls from the box of Blacks and Whites, A is “The first is white” , B is “The second is white” AÇB is “Both balls are white” PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 12
Mutually Exclusive  A and B are Mutually exclusive : have no common  i.e., A Ç B = Ø  A and Ā ? A B Ω Ex. Pick up 2 balls, A = “two Whites”, B = “two Blacks”, C = “At least one White”  A and B are mutually exclusive; B and C are mutually exclusive, but A and C are NOT mutually exclusive, PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 13
Conditional Probability  Conditional probability : probability of one event, given that another event has occurred.  The conditional probability of B given that A has occurred, (B given A) denoted by P(B | A) Ex. Flip a coin 3 times P(2 Heads) = 3/8 = 0.375 P(2 Heads | The first is Head) = 2/4 = 0.5 P(2 Heads | The first is Tail) = 1/4 = 0.25 P(2 Heads | There are at least one Head) = PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 14
Conditional Probability Ex. Pick up one ball from box of 6 Whites and 4 Blacks, then one more. Let A = “the first ball is White”, B = “The second ball is White”  Without replacement of the first ball: P(B | A) = 5/9  Replacement of the first ball: P(B | A) = 6/10 Ex. Pick up 3 balls one-by-one, without replacement  P(The third is White | Two firsts are Whites) =  P(The third is White | Two firsts are 1 White 1 Black) =  P(The third is White | Two firsts are Blacks) = PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 15
Independent Events  A and B are independent : A does not affect B, and B does not affect A  Û ( | ) = ( ) and ( | ) = ( )  A and B are not independent  dependent Ex. From box of 6 Whites, 4 Blacks, pick up one by one Let A = “the 1st is White”, B = “The 2nd is White”.  Replace the first  A and B are independent ( | ) = ( |Ā) = 6/10 ; ( | ) = 6/10  Without replacement  A and B are dependent ( | ) = 5/9 ; ( |Ā) = 6/9 PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 16
Law of Intersection  ∩ = × = × ( | )  A and B are independent Û ∩ = × ( )  Conditional Probability ∩ = PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 17
Law of Intersection Ex. Pick one ball from box of 6 whites and 4 blacks, then one more. Let A = “the first ball is White”, B = “The second ball is White”.  The Probability of “Two White” = ( Ç ) ( Ç ) = ( )× ( | )  Without replacement Ç = × =  Replacement Ç = × = PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 18
Example Example 4.5. The chance that a student passes the subjects A and B are 0.6 and 0.8, respectively. However, if passed subject A, the chance for him to pass subject B is 0.9 (a) What is probability that he passes both subjects? (b) Whether “Pass subject A” and “Pass subject B” are independent? (c) What is probability of passing subject A, given B has been passed? PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 19
In General  Intersection of n events A1 and A2 and… and An ∩ ∩ ⋯∩  A1, A2,…,An are totally independent Û ( ∩ ∩ ⋯∩ ) = ( )× ⋯× ( ) Ex. Pick 5 balls from box of 6 Whites and 4 Backs, with replacement, the Probability that all of them are white is 6 6 6 6 6 × × × × = 0.6 10 10 10 10 10 PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 20