Khóa học LTĐH KIT-1: Môn Toán – Thầy Lê Bá Trần Phương
Phương trình chứa căn
Hocmai.vn – Ngôi trường chung của học trò Việt
Tổng đài tư vấn: 1900 58-58-12
- Trang | 1 -
Dạng 2: Đặt ẩn phụ (tiếp)
Bài 5: Tìm m để phương trình sau có nghiệm
1. (ĐHKB -2004):
2 2 4 2 2
1 1 2 2 1 1 1m x x x x x
2. (TK- 2011):
6 2 (4 )(2 2) 4 4 2 2x x x m x x
3. (TK- 2010 :
2
9 2 4 2 2x m x x
4. (TK - 2009):
Bài 6: (ĐHKA – 2007) Tìm m để phương trình sau có nghiệm:
2
4
3 1 1 2 1x m x x
Bài 7: Tìm m để phương trình sau có nghiệm
12 5 4x x x m x x
Bài 8: (ĐHKA – 2008): Tìm m để phương trình sau có nghiệm
Bài 9: Giải phương trình
13
1. 12
xx
xx

33
21
2. 2
12
xx
xx

Giáo viên: Lê Bá Trần Phƣơng
Nguồn: Hocmai.vn
BÀI 3. PHƢƠNG TRÌNH CHỨA CĂN (PHẦN 3)
TÀI LIỆU BÀI GIẢNG
Giáo viên: LÊ BÁ TRẦN PHƢƠNG
Đây là tài liệu tóm lược các kiến thức đi kèm với bài giảng Bài 3. Phương trình chứa căn (phần 3) thuộc khóa học
LTĐH KIT-1: Môn Toán – Thầy Lê Bá Trần Phương tại website Hocmai.vn. Để có thể nắm vững kiến thức phần Bài
3. Phương trình chứa căn (phần 3), bạn cần kết hợp xem tài liệu cùng với bài giảng này.
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com
Khóa học LTĐH KIT-1: Môn Toán – Thầy Lê Bá Trần Phương
Phương trình chứa căn
Hocmai.vn – Ngôi trường chung của học trò Việt
Tổng đài tư vấn: 1900 58-58-12
- Trang | 1 -
Bài 1: Tìm m để phương trình sau có nghiệm:
2
9 2 4 2 2x m x x
Bài 2: Tìm m để phương trình:
23
2 2 1 3 2x mx x x
có hai nghiệm thực phân biệt.
Bài 3: Tìm m để phương trình sau có nghiệm:
22
44
1 2 1 1 2 1x x m x x
Bài 4: Tìm m để phương trình sau có nghiệm:
22
3 2 3 ( 1) 1x x m x x
Bài 5 : Tìm m để phương trình sau có nghiệm:
6 2 (4 )(2 2) 4 4 2 2x x x m x x
Giáo viên: Lê Bá Trần Phƣơng
Nguồn: Hocmai.vn
BÀI 3. PHƢƠNG TRÌNH CHỨA CĂN (PHẦN 3)
BÀI TẬP TỰ LUYỆN
Giáo viên: LÊ BÁ TRẦN PHƢƠNG
Các bài tập trong tài liệu này được biên soạn kèm theo bài giảng Bài 3. Phương trình chứa căn (phần 3) thuộc khóa học
LTĐH KIT-1: Môn Toán – Thầy Lê Bá Trần Phương tại website Hocmai.vn giúp các bạn kiểm tra, củng cố lại các
kiến thức được giáo viên truyền đạt trong bài giảng Bài 3. Phương trình chứa căn (phần 3). Để sử dụng hiệu quả, bạn
cần học trước bài giảng sau đó làm đầy đủ các bài tập trong tài liệu này.
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com
Khóa học LTĐH KIT-1: Môn Toán – Thầy Lê Bá Trần Phương
Phương trình chứa căn
Hocmai.vn – Ngôi trường chung của học trò Việt
Tổng đài tư vấn: 1900 58-58-12
- Trang | 1 -
Bài 1: Tìm m để phương trình sau có nghiệm:
2
9 2 4 2 2x m x x
Giải:
Điều kiện:
22x
Đặt
2 2 , 2 2 2t x x t
Chú ý:
2 2 , 2 2t x x x
Ta có:
2
1 1 2 2
'2 2 2 2 24
xx
txx x

' 0 2 2 0t x x x
(0) 2 2; ( 2) 2, (2) 2t t t
min 2; 2 2 2 2 2t Maxt t
22
4 2 4tx
, thay vào phương trình ta có:
2
5 , 2 2 2t mt t
25tm
t

Bài toán trở thành: tìm m để phương trình:
25tm
t
có nghiệm
2 2 2t
Xét hàm
25
( ) , 2 2 2
t
f t t
t
Ta có:
22
2
5
5
'( ) ; '( ) 0 5 0 5
t
t
f t f t t
tt

Bảng biến thiên:
t
-
-
5
0 2
5
22
'f
+ 0 - - 0 +
f
9
2
13 2
4
25
BÀI 3. PHƢƠNG TRÌNH CHỨA CĂN (PHẦN 3)
ĐÁP ÁN BÀI TẬP TỰ LUYỆN
Giáo viên: LÊ BÁ TRẦN PHƢƠNG
Các bài tập trong tài liệu này được biên soạn kèm theo bài giảng Bài 3. Phương trình chứa căn (phần 3) thuộc khóa học
LTĐH KIT-1: Môn Toán – Thầy Lê Bá Trần Phương tại website Hocmai.vn giúp các bạn kiểm tra, củng cố lại các
kiến thức được giáo viên truyền đạt trong bài giảng Bài 3. Phương trình chứa căn (phần 3). Để sử dụng hiệu quả, bạn
cần học trước bài giảng sau đó làm đầy đủ các bài tập trong tài liệu này.
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com
Khóa học LTĐH KIT-1: Môn Toán – Thầy Lê Bá Trần Phương
Phương trình chứa căn
Hocmai.vn – Ngôi trường chung của học trò Việt
Tổng đài tư vấn: 1900 58-58-12
- Trang | 2 -
Phương trình
25tm
t
có nghiệm
2 2 2t
khi và chỉ khi hai đồ thị
25
( ) , 2 2 2
()
t
f t t
t
f t m
cắt nhau.
Từ bảng biến thiên suy ra giá trị cần tìm là:
13
2 5 2
4
m
Bài 2: Tìm m để phương trình:
23
2 2 1 3 2x mx x x
có hai nghiệm thực phân biệt.
Giải:
+ Điều kiện bài toán:
3
2 0 0x x x
+ ta có:
23
2 2 1 3 2 (1)x mx x x
23
2 2 1 3 2mx x x x
Nhận thấy
0x
không phải là nghiệm của (1)
11
(1) 2 2 3 2m x x
xx
+ Đặt
11
2 , ì 0 2 2 2x t v x x
xx
(theo bất đẳng thức côsi)
+ Xét
2
2
1 2 1
( ) 2 ó ' 0
x
y f x x c y
xx
1
2
x
Dựa vào bảng biến thiên ta thấy với mỗi
22t
thì có hai nghiệm
0x
.
(1) trở thành
13 2 2 (2)
22
m t t t
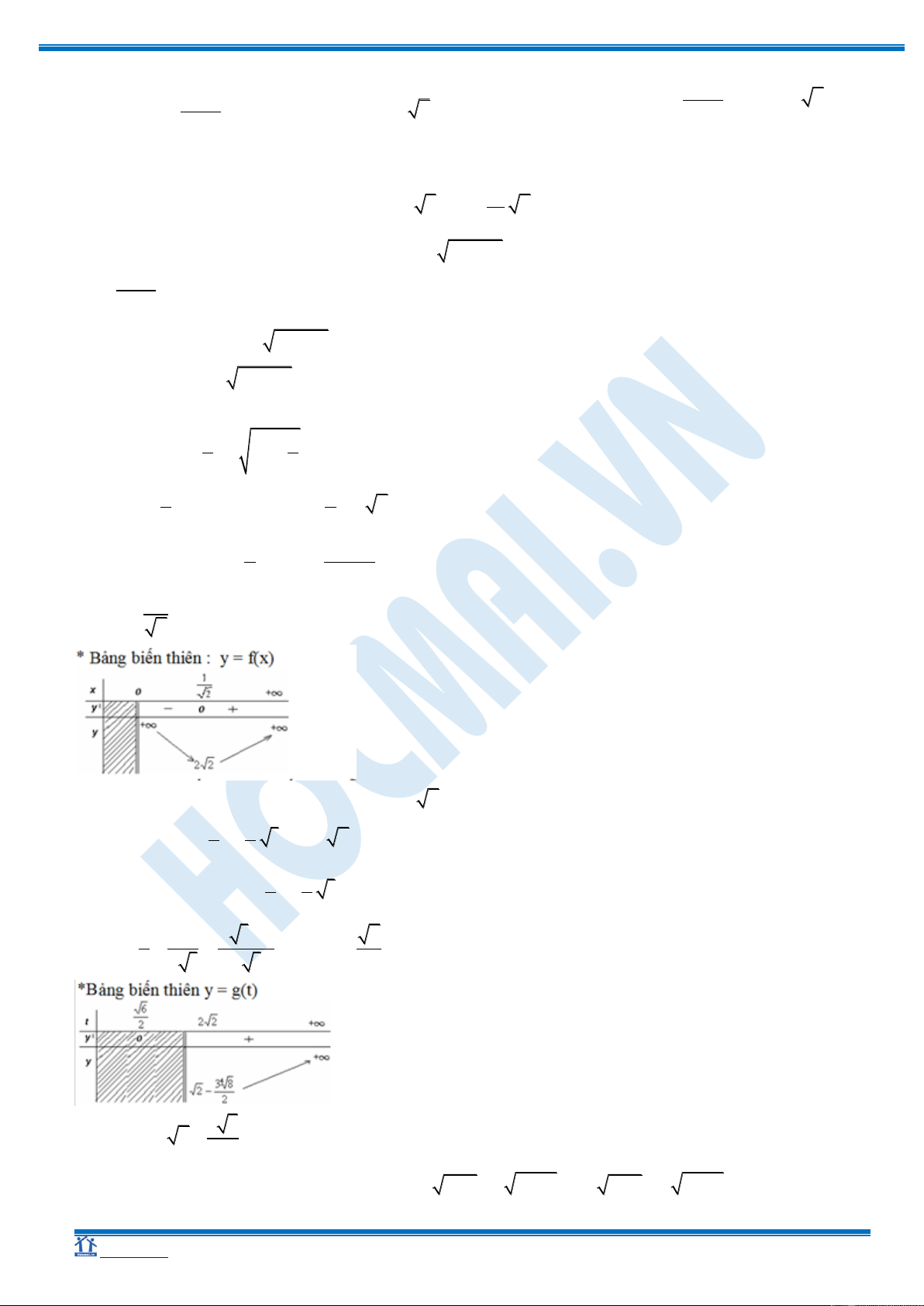
* Xét hàm số:
13
() 22
y g t t t
Có
1 3 4 6 6
'0
22
44
t
yt
tt
Vậy với
4
38
22
t
thì phương trình có hai nghiệm phân biệt.
Bài 3: Tìm m để phương trình sau có nghiệm:
22
44
1 2 1 1 2 1x x m x x
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com
Khóa học LTĐH KIT-1: Môn Toán – Thầy Lê Bá Trần Phương
Phương trình chứa căn
Hocmai.vn – Ngôi trường chung của học trò Việt
Tổng đài tư vấn: 1900 58-58-12
- Trang | 3 -
Giải:
Điều kiện:
1x
+ Với
1x
không là nghiệm
+ Với
1x
, phương trình
2
4
44
1 1 1
1 2 2
1 1 1
x x x
m
x x x







Đặt
41;1
1
xtt
x

Khi đó phương trình
22,1
21
tt
mt
t
Để phương trình đã cho có nghiệm thì 2 đồ thị:
22,1
21
tt
yt
t
ym

phải cắt nhau.
Xét
22,1
21
tt
yt
t

Ta có:
2
2
2 2 2
' 0; 1
(2 1)
tt
yt
t

Bảng biến thiên:
x
1 +
t’
+
t
+
1
Từ bảng biến thiên suy ra giá trị cần tìm là m > 1.
Bài 4: Tìm m để phương trình sau có nghiệm:
22
3 2 3 ( 1) 1x x m x x
Giải:
Phương trình
2 2 2
( 1) 2( 1) ( 1) 1x x m x x
2
2
11
2. 1
1
xx
m
x
x

( x = -1 không là nghiệm)
Đặt
2
1, 1 2
1
x
tt
x
2 2 3
11
'
1 (1 )
' 0 1
xx
tt
xx
tx


2
2
1
lim 1;
1
1
lim 1;
1
x
x
x
x
x
x



nên ta có
12t
Khi đó phương trình
2, 1 2t m t
t
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com