
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
247
NGHIÊN CỨU SỰ PHÂN BỐ CỦA HỆ SỐ ÁP LỰC HÔNG
TRONG MÁI DỐC
Phạm Phú Vinh, Nguyễn Thị Ngọc Hương
Trường Đại học Thủy lợi
1. GIỚI THIỆU CHUNG
Xác định áp lực hông của đất là một trong
những vấn đề cơ bản thường gặp trong địa kỹ
thuật. Trong bài toán phân tích ứng suất -
biến dạng của vật liệu, khái niệm hệ số áp lực
hông của đất, K, được đưa vào, trong đó K là
tỷ số giữa ứng suất theo phương ngang, σh,
trên ứng suất phương thẳng đứng, σv:
K = σh/σv (1)
Hệ số áp lực hông của đất được phân loại
theo trạng thái ứng suất trong đất thành hệ số
áp lực đất chủ động, Ka, hệ số áp lực đất bị
động, Kp, và hệ số áp lực đất tĩnh, K0. Lý
thuyết của Rankine trong đó áp dụng điều
kiện cân bằng giới hạn tại một điểm (Rankine
1857) và lý thuyết của Coulomb trong đó áp
dụng điều kiện cân bằng cố thể (Coulomb
1776) là hai cơ sở lý thuyết cơ bản đưa ra các
công thức tính Ka và Kp đang được sử dụng
rộng rãi hiện nay. Đối với hệ số áp lực đất
tĩnh K0, công thức để tính hệ số áp lực hông
đang được dùng phổ biến hiện nay phải kể
đến công thức của Jaky (Jaky 1944):
K0 = 1 sin φ (2)
trong đó: φ là góc ma sát trong của đất.
Như vậy với khối đất đang xét, trạng thái
của đất sẽ được xác định ở một trạng thái duy
nhất là “tĩnh”, “chủ động”, hay “bị động” và
áp dụng công thức tính các hệ số áp lực hông
tương ứng. Tuy nhiên khi áp dụng tính toán
vào trường hợp của một mái dốc, đi từ đỉnh
dốc xuống chân dốc, dưới tác dụng của trọng
lực, đất ở đỉnh dốc có xu hướng dồn xuống
chân dốc, làm cho trạng thái ứng suất của đất
có sự chuyển đổi giữa trạng thái chủ động và
bị động. Hiện nay đã có một số nghiên cứu
để đánh giá khảo sát sự thay đổi của hệ số áp
lực hông trong mái dốc và đã đạt được một
số kết quả nhất định. Tuy nhiên các nghiên
cứu về phạm vi thay đổi của hệ số áp lực
hông nằm ngoài các giá trị tính toán theo các
công thức hiện hành vẫn chưa được khảo sát
một cách toàn diện (Pipatpongsa, 2023).
Nghiên cứu này sẽ tập trung vào vấn đề
đánh giá sự phân bố giá trị hệ số áp lực hông
trong mái dốc, từ đó có thể có những nhận
định khái quát về việc phân định trạng thái
ứng suất chủ động hay bị động trong mái dốc.
2. PHƯƠNG PHÁP NGHIÊN CỨU
Để có được kết quả tính toán hệ số áp lực
hông theo công thức (1), trạng thái ứng suất
trong thân dốc được xác định bằng việc giải
phương trình quan hệ ứng suất - biến dạng
có dạng:
{σ} = [D].{ε} (3)
trong đó: {σ} là vector ứng suất, {ε} là vector
biến dạng, và [D] là ma trận độ cứng.
Bài báo này sử dụng tính năng phân tích
SIGMA/W của bộ phần mềm GEOSLOPE để
tính toán trạng thái ứng suất trong thân mái
dốc theo phương trình (3). Mô hình Mohr-
Coulomb đàn hồi tuyến tính hoàn toàn dẻo
được lựa chọn trong khai báo đầu vào của
tính toán. Các thông số mà mô hình cần dùng
để giải được phương trình (3) được liệt kê
trong Bảng 1.
Bài toán áp dụng cho một trường hợp mái
dốc điển hình với chiều cao thân dốc H = 5m,
hệ số mái dốc m = 1.5. Đồng thời bài toán
cũng sẽ tính toán thêm một số trường hợp với
các hệ số mái và chiều cao mái dốc thay đổi.
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
248
Bảng 1. Các thông số vật liệu
Chỉ tiêu Giá trị
Khối lượng đơn vị thể tích,
(kN/m3)17
Hệ số Poisson,
0.334
Mô đun biến dạng, E (kPa) 4000
Góc ma sát trong,
30
Lực dính đơn vị, c (kPa) 5
Góc giãn nở,
3
3. KẾT QUẢ
Kết quả tính toán phân bố hệ số áp lực
hông trong thân dốc với chiều cao 5m và hệ số
mái dốc 1.5 được thể hiện trong Hình 1. Kết
quả cho thấy giá trị hệ số áp lực hông nhỏ
nhất tính được trong khoảng 0.3 - 0.4, phân bố
thành một vùng tập trung trong thân dốc. Giá
trị K0 tăng dần khi điểm tính toán tiến ra phía
bề mặt mái dốc. Phạm vi giá trị lớn nhất tính
toán được trong khoảng 3.0 - 3.5 và tập trung
ở phạm vi đỉnh dốc và chân dốc.
Hình 1. Kết quả phân bố hệ số áp lực hông
cho trường hợp mái dốc cao 5m, hệ số mái 1.5
Khoảng tham chiếu cho giá trị của K0 có
thể được tính theo lý thuyết Rankine. Trường
hợp mặt đất nằm ngang Ka tính được là 0.3.
Trường hợp mặt đất nằm nghiêng với góc
dốc nhỏ hơn giá trị góc ma sát trong của đất,
Ka tính được là 0.6. Như vậy kết quả trong
Hình 1 cho thấy trong thân dốc có một vùng
tập trung của trạng thái “chủ động”. Ở phạm
vi đỉnh dốc và chân dốc, giá trị K0 tính được
vượt xa giá trị Kp tính theo lý thuyết Rankine.
Kết quả phân bố giá trị hệ số áp lực hông
trong thân dốc trường hợp tính toán này
tương đồng với kết quả tính được với mái
dốc có cùng hệ số m = 1.5 và thân dốc cao H
= 10 m đã được công bố trước đó. Và sự
phân bố giá trị của K trong thân dốc cho thấy
có sự đồng dạng với các kết quả đã công bố
khi hệ số mái dốc thay đổi.
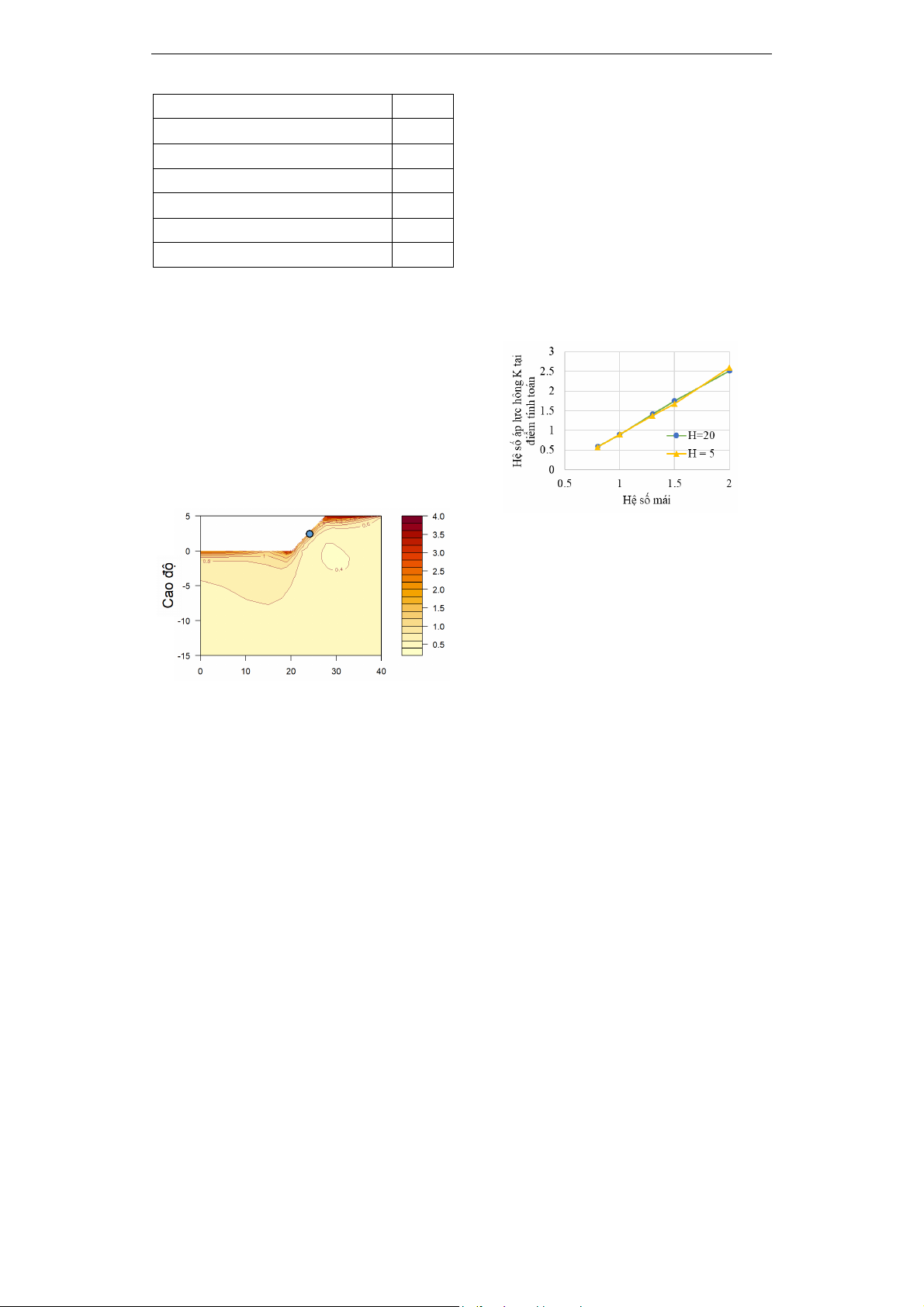
Để đánh giá định lượng sự ảnh hưởng của
hai thông số hình học của mái dốc, một điểm
tính toán được lựa chọn là điểm chính giữa
trên bề mặt mái dốc. Hệ số áp lực hông tại
điểm tính toán này được xác định với các mái
dốc có hệ số mái lần lượt là 0.8, 1, 1.3, 1.5 và
2. Chiều cao mái dốc được khảo sát là 5m, và
20m. Kết quả tính toán thể hiện trên Hình 2.
Hình 2. Giá trị hệ số áp lực hông
tại điểm tính toán khi hệ số mái
và chiều cao thân dốc thay đổi
Kết quả thể hiện trên Hình 2 cho thấy giá
trị hệ số áp lực hông tại điểm chính giữa trên
bề mặt mái dốc thay đổi khi hệ số mái dốc
thay đổi, và quan hệ này gần như là quan hệ
tuyến tính, và quan hệ này không bị ảnh
hưởng khi chiều cao thân dốc thay đổi và
được dự đoán chỉ phụ thuộc vào các chỉ tiêu
cơ lý của đất. Như vậy việc tính toán hệ số áp
lực hông có thể được đơn giản hóa bằng bài
toán tính cho mái dốc với chiều cao đơn vị,
và các điểm tính toán là các tọa độ tương đối.
Trong bài toán này, hệ số mái là thông số
hình học duy nhất của mái dốc có ảnh hưởng
kết quả tính toán.
Trong các lý thuyết cổ điển về áp lực đất
và hệ số áp lực hông của các tác giả Rankine
và Terzaghi, việc phân định trạng thái đất
thành “bị động”, chủ động”, “tĩnh” phù hợp
với các kết quả nghiên cứu thực nghiệm và
tính toán tại thời điểm nghiên cứu của các tác
Điểm tính toán

Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
249
giả. Hiện nay, sự phát triển của các công cụ
tính toán kết hợp với các kỹ thuật đo tiên tiến
hiện đại sẽ là những công cụ hữu ích để có
thể dự đoán gần đúng hơn trạng thái ứng suất
- biến dạng của đất. Đây cũng sẽ là hướng
nghiên cứu tiếp theo của báo cáo này để kiểm
chứng các kết quả tính toán được.
4. KẾT LUẬN
Kết quả tính toán giá trị hệ số áp lực hông
trong thân dốc của bài báo này xác nhận có
sự chuyển giao giữa trạng thái “chủ động” và
“bị động” trong thân dốc, như vậy việc tính
toán và áp dụng một giá trị là hằng số cho hệ
số áp lực hông trong thân dốc là không phù
hợp. Giá trị hệ số áp lực hông thay đổi theo
tọa độ điểm tính toán và phụ thuộc vào hệ số
mái dốc. Vai trò ảnh hưởng của chiều cao
thân dốc có thể được loại bỏ khi bài toán
chuyển về tính cho mái dốc với chiều cao
đơn vị và các tọa độ tính toán là tọa độ tương
đối của mái dốc. Ảnh hưởng của các chỉ tiêu
cơ lý của đất chưa được xét tới, do đó việc
mở rộng nghiên cứu để có được đánh giá
hoàn chỉnh về sự phân bố giá trị hệ số áp lực
hông trong mái dốc là cần thiết.
5. TÀI LIỆU THAM KHẢO
[1] Rankine, W. J. Macquorn. 1857. “On the
Stability of Loose Earth.” Philosophical
Transactions of the Royal Society of
London 147: 9-27. https://doi.org/10.1098/
rstl.1857.0003.
[2] Coulomb, C. A. 1776. “Essai Sur Une
Application Des Regles Des Maximis et
Minimis a Quelques Problemes de Statique
Relatifs a l’architecture.” Memoires de
l’Academie Royale Pres Divers Savants 7.
[3] Jaky, J. 1944. “The Coefficient of Earth
Pressure at Rest.” J. Soc. Hung. Archit.
Eng. 78: 355-88
[4] Pipatpongsa, Thirapong, Cheowchan
Leelasukseree, Kun Fang, Apipat Chaiwan,
and Natthawat Chanwiset. 2023. “Analysis
of Passive Thrust near Slope Toe in Laterally
Confined Slopes Lying on Inclined Bedding
Plane.” Bulletin of Engineering Geology
and the Environment 82 (12): 437.
https://doi.org/10.1007/s10064-023-03443-6
[5] Phạm Phú Vinh, Nguyễn Thu Nga, 2024,
“Ảnh hưởng của hệ số mái tới hệ số áp lực
hông của đất trong mái dốc.” Tạp chí Khoa
học Kỹ thuật Thủy lợi và Môi trường, Số
89: 128-133.


























