NỘI DUNG ÔN TẬP KIỂM TRA HỌC KỲ II
MÔN TOÁN - LỚP 11
A. HÌNH THỨC KIỂM TRA:
Tự luận (30%) kết hợp trắc nghiệm (70%); thời gian thi 60 phút.
B. NỘI DUNG
1. Trc nghim 14 câu (7,0 điểm):
- Phép tính lũy thừa, Phép tính logarit (3 câu)
• Viết li mt biu thc cha căn (dưi 3 du căn) dưi dng lũy thừa
• Tính gi tr ca 1 biu thc loga cha 1 tham s.
• Biu diễn 1 logarit qua hai logarit cho trưc.
- Bt phương trình mũ, logarit cơ bản: (3 câu)
• Vn dng: Bi ton thực tế v pt mũ hay pt logarit.
• Giải bpt mũ cơ bản (m l bc 2)
• Giải bpt loga cơ bản (biu thc dưi du loga l bc 1 hay bc 2)
- Đo hm, cc quy tắc tính đo hm (4 câu)
• Tính đo hm cp hai ca 1 hm s (đa thc, b1/b1) hoc tìm đo hm
cp 2 ti 1 đim cho trưc.
• Tính đo hm dng
u, u.v
v
(không s dng công thc tt, c th cha du
căn).
• Tính đo hm ca hm hợp.
• Đo hm ca hm s mũ hoc logarit.
- Hai đường thẳng vuông góc, hai mp vuông gc, khoảng cch, gc gia đường
thẳng v mt phẳng (4 câu).
• Tìm gc to bi đường thẳng v mp (c sn hình v).
TRƯỜNG THPT PHƯỚC LONG
Năm học: 2023 - 2024
• Tính gc to bi 2 mp cơ bản.
• Tính th tích khi chp hoc khi lăng tr khi biết đường cao v đy l
tam gic vuông, tam gic đu, hình vuông, hình ch nhật.
• Tính th tích khi chp, khi lăng tr. (vn dng )
2. T lun (3,0 điểm)
- Đo hm: (0,75 đim)
• Viết pttt ca đ th ca 1 hm s (
b1
b1
, đa thc) khi biết tiếp đim, honh
đ tiếp đim, tung đ tiếp đim hay biết hệ s gc.
- Phương trình v bt phương trình logarit: (0,75 điểm)
• Vn dng: Giải PT hoc bt phương logarit có sử dng phép biến đổi
loga ca tổng hoc tích.
- Khoảng cch, hai mt phẳng vuông gc (1,5 đim)
• Chng minh đường thẳng vuông góc vi mt phẳng, chng minh 2 đường
thẳng vuông góc, chng minh 2 mt phẳng vuông gc. (0,5 đim)
• Tính khoảng cch gia 2 đường thẳng chéo nhau, khoảng cch từ 1 đim
đến 1 mt phẳng (vn dng cao) (1,0 đim)
C. CÂU HỎI ÔN TẬP
A. TRẮC NGHIỆM
Câu 1. Biu thc
32
5
.P x x x x
==
(vi
0x
), giá tr ca
là
A.
1
2
. B.
5
2
. C.
9
2
. D.
3
2
.
Câu 2. Cho
a
là s thực dương,
và
3
3
log aa
. Mệnh đ no sau đây đúng?
ĐỀ SỐ 1
A.
1
3
=P
B.
3=P
C.
1=P
D.
9=P
Câu 3. Cho
22
log 3 , log 5ab
==
, khi đ
15
log 8
bằng
A.
3
+ab
B.
( )
3+ab
C.
( )
1
3+ab
D.
3
+ab
Câu 4. Giả sử nhiệt đ
( )
0
TC
ca mt vật giảm dần theo thời gian cho bi công thc
0,4
27 65 t
Te
−
=+
, trong đ thời gian
t
được tính bằng phút. Hỏi sau bao lâu nhiệt đ ca vật còn
li
0
37 C
?
A.
27
phút B.
4,68
phút C.
4,86
phút D.
37
phút
Câu 5. Cho bt phương trình
21 1 2
2
23
3
x x x− + −
có tập nghiệm
( )
;=S a b
. Giá tr ca
bằng
A.
2−
. B.
1−
. C. 1. D. 2.
Câu 6. Tập nghiệm ca bt phương trình
( )
2
3
log 36 3x−
là
A.
(
)
; 3 3;− − +
. B.
(
;3−
. C.
3;3−
. D.
(
0;3
.
Câu 7. Hàm s
32
31y x x x
= − + +
c đo hàm cp hai là
A.
66x−
. B.
2
3 6 1xx−+
. C.
62x−
. D.
32x−
.
Câu 8. Hàm s
1
1
x
yx
+
=−
c đo hàm cp hai là
A.
( )
2
2
"1
y
x
=− −
. B.
( )
( )
4
22
"1
x
y
x
−
=−
. C.
( )
3
4
"1
y
x
=−
. D.
( )
4
4
"1
y
x
=− −
.
Câu 9. Cho hàm s
( )
21=−f x x
. Tính
( )
1

f
.
A.
1−
. B.
1
. C.
3
2
. D.
0
.
Câu 10. Hàm s
sinx
yx
=
c đo hàm là
2
cos sinax x b x
yx
+
=
. Giá tr ca
P a b=+
là
A.
2P=−
B.
2P=
C.
0P=
D.
1P=
Câu 11. Hàm s
( )
2
2 1 1y x x= + +
c đo hàm là
A.
2
2
1
x
x+
B.
2
2
2 2 3
1
xx
x
++
+
C.
2
2
42
1
xx
x
++
+
D.
2
2
1
x
x
−
+
Câu 12. Tìm đo hàm ca hàm s
5
3x
y=
.
A.
5
3 .ln3
x
y=
B.
5
5.3 x
y=
C.
5.3 .ln3
x
y=
D.
5
5.3 .ln3
x
y=
Câu 13. Tìm đo hàm ca hàm s
( )
2
ln 1 x
ye=+
.
A.
( )
2
2
2
2
1
x
x
e
y
e
−
=+
. B.
2
21
x
x
e
ye
=+
. C.
2
1
1
x
ye
=+
. D.
2
2
2
1
x
x
e
ye
=+
.
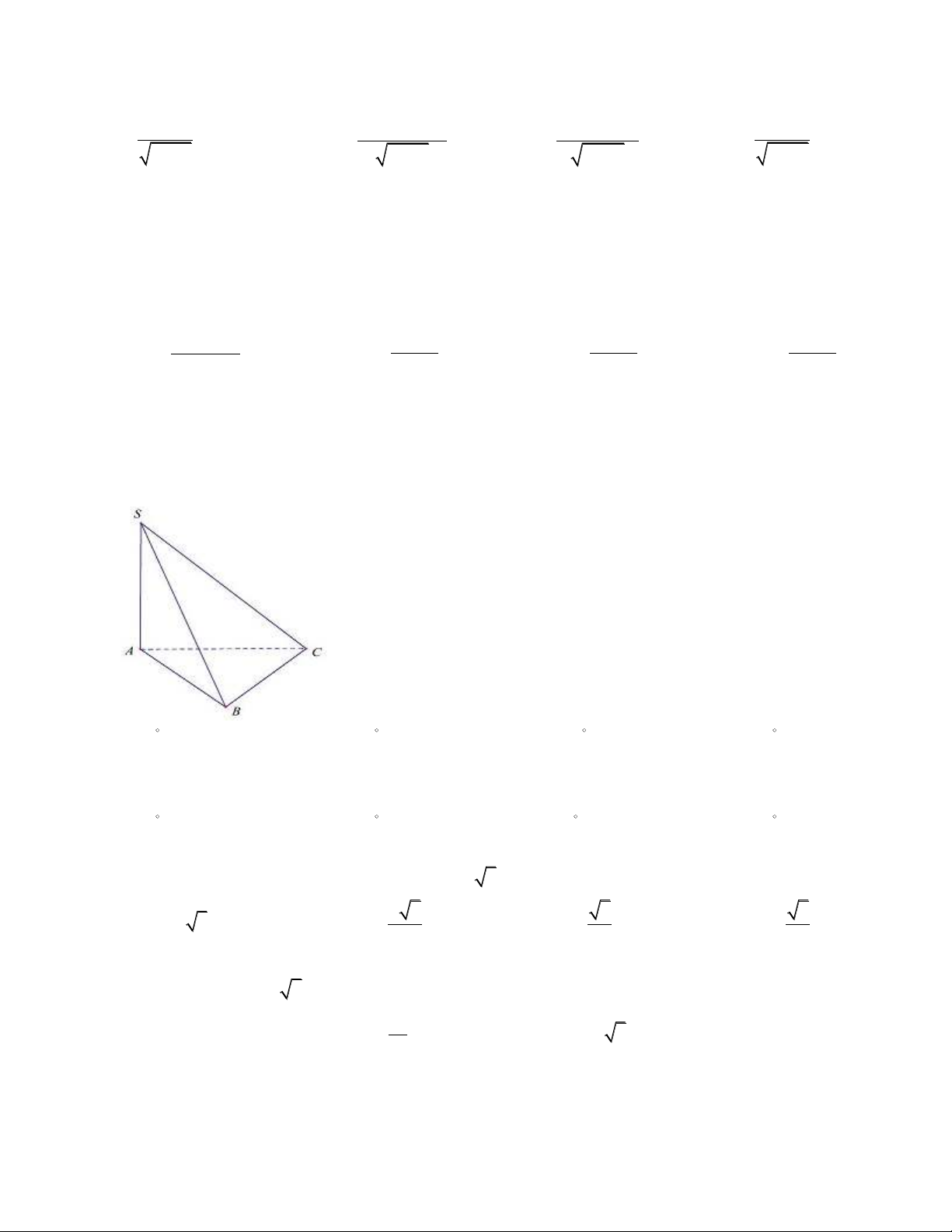
Câu 14. Cho hình chóp
.S ABC
có
( )
SA ABC⊥
, tam giác
ABC
đu cnh
a
và
SA a=
(tham khảo hình v bên). Tìm góc gia đường thẳng
SC
và mt phẳng
( )
ABC
.
A.
60
. B.
45
. C.
135
. D.
90
.
Câu 15. Cho hình chóp
.S ABCD
c đy l hình ch nhật cnh
AB a=
,
SA
vuông góc
vi mt phẳng đy v
2SB a=
. Góc gia mt phẳng
( )
SBC
mt phẳng đy bằng
A.
90
. B.
60
. C.
45
. D.
30
.
Câu 16. Cho hình chóp
.S ABC
có tam giác
ABC
vuông ti
A
,
, 2 .AB a AC a==
SA
vuông góc vi mt phẳng đy
()ABC
và
3=SA a
. Tính th tích
V
ca khi chóp
S.ABC
.
A.
33=Va
. B.
3
23
3
=Va
. C.
3
3
3
=Va
. D.
3
3
4
=Va
.
Câu 17. Cho khi chóp
.S ABC
c đy
ABC
l tam gic đu cnh
2a
. Cnh bên vuông
góc vi đy v
3=SA a
. Tính th tích
V
ca khi chóp
.S ABC
.
A.
3
3=Va
. B.
3
4
=a
V
. C.
33=Va
. D.
3
=Va
.
Câu 18. Cho hình chóp
.S ABCD
c đy
ABCD
là hình ch nhật có
, 4AB a BC a==
,
cnh bên
SA
vuông góc vi mt phẳng đy v
2SA a=
. Tính th tích
V
ca hình chóp
.S ABCD
.
A.
32
6
a
V=
. B.
32
4
a
V=
. C.
3
42Va=
. D.
3
42
3
a
V=
.
Câu 19. Cho khi chóp
.S ABCD
c đy
ABCD
là hình vuông cnh
3a
, cnh
SA
vuông
góc vi mt phẳng
( )
ABCD
và
3SA a=
. Tính th tích
V
ca khi chóp
.S ABCD
.
A.
3
9Va=
. B.
3
3
4
a
V=
. C.
3
9
2
a
V=
. D.
3
3Va=
.
Câu 20. Cho khi lăng tr đng
.ABC A B C
c đy l tam gic đu cnh
3a
và
'2AA a=
. Th tích ca khi lăng tr
.ABC A B C
bằng
A.
3
33
4
a
. B.
3
93
2
a
. C.
33
4
a
. D.
33a
.
Câu 21. Cho khi lăng tr đng
.ABC A B C
có
0
60=BAC
;
2=AB a
;
3=AC a
và
'9=AA a
. Th tích ca khi lăng tr
.ABC A B C
bằng
A.
3
2
a
. B.
3
a
. C.
3
9
2
a
. D.
3
27
2
a
.
Câu 22. Cho hình lăng tr đng
.ABCD A B C D
c đy
ABCD
l hình ch nhật,
AB a
,
2AD a
,
5AB a
. Tính theo
a
th tích
V
ca khi lăng tr đã cho.
A.
32Va
. B.
3
22Va
. C.
310Va
. D.
3
22
3
a
V
.
Câu 23. Cho hình chóp
.S ABCD
c đy
ABCD
là hình thoi cnh
a
, góc
0
120=BAD
.
Cnh bên
SA
vuông góc vi đy
( )
ABCD
và
SD
to vi đy
( )
ABCD
mt góc
0
60
. Tính
theo
a
th tích
V
ca khi chóp
.S ABCD
.
A.
3
4
=a
V
. B.
3
3
4
=a
V
. C.
3
2
=a
V
. D.
3
=Va
.
B. TỰ LUẬN