
NỘI DUNG ÔN TẬP KIỂM TRA HỌC KÌ II
MÔN TOÁN - LỚP 12
A. HÌNH THỨC KIỂM TRA:
Trắc nghiệm (100%); thời gian thi 90 phút.
B. NỘI DUNG: Trc nghim 50 câu (10,00 điểm):
1. Đại số và giải tích:
Đại số và giải tích : Nguyên hm, tích phân; ứng dụng(Hnh hc, vt l) của
tích phân; Số phức.
2. Hình học
Hình học: Hệ trục ta độ, PT Mặt phẳng, PT đường thẳng, PT mặt cầu.
C. CÂU HỎI ÔN TẬP
ĐỀ CƯƠNG ÔN THI HK2 MÔN TOÁN KHỐI 12 NĂM HỌC 2023-2024
PHẦN NHẬN BIẾT-THÔNG HIỂU
NGUYÊN HÀM -TÍCH PHÂN-ỨNG DỤNG
Câu 1. Trên khoảng , h nguyên hàm của hàm số là
A. . B. .
C. . D. .
Câu 2. Cho hàm số . Khẳng định no dưới đây đúng?
A. . B. .
C. . D. .
Câu 3. Cho hàm số . Khẳng định no dưới đây đúng?
A. . B. .
C. . D. .
( )
0; +
( )
3
2
f x x=
( )
1
2
3
2
f x dx x C=+
( )
2
5
5
2
f x dx x C=+
( )
5
2
2
5
f x dx x C=+
( )
1
2
2
3
f x dx x C=+
( )
23f x x=+
( )
33f x dx x x C= + +
( )
2f x dx x C=+
( )
23f x dx x x C= + +
( )
3
3
3
x
f x dx x C= + +
( ) 2 1f x x=−
2
( ) (2 1) 2 1
3
f x dx x x C= − − +
1
( ) (2 1) 2 1
3
f x dx x x C= − − +
1
( ) 2 1
3
f x dx x C= − − +
1
( ) 2 1
2
f x dx x C= − +
TRƯỜNG THPT PHƯỚC LONG
Năm học: 2023 - 2024
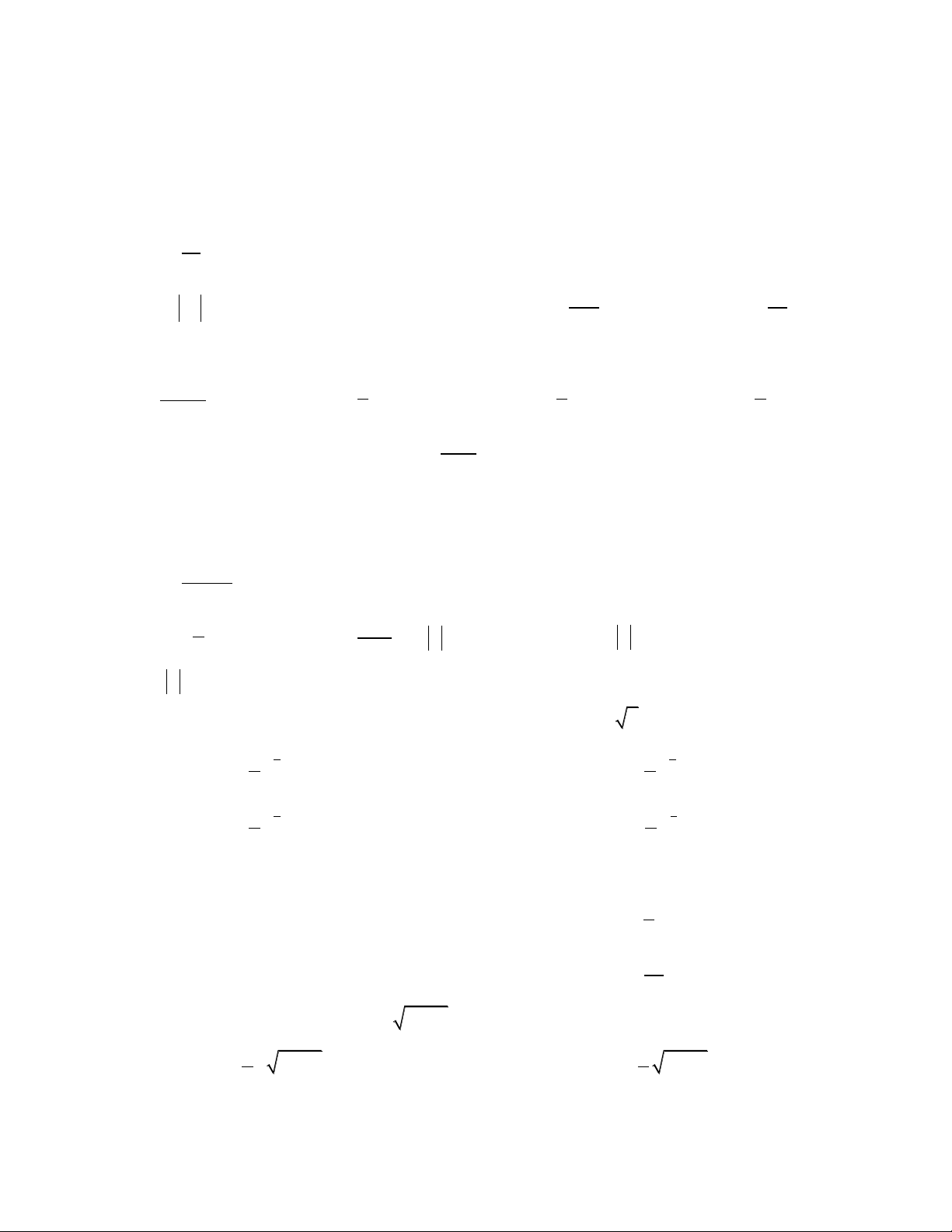
Câu 4. Cho bằng
A. . B. . C. . D.
.
Câu 5. bằng
A. . B. . C. . D. .
Câu 6. H nguyên hàm của hàm số là
A. . B. . C. . D. .
Câu 7. H nguyên hàm của hàm số trên là
A. . B. .
C. . D. .
Câu 8. bằng
A. . B. . C. . D.
.
Câu 9. Trên khoảng , h nguyên hàm của hàm số là
A. . B. .
C. . D. .
Câu 10. Cho hàm số . Khẳng định no dưới đây đúng?
A. . B. .
C. . D. .
Câu 11. Cho hàm số . Khẳng định no dưới đây đúng?
A. . B. .
( )
2f x dx
( )
2f x dx
( )
2f x dx
( )
+
2f x dx
( )
2.x f x dx
3
1dx
x
+
3
ln xC
+3lnxC
−+
2
1
2C
x
−+
2
1C
x
( )
=3
2x
f x e
+
+
+
31
2
31
x
eC
x
+
2
3
x
eC
+
3
1
3
x
eC
+
3
2
3
x
eC
( )
=−
2
1
x
fx x
( )
+1;
( )
− − +2 4ln 1x x C
( )
+ − +2ln 1x x C
( )
− + +2 4ln 1x x C
( )
+ − +2 2ln 1x x C
+
1
x
xe dx
x
++
1
x
eC
x
++
2
ln
2
x
xe xC
++ln
x
xe x C
++ln
x
e x C
( )
0; +
( )
=f x x x
( )
1
2
3
2
f x dx x C=+
( )
2
5
5
2
f x dx x C=+
( )
5
2
2
5
f x dx x C=+
( )
1
2
2
3
f x dx x C=+
( ) ( )
=−32f x x x
( )
= − +
32
3f x dx x x C
( )
= − +
2
3( 1)
2
f x dx x x C
( )
= − +
22
3 ( )f x dx x x x C
( )
= − +
3
2
3
3
x
f x dx x C
=+
2
( ) 2 1f x x x
= + +
2
2
( ) 1
3
f x dx x x C
= + +
2
2
( ) 1
3
f x dx x C

C. . D. .
Câu: (Đề Tham Khảo 2017) Tìm nguyên hàm của hàm số .
A. . B. .
C. . D. .
Câu 12. (Chuyên Bc Ninh 2019) Nếu thì hàm số bằng
A. . B. .
C. . D. .
Câu 13. (THPT Yên Phong 1 Bc Ninh 2019) Hàm số là một nguyên hàm
của hàm số no sau đây trên ?
A. . B. . C. . D.
.
Câu 14. (THPT - Yên Định Thanh Hóa 2019) Tìm nguyên hàm của hàm số
.
A. . B. .
C. . D. .
Câu 15. (THPT Hong Hoa Thm Hưng Yên 2019) Nguyên hàm của hàm số
là
A. . B. . C. . D. .
Câu 16. (Chuyên Bc Giang 2019) Hàm số là nguyên hàm của hàm số nào
trong các hàm số sau:
A. . B. . C. . D.
.
( )
= + +
3
2
2
( ) 1
3
f x dx x C
( )
= + +
3
2
1
( ) 1
2
f x dx x x C
( )
2
2
2
f x x x
=+
( )
31
d3
x
f x x C
x
= + +
( )
32
d3
x
f x x C
x
= − +
( )
31
d3
x
f x x C
x
= − +
( )
32
d3
x
f x x C
x
= + +
( )
32
d4f x x x x C= + +
( )
fx
( )
3
4
3
x
f x x Cx= + +
( )
2
12 2f x x x C= + +
( )
2
12 2f x x x=+
( )
3
4
3
x
f x x=+
( )
3
1
3
F x x=
( )
;− +
( )
2
3f x x=
( )
3
f x x=
( )
2
f x x=
( )
4
1
4
f x x=
( )
4
2
2x
fx x
+
=
( )
31
d3
x
f x x C
x
= − +
( )
32
d3
x
f x x C
x
= + +
( )
31
d3
x
f x x C
x
= + +
( )
32
d3
x
f x x C
x
= − +
21
ex
y−
=
21
2e xC
−+
21
exC
−+
21
1e
2
xC
−+
1e
2
xC+
( )
2
x
F x e=
2
( ) 2 x
f x xe=
2
2
( ) 1
x
f x x e=−
2
() x
f x e=
2
() 2
x
e
fx x
=

Câu 17. (Sở Phú Thọ 2019) Cho là một nguyên hàm của trên khoảng
( )
1; +
thỏa mãn . Tìm .
A. B. C. D.
Câu 18. (Mã 101 – 2020 Lần 2) Biết là một nguyên hàm của hàm số
trên . Khi đó bằng
A. B. C. D.
Câu 19. (THPT Gia Lộc Hải Dương 2019) H nguyên hàm của hàm số
là
A. . B. .
C. . D. .
Câu 20. Cho biết . Tính giá trị biểu thức:
.
A. 12. B. 13. C. 14. D. 15.
Câu 21. Cho hàm số có đạo hàm là và .
Biết là nguyên hàm của thỏa mãn , khi đó bằng
A. . B. . C. . D. .
Câu: Cho hàm số liên tục, có đạo hàm trên . Tích phân
bằng
A. B. C. D.
Câu 22. Hàm số (với là một nguyên hàm của hàm số nào sau đây?
A. B. C. D.
Câu 23. Hàm số là một nguyên hàm của hàm số:
( )
Fx
( )
1
1
=−
fx x
( )
14+=Fe
( )
Fx
( )
2ln 1 2−+x
( )
ln 1 3−+x
( )
4ln 1−x
( )
ln 1 3−−x
( )
2x
F x e x=+
( )
fx
( )
2f x dx
2
2 2 .
x
e x C++
22
1.
2
x
e x C++
22
12.
2
x
e x C++
22
4.
x
e x C++
( ) ( )
21
x
f x x e=−
( )
23−+
x
x e C
( )
23++
x
x e C
( )
21++
x
x e C
( )
21−+
x
x e C
2
4 11 dx ln 2 ln 3
56
xa x b x C
xx
+= + + + +
++
22
P a ab b= + +
( )
y f x=
( )
2
12 2,f x x
=+
x
( )
13f=
( )
Fx
( )
fx
( )
02F=
( )
1F
3−
1
2
7
( )
fx
( ) ( )
1;2 ,f 1 8;f 2 1− − = = −
( )
2
1
f ' x dx
−
1.
7.
9.−
9.
( )
1
F x x x
=+
0)x
( )
1.fx=
( )
2
1
1.fx x
=+
( )
2
ln | |
2.
x
f x x=+
( )
2
1
1.fx x
=−
( )
2sinF x x x=+

A. .
B. .
C. .
D. .
Câu 24. Nguyên hàm của hàm số là:
A. .
B. .
C. .
D. .
Câu 25. Tính
cos(5 4)x dx−
, kết quả là
A.
1sin(5 4)
5xC− − +
. B.
1sin(5 4)
5xC−+
.
C.
5sin(5 4)xC− − +
. D.
5sin(5 4)xC−+
.
Câu 26. Tính
1
(sin )x dx
x
+
, kết quả là
A.
cos lnx x C++
. B.
cos lnx x C− + +
.C.
2
1
cos xC
x
− − +
D.
cos lnx x C− + +
.
Câu 27. Tính
2sin cosx xdx
, kết quả là
A.
2cos2xC−+
. B.
1cos2
2xC
+
. C.
2cos2xC+
. D.
1cos2
2xC−+
.
Câu 28. Tính
( 1)sinx xdx+
, kết quả là
A.
( 1)cos sinx x x C+ + +
. B.
( 1)sin cosx x x C− + + +
.
C.
( 1)cos sinx x x C− + + +
. D.
( 1)cos sinx x x C− + − +
.
Câu 29. Tìm một nguyên hàm F(x) của hàm số
2
( ) ( 0)
b
f x ax x
x
= +
, biết rằng
( )
11F−=
,
( ) ( )
1 4, 1 0Ff==
A.
2
2
3 3 7
() 44
x
Fx x
= + −
. B.
2
3 3 7
() 4 2 4
x
Fx x
= + +
.C.
2
2
3 3 1
() 22
x
Fx x
= − −
. D.
2
3 3 7
() 4 2 4
x
Fx x
= + −
.
Câu 30. H nguyên hàm của hàm số
( )
x
f x e x=+
là
A.
2
1.
2
++
x
e x C
B.
2.++
x
e x C
C.
2
11 .
12
++
+
x
e x C
x
D.
1.++
x
eC
( )
3
1cos
3
f x x x=−
( )
2 cosf x x x=+
( )
2 cosf x x x=−
( )
3
1cos
3
f x x x=+
( )
3
29f x x=−
4
49x x C−+
4
1
4xC+
4
19
2x x C−+
3
49x x C−+



![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)










![Phiếu bài tập cuối tuần Tiếng Việt 1 tuần 2 đề 2: [Hướng dẫn chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250728/thanhha01/135x160/42951755577464.jpg)

