TRƯỜNG THCS THÀNH CÔNG
NHÓM TOÁN 9
NĂM HỌC 2023 - 2024
NỘI DUNG ÔN TẬP GIỮA HỌC KÌ 1
Môn: Toán 9
I. NỘI DUNG:
A. Đại số
1. Chương I:
*Bài toán rút gọn biểu thức và các câu hỏi liên quan:
- Tính giá trị biểu thức khi cho giá trị x
- Rút gọn biểu thức
- Tìm x
- Tìm số nguyên x để biểu thức có giá trị nguyên
2. Chương II:
* Bài toán về hàm số y=ax+b:
- Vẽ đồ thị hàm số
- Tìm tọa độ giao điểm của hai đường thẳng
- Ba đường thẳng đồng quy
B. Hình học
1. Chương I:
- Hệ thức lượng
- Bài toán thực tế tính chiều cao, khoảng cách
2. Chương II:
- Sự xác định đường tròn
- Đường kính và dây cung
II. BÀI TẬP THAM KHẢO:
A. ĐẠI SỐ:
Dạng 1. Bài toán rút gọn biểu thức và các câu hỏi liên quan
Bài 1. Cho hai biểu thức
2
2
x
Ax
và
12
:
44
2
xx
Bxx
x






với
0; 4xx
a) Tính giá trị của
A
khi
.
b) Rút gọn biểu thức
B
.
c) Tìm
x
nguyên để
. – 2C A B
có giá trị nguyên.
Bài 2. Cho hai biểu thức:
38
4
22
x x x
Px
xx

và
1
2
Qx
với
0; 4xx
a) Tính giá trị biểu thức Q khi
7 4 3x
b) Rút gọn biểu thức P.
c) Tìm tất cả các giá trị nguyên của x để
P
MQ
đạt giá trị nguyên.
Bài 3. Cho hai biểu thức
24
6
Nx
và
1 17 30
36
66
xx
Mx
xx

với
0, 36.xx
1) Tính giá trị của biểu thức
N
khi
9x
2) Rút gọn biểu thức
M
3) Tìm số nguyên
x
để biểu thức
.L N M
có giá trị nguyên lớn nhất.
Bài 4. Cho hai biểu thức
2 1 3 11 3
;
9
3 3 2
x x x x
AB
x
x x x
với
0 9.x
a) Tính giá trị
B
tại
25;x
b) Rút gọn
;A
c) Tìm số nguyên
x
để
.P A B
là số nguyên.
Bi 5. Cho hai biểu
2
x
A
x
thức
11
. 3 2
22
x
B x x
x x x





với x > 0; x ≠ 4
a) Tính giá trị A tại
36;x
b) Rt gọn B
c) Tm giá trị nguyên của x để M = A.B c giá trị nguyên.
Bài 6. Cho biểu thức
3 6 4
1
11
xx
Px
xx

với
0; 1xx
a) Rút gọn P.
b) Tính giá trị của P khi
x = 64
c) Tm giá trị nguyên của x để biểu thức P có giá trị nguyên.
Bài 7. Cho hai biểu thức
21
xx
Mxx

;
1 1 2
1
xx
Nx x x x


với
0; 1xx
a) Tính giá trị của M khi
x9
b) Rút gọn N.
c) Tm giá trị nguyên của x để biểu thức
M
PN
có giá trị nguyên.
Bài 8. Cho hai biểu thức
25
12
Ex x x

;
3
1
12
x
F
xx
 
với
0; 1xx
.
a) Rút gọn các biểu thức E, F.
b) Tm giá trị nguyên của x để biểu thức
:G E F
có giá trị nguyên.
Bài 9. Cho hai biểu thức
1 1 1
:xx
Gx
x x x x








;
2
1
x
Hx
với
0; 1xx
.
a) Tính giá trị của H khi
x 25
b) Rút gọn các biểu thức G.
c) Tm giá trị nguyên của x để biểu thức
.I G H
có giá trị nguyên
Dạng 2: Bài toán về hàm số y=ax+b
Bài 1. Vẽ đồ thị của hai hàm số sau trên cùng một mặt phẳng toạ độ:
a)
2yx
và
3,5yx
b)
21yx
và
21yx
c)
5yx
và
1
2
yx
d)
yx
và
1
12
yx
e)
3yx
và
11
3
yx
f)
2,5 5yx
và
2,5 5yx
Bài 2. Cho đường thẳng
1: 2 3d y x
và
2: 3 7d y x
Tìm tọa độ giao điểm của
1
d
và
2
d
.
Bài 3. Cho các hàm số:
21yx
và
5yx
a) Vẽ đồ thị của các hàm số đã cho trên cùng một hệ trục tọa độ.
b) Xác định tọa độ giao điểm C của đồ thị hai hàm số trên.
b) Chứng tỏ điểm C cũng thuộc đường thẳng
1: 3 3d y x
Bài 4. Cho ba đường thẳng:
1 2 3
11
: ; : 1; : 2 1.
22
d y x d y x d y x
a) Vẽ các đường thẳng
1
d
,
2
d
và
3
d
trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của
1
d
và
2
d
.
c) Các đường thẳng
1
d
,
2
d
và đường thẳng
4
3
:2
2
d y x
có đồng quy không?
Bài 5. Cho ba đường thẳng
1 2 3
1
: 3 ; : ; : 4
3
d y x d y x d y x
a) Vẽ các đường thẳng
1
d
,
2
d
và
3
d
trên cùng mặt phẳng tọa độ.
b) Gọi A, B lần lượt là giao điểm của
3
d
với
1
d
và
3
d
với
2
d
. Tìm tọa độ của A và B.
Bài 6. Các đường thẳng sau đây c đồng quy không?
a)
1: 3 1d y x
và
2:d y x
,
3
1
:2
d y x
.
b)
1: 1 0d x y
và
2: 5 5d y x
,
3
15
:0
33
d x y
.
Bài 7. Cho hai đường thẳng
1
d
:
y = mx + 2
và
2
d
:
1
y = x -1
2
.
a) Với
1
2
m
, xác định toạ độ giao điểm của
1
d
và
2
d
.
b) Xác định giá trị của m để
( 3; 3)M
là giao điểm của
1
d
và
2
d
.
Bài 8. Gọi
1
d
là đồ thị hàm số
y = mx - 2
và
2
d
là đồ thị hàm số
11
2
yx
.
a) Với
1
3
m
, xác định toạ độ giao điểm của
1
d
và
2
d
.
b) Xác định giá trị của m để
( 2;1)M
là giao điểm của
1
d
và
2
d
.
Bài 9. Với giá trị nào của m th đồ thị hàm số
32y x m
và đường thẳng
4 5 2y x m
cắt
nhau tại một điểm trên trục tung.
B. HÌNH HỌC:
Dạng 1. Bài toán thực tế tính chiều cao, khoảng cách.
Bài 1. Một cầu trượt trong công viên c độ dốc là 28° và c độ cao là 2,1 cm. Tính độ dài của mặt cầu trượt
(làm tròn đến chữ số thập phân thứ nhất).
Bài 2. Để đo chiều rộng AB của một con sông mà không phải
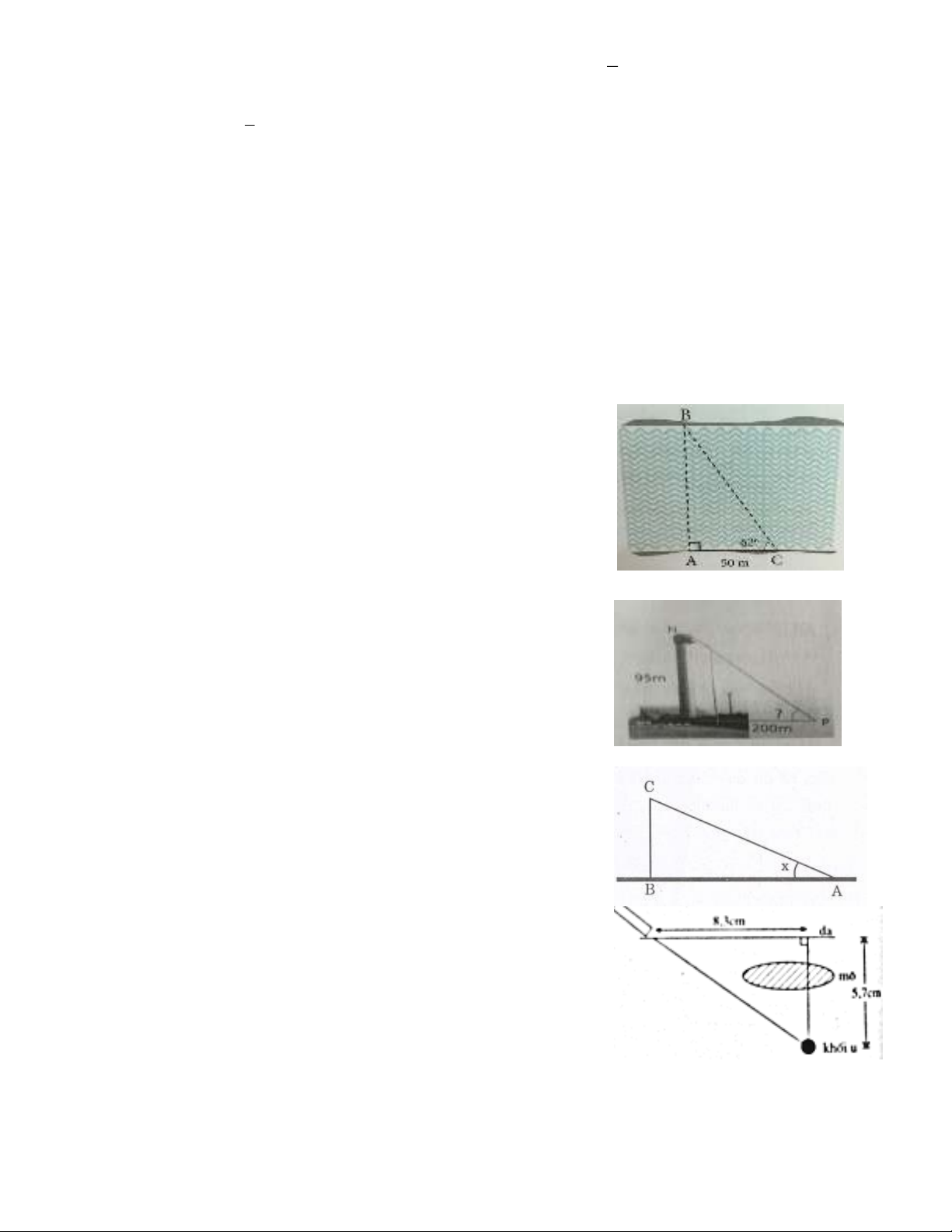
băng ngang qua n, một người chọn vị trí đo là điểm C sao
cho AC = 50m. Từ C, người đ nhìn thấy B với một góc
ngắm 62o với bờ sông. Tính bề rộng của con sông
Bài 3. Ngọn hải đăng quan sát trên đảo Cô Tô cao 105m. Ở một
thời điểm nào đ vào ban ngày, người ta đo được bóng của
ngọn hải đăng trên mặt đất dài 250m. Hỏi lúc đ gc tạo bởi
tia sáng mặt trời và mặt đất là bao nhiêu?
Bài 4. Một máy bay phản lực cất cánh từ vị trí A, bay lên với một
góc x = 30° so với phương nằm ngang, sau một khoảng thời
gian 15 giây máy bay đạt được cao độ là BC = 3000 mét. Tính
vận tốc trung bnh của máy bay (làm tròn đến hàng đơn vị).
Bài 5. Bác sĩ cần chiếu một chùm tia gamma để tiêu diệt khối u
nằm dưới da 5,7cm. Để tránh làm tổn thương mô, bác sĩ đặt
nguồn tia cách khối u (trên mặt da) cách vị trí khối u 8,3cm
(như hnh vẽ)
a) Hỏi góc tạo bởi chùm tia với mặt da?
b) Chùm tia phải đi một đoạn dài bao nhiêu để đến được
khối u?
Bài 6. Một người c mắt cách mặt đất 1,4m, đứng cách tháp
Eiffel 400m nhn thấy đỉnh tháp với gc nâng 39o. Tính
chiều cao của tháp ( làm tròn đến mét ).
Bài 7. Hai ngư dân đứng ở bên một bờ sông cách nhau 250m
cùng nhn thấy một cù lao trên sông với các gc nâng lần
lượt là 30o và 40o. Tính khoảng cách d từ bờ sông đến cù
lao.
Bài 8. Tính chiều cao của một ngọn ni cho biết tại hai điểm
cách nhau 1km trên mặt đất người ta nhn thấy đỉnh ni
với gc nâng lần lượt là 40o và 32o.
Bài 9. Một cái tháp được bên bờ một con sông, từ một điểm đối
diện với tháp ngay bờ bên kia người ta nhìn thấy đỉnh tháp
với góc nâng 60o. Từ một điểm khác cách điểm ban đầu
20m người ta cũng nhn thấy đỉnh tháp với góc nâng 30o.
Tính chiều cao của tháp và bề rộng của sông
Dạng 2. Đường kính và dây cung
Bài 1. Cho tam giác ABC có trực tâm H và nội tiếp đường tròn (O) đường kính AD.
a) Chứng minh BHCD là hình bình hành.
b) Kẻ đường kính OI vuông góc BC tại I. Chứng minh Ị, H, D thẳng hàng.
c) Chứng minh AH = 2OI.
Bài 2. Cho tam giác ABC (AB < AC) c hai đường cao BD và CE cắt nhau tại trực tâm H. Lấy I là trung
điểm của BC.
a) Gọi K là điểm đối xứng của H qua I. Chứng minh tứ giác BHCK là hình bình hành.
b) Xác định tâm O của đường tròn qua các điểm A, B, K, C.
c) Chứng minh OI và AH song song.
Bài 3. Cho điểm A nằm trên đường tròn (O) có CB là đường kính và AB < AC. Vẽ dây AD vuông góc với
BC tại H. Chúng minh:
a) Tam giác ABC vuông tại A.
b) H là trung điểm AD, AC = CD và BC là tia phân giác góc ABD;