TOÁN 11-CÁNH DIỀU Điện thoại: 0946798489
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
PHẦN A. LÝ THUYẾT VÀ VÍ DỤ MINH HỌA
I. GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
Cho đường thẳng
d
và mặt phẳng
( )P
, ta có định nghĩa sau:
Kiến thức trọng tâm
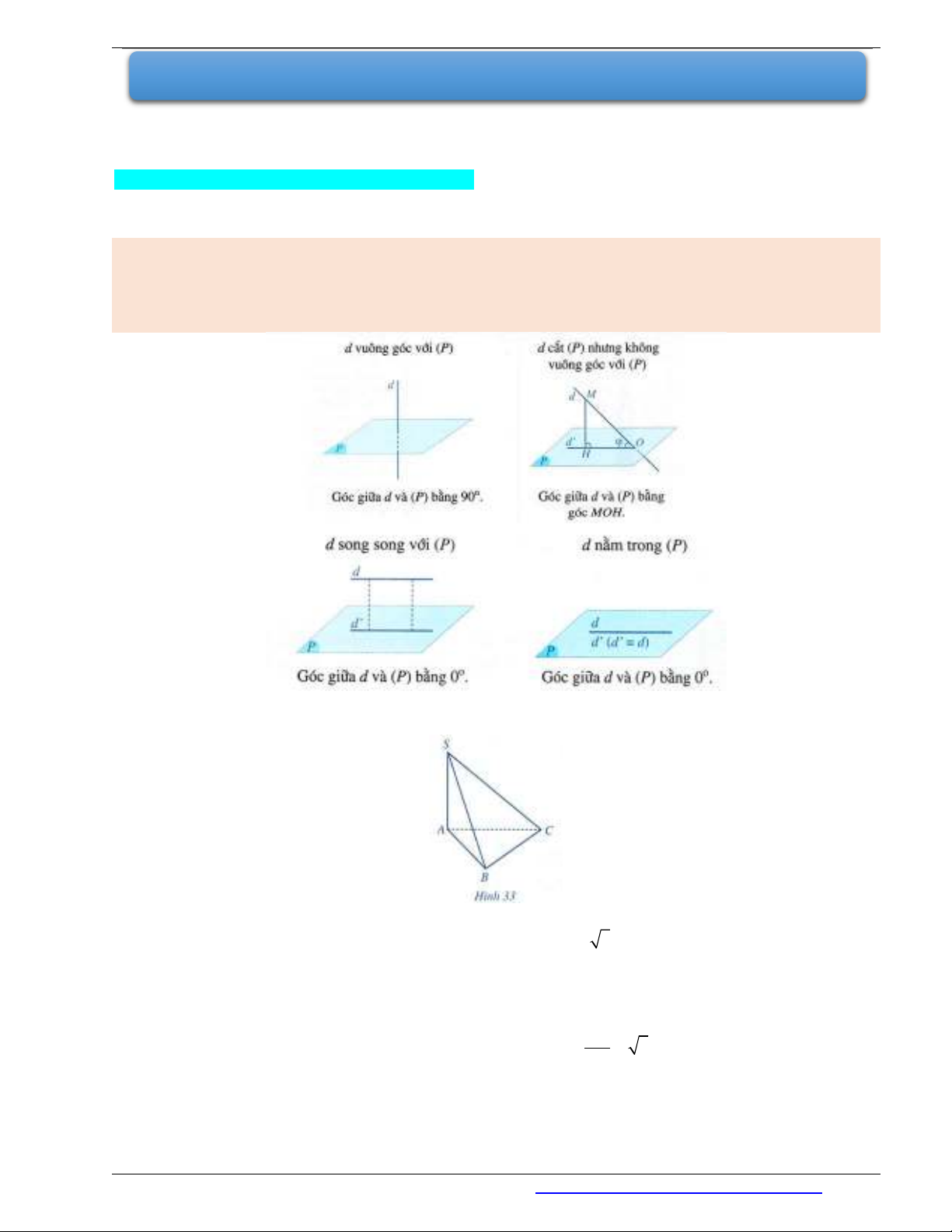
- Nếu đường thẳng
d
vuông góc với mặt phẳng
( )P
thì góc giữa
d
và
( )P
bằng
90
.
- Nếu đường thẳng
d
không vuông góc với mặt phẳng
( )P
thì góc giữa đường thẳng
d
và mặt phẳng
( )P
là góc giữa
d
và hình chiếu
d
của đường thẳng
d
trên
( )P
.
Nhận xét: Góc giữa đường thẳng và mặt phẳng có số đo từ
0
đến
90
.
Ví dụ 1. Cho hình chóp
.S ABC
có
SA
(ABC) (Hình 33).
a) Tính góc giữa đường thẳng
SA
và mặt phẳng
( )ABC
.
b) Tính góc giữa đường thẳng
SB
và mặt phẳng
( )ABC
, biết
3SA AB
.
Giải
a) Vì
( )SA ABC
nên góc giữa đường thẳng
SA
và mặt phẳng
( )ABC
bằng
90
.
b) Vì
( )SA ABC
nên
AB
là hình chiếu của
SB
trên
( )ABC
. Suy ra góc giữa đường thẳng
SB
và mặt
phẳng
( )ABC
bằng
SBA
. Xét tam giác vuông
SBA
. Vì
tan 3
SA
SBA AB
nên
60SBA
. Vậy góc giữa
đường thẳng
SB
và mặt phẳng
( )ABC
bằng
60
.
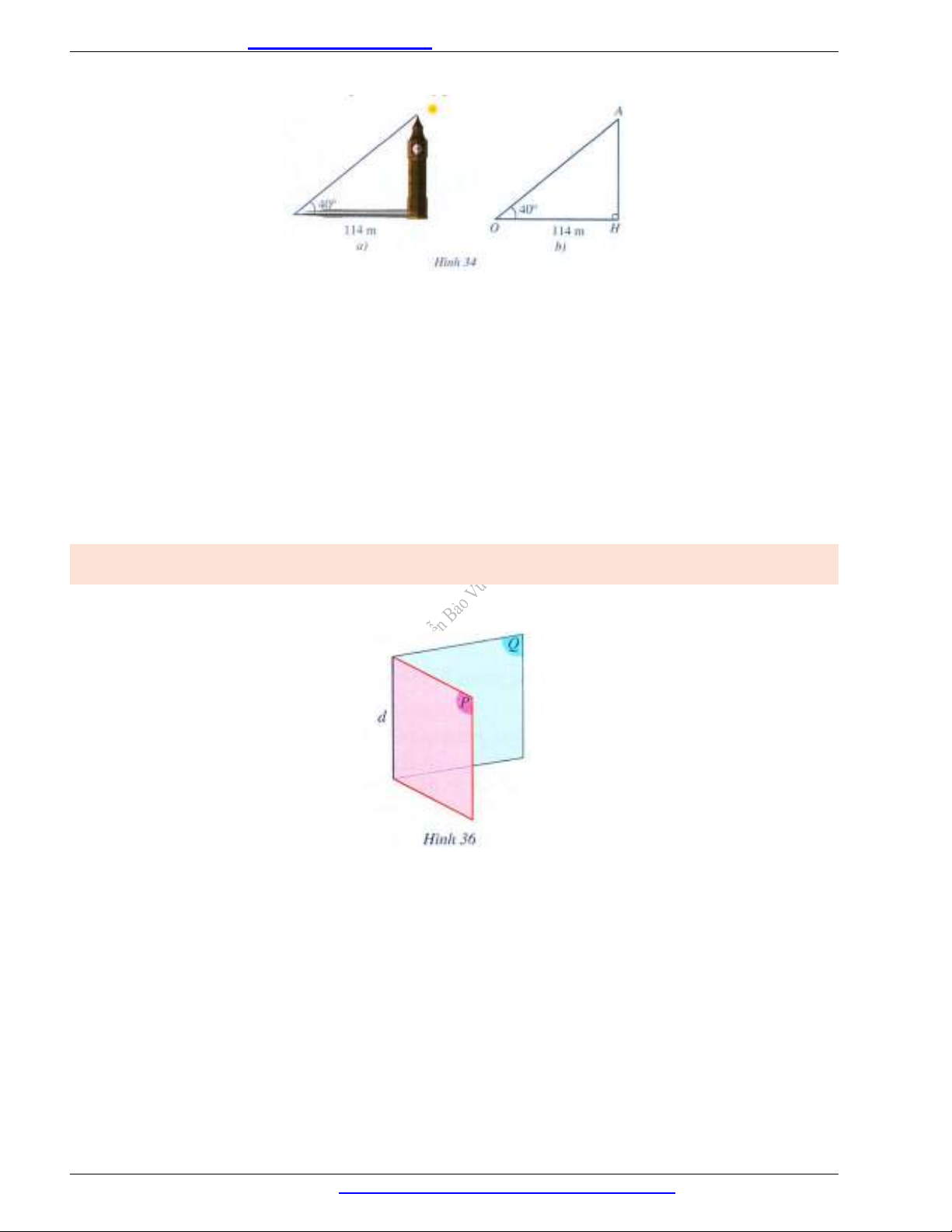
Ví dụ 2. Bài toán đo chiều cao của tháp khi không thể lên tới đỉnh tháp.
Để ước lượng chiều cao của tháp khi không thể lên tới đỉnh tháp, người ta đo góc giữa tia nắng chiếu qua
đỉnh tháp và mặt đất, đo chiều dài của bóng tháp trên mặt đất, từ đó ước lượng được chiều cao của tháp. Giả
BÀI 3. GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG. GÓC NHỊ DIỆN
•CHƯƠNG 8. QUAN HỆ VUÔNG GÓC
•|FanPage: Nguyễn Bảo Vương
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
sử khi tia nắng tạo với mặt đất một góc
40
, chiều dài của bóng tháp là
114 m
(Hình 34a). Tính chiều cao
của tháp theo đơn vị mét (làm tròn kết quả đến hàng phần mười).
Giải
Xét Hình 34b, độ dài
AH
chỉ chiều cao của tháp, độ dài
OH
chỉ chiều dài của bóng tháp, độ lớn của góc
AOH
chỉ số đo góc giữa tia nắng và mặt đất. Vì tam giác
OAH
vuông tại
H
nên
tan 114 tan 40 95,7( ).AH OH AOH m
II. GÓC NHỊ DIỆN
1. Khái niệm
Một đường thẳng nằm trong một mặt phẳng chia mặt phẳng đó thành hai phần, mỗi phần được gọi là một
nửa mặt phẳng và đường thẳng đó được gọi là bờ của mỗi nửa mặt phẳng này.
Khám phá kiến thức
Hai nửa mặt phẳng đó có chung bờ là đường thẳng chứa gáy sổ. Hình tạo bởi hai nủa mặt phẳng có chung
bờ đó là góc nhị diện.
Ta có khái niệm sau:
Kiến thức trọng tâm
Góc nhị diện là hình gồm hai nửa mặt phẳng có chung bờ.
Trong Hình 36, ta có góc nhị diện gồm hai nửa mặt phẳng
( )P
và
( )Q
có chung bờ là đường thẳng
d
, kí
hiệu là
[ , , ]P d Q
.
Đường thẳng
d
gọi là cạnh của góc nhị diện, mỗi nửa mặt phẳng
( )P
và
( )Q
gọi là một mặt của góc nhị
diện.
Chú ý: Góc nhị diện còn được kí hiệu là
[ , , ]M d N
với
,M N
lần lượt là các điểm thuộc các nửa mặt phẳng
( ),( )P Q
nhưng không thuộc đường thẳng
d
.
2. Số đo của góc nhị diện
Nhận xét
Điện thoại: 0946798489 TOÁN 11-CÁNH DIỀU
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
- Số đo góc phẳng nhị diện
xOy
không phụ thuộc vào vị trí của điểm
O
trên cạnh nhị diện và được gọi là số
đo của góc nhị diện đã cho.
- Số đo của góc nhị diện từ
0
đến
180
.
Trong trường hợp tổng quát, ta có định nghĩa sau:
Kiến thức trọng tâm
Trong không gian, cho góc nhị diện.
- Một góc có đỉnh thuộc cạnh của góc nhị diện, hai cạnh của góc đó lần lượt thuộc hai mặt nhị diện và cùng
vuông góc với cạnh của góc nhị diện, được gọi là góc phẳng nhị diện của góc nhị diện đã cho.
- Số đo của một góc phẳng nhị diện được gọi là số đo của góc nhị diện đó.
- Nếu số đo góc phẳng nhị diện bằng
90
thì góc nhị diện đó gọi là góc nhị diện vuông.
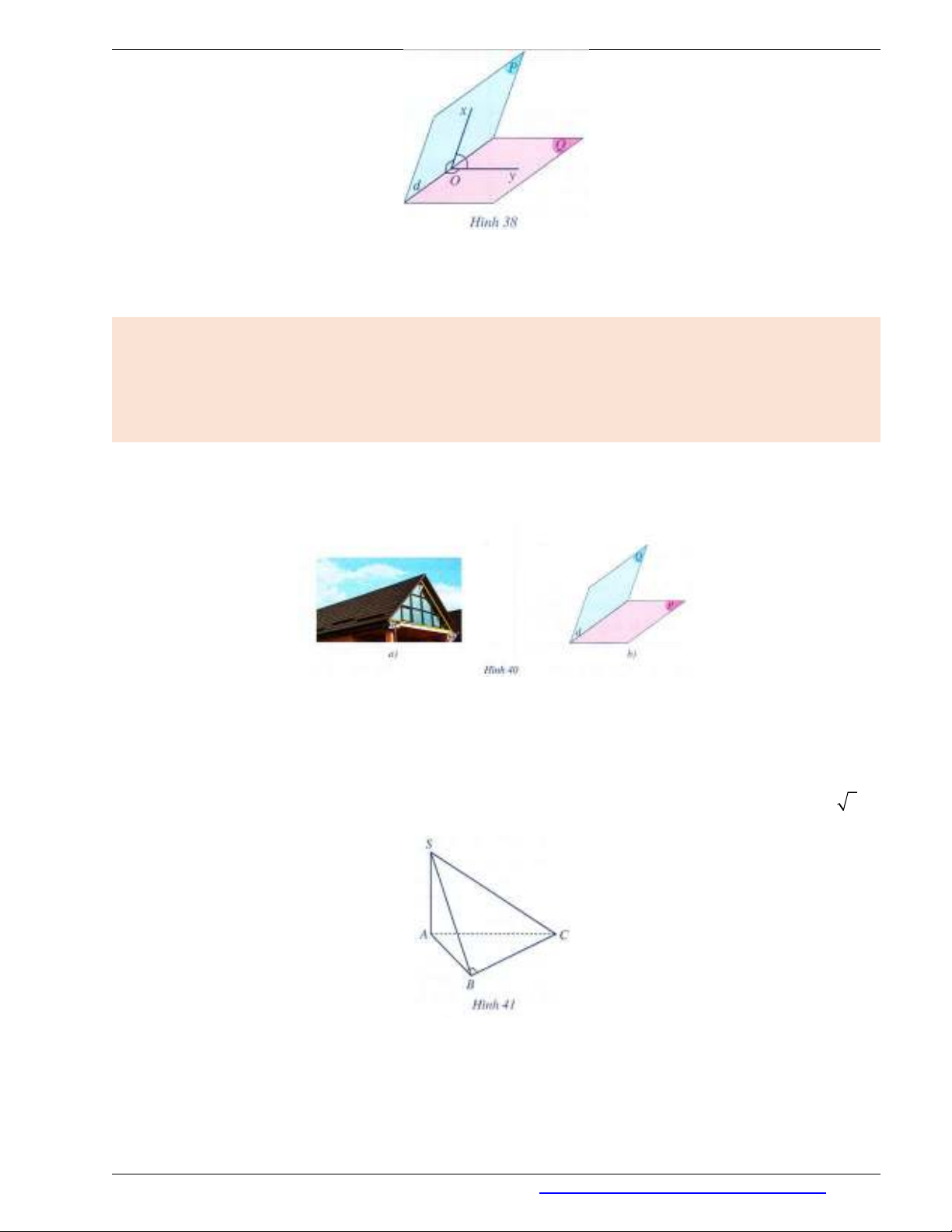
Ví dụ 4. Trong các công trình xây dựng nhà ở, độ dốc mái được hiểu là độ nghiêng của mái khi hoàn thiện
so với mặt phẳng nằm ngang. Khi thi công, mái nhà cần một độ nghiêng nhất định để đảm bảo thoát nước tốt
tránh gây ra tình trạng đọng nước hay thấm dột. Quan sát Hình 40 và cho biết góc nhị diện nào phản ánh độ
dốc của mái.
Giải
Giả sử nửa mặt phẳng
( )P
(minh hoạ mặt phẳng nằm ngang) và nửa mặt phẳng
( )Q
(minh hoạ mái nhà) cắt
nhau theo giao tuyến
d
(Hình 40b). Khi đó góc nhị diện có cạnh là đường thẳng
d
, hai mặt lần lượt là
( )P
và
( )Q
phản ánh độ dốc của mái. Độ dốc đó cũng được phản ánh bởi góc phẳng nhị diện
xOy
của góc nhị
diện trên (Hình 40a).
Ví dụ 5. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
, , ( ), 3B AB a SA ABC SA a
(Hình 41). Tính số đo của mỗi góc nhị diện sau:
a)
[ , , ]B SA C
;
b)
[ , , ]A BC S
.
Giải
a) Vì
( )SA ABC
nên
,SA AB SA AC
. Do đó, góc
BAC
là góc phẳng nhị diện của góc nhị diện
[ , , ]B SA C
. Do tam giác
ABC
vuông cân tại
B
nên
45BAC
. Vậy số đo của góc nhị diện
[ , , ]B SA C
bằng
45
.
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
b) Vì
( )SA ABC
nên
SA BC
. Mà
BC AB
nên
, suy ra
BC SB
. Do đó góc
SBA
là góc
phẳng nhị diện của góc nhị diện
[ , , ]A BC S
.
Trong tam giác vuông
SAB
, ta có:
3
tan 3.
SA a
SBA
AB a
Suy ra
60
SBA
. Vậy số đo của góc nhị diện
[ , , ]A BC S
bằng
60
.
PHẦN B. BÀI TẬP TỰ LUẬN (PHÂN DẠNG)
Dạng 1. Xác định góc giữa đường thẳng với mặt phẳng
Câu 1. Cho hình chóp
.
S ABC
có đáy là tam giác
ABC
đều cạnh bằng
3a
, các cạnh bên
, ,SA SB SC
bằng nhau và bằng
2 3a
. Tính góc giữa đường thẳng
SA
và mặt phẳng
( )ABC
.
Câu 2. Cho hình lăng trụ tam giác
ABC A B C
có đáy là tam giác
ABC
cân tại
A
, góc
BAC
bằng
120
và
2AB a
. Hình chiếu của
A
trên mặt phẳng
( )ABC
trùng với trung điểm
H
của
BC
, biết
2AA a
. Tính góc giữa đường thẳng
AA
và mặt phẳng
( )ABC
.
Câu 3. Cho tứ diện
ABCD
có tất cả các cạnh bằng nhau và bằng
a
. Tính côsin của góc giữa đường
thẳng
AB
và mặt phẳng
( )BCD
.
Câu 4. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
, ( )a SA ABCD
,
2SA a
.
a) Tính góc giữa đường thẳng
SC
và mặt phẳng
( )ABCD
.
b) Tính tang của góc giữa đường thẳng
SC
và mặt phẳng
( )SAB
.
Câu 5. Cho hình chóp
.
S ABC
có
( )SA ABC
, đáy là tam giác
ABC
vuông cân tại
B
, biết
, 6AB a SA a
.
a) Tính tang của góc giữa đường thẳng
SB
và mặt phẳng
( )SAC
.
b) Tính sin của góc giữa đường thẳng
AC
và mặt phẳng
( )SBC
.
Câu 6. Cho hình hộp
ABCD A B C D
có đáy
ABCD
là hình vuông cạnh a và
2AA a
, hình chiếu
vuông góc của
A
trên mặt phẳng
A B C D
trùng với trung điểm của
B D
. Tính góc giữa đường thẳng
AA
và mặt phẳng
A B C D
.
Câu 7. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông tâm
O
và các cạnh đều bằng
a
.
a) Chứng minh rằng
( )SO ABCD
.
b) Tính góc giữa đường thẳng
SA
và mặt phẳng
( )SBD
.
c) Gọi
M
là trung điểm của cạnh
SC
và
là góc giữa đường thẳng
OM
và mặt phẳng
( )SBC
. Tính
sin
.
Câu 8. Cho hình chóp .
S ABCD
có
( ), , 3SA ABCD AB AD SA AD a
,
AB a
. Tính số đo của:
a) Góc giữa đường thẳng
SB
và mặt phẳng
( )ABCD
.
b) Góc giữa đường thẳng
SD
và mặt phẳng
( )SAB
.
Dạng 2. Góc nhị diện
Câu 9. (SGK - Cánh diều 11 - Tập 2) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông và
( )SA ABCD
. Tính số đo của mỗi góc nhị diện sau:
a)
[ , , ]B SA D
;
b)
[ , , ]B SA C
.
Điện thoại: 0946798489 TOÁN 11-CÁNH DIỀU
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 10. (SGK - Cánh diều 11 - Tập 2) Cho hình chóp
.
S ABCD
có
( )SA ABCD
, đáy
ABCD
là hình
thoi cạnh
a
và
AC a
.
a) Tính số đo của góc nhị diện
[ , , ]B SA C
.
b) Tính số đo của góc nhị diện
[ , , ]B SA D
.
c) Biết
SA a
, tính số đo của góc giữa đường thẳng
SC
và mặt phẳng
( )ABCD
.
Câu 11. (SGK - Cánh diều 11 - Tập 2) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông, hai đường
thẳng
AC
và
BD
cắt nhau tại
, ( )O SO ABCD
, tam giác
SAC
là tam giác đều.
a) Tính số đo của góc giữa đường thẳng
SA
và mặt phẳng
( )ABCD
.
b) Chứng minh rằng
( )AC SBD
. Tính số đo của góc giữa đường thẳng
SA
và mặt phẳng
( )SBD
.
c) Gọi
M
là trung điểm của cạnh
AB
. Tính số đo của góc nhị diện
[ , , ]M SO D
.
Câu 12. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
a
,
( )SA ABCD
và
2
2
a
SA
. Tính số đo của góc nhị diện
[ , , ]S BD C
.
Câu 13. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh a, biết
( ) ( )SAB ABCD
,
( ) ( )SAD ABCD
và
SA a
. Tính côsin của số đo góc nhị diện
[ , , ]S BD C
và góc nhị diện
[ , , ]B SC D
.
Câu 14. Cho hình chóp
.
S ABC
có
3
( ), , 120 ,
2
a
SA ABC AB AC a BAC SA
. Tính số đo của góc
phẳng nhị diện
[ , , ]S BC A
Câu 15. Cho hình chóp
S ABCD
có
( )SA ABCD
, đáy
ABCD
là hình thoi cạnh
a
,
,
2
a
AC a SA
.
Gọi
O
là giao điểm của hai đường chéo hình thoi
ABCD
và
H
là hình chiếu của
O
trên
SC
. Tính số đo
các góc phẳng nhị diện:
a)
[ , , ]B SA D
;
b)
[ , , ]S BD A
;
c)
[ , , ]S BD C
;
d)
[ , , ]D SC B
.
Câu 16. Cho hình chóp tam giác đều
.
S ABC
, cạnh đáy bằng
a
, cạnh bên bằng
15
6
a
. Tính số đo góc
phẳng nhị diện
[ , , ]S BC A
.
Câu 17. Cho hình chóp
.
S ABC
có
( )SA ABC
. Tam giác
ABC
vuông tại
A
,
3
30 , ,
2
a
ABC AC a SA
. Tính số đo góc phẳng nhị diện
[ , , ]S BC A
.
Câu 18. Cho hình chóp .
S ABCD
có
( )SA ABCD
, đáy
ABCD
là hình thoi cạnh
a
và
AC a
. Tính số
đo của mỗi góc nhị diện sau:
a)
[ , , ]B SA C
;
b)
[ , , ]S DA B
.
Câu 19. Cho hình chóp .
S ABC
có
SA
(
ABC
),
, 3 , 4AB BC SA AB a BC a
. Gọi
, ,
lần lượt
là số đo của các góc nhị diện
[ , , ],[ , , ]B SA C A BC S
,
[ , , ]A SC B
. Tính:
a)
cos ,cos
;
b*)
cos
.