Trang 1
PHẦN A. LÝ THUYẾT VÀ VÍ DỤ MINH HỌA
I. GÓC LƯỢNG GIÁC
1. Góc hình học và số đo của chúng
Như chúng ta đã biết, góc (còn được gọi là góc hình học) là hình gồm hai tia chung gốc. Mỗi góc
có một số đo, đơn vị đo góc (hình học) là độ. Cụ thể như sau: Nếu ta chia đường tròn thành 360
cung tròn bằng nhau thì góc ở tâm chắn mỗi cung đó là 1
.
Số đo của một góc (hình học) không vượt quá
180
.
Một đơn vị khác được sử dụng nhiều khi đo góc là radian (đọc là ra-đi-an). Nếu trên đường tròn,
ta lấy một cung tròn có độ dài bằng bán kính thì góc ở tâm chắn cung đó gọi là góc có số đo 1
radian, gọi tắt là góc 1 radian. 1 radian còn viết tắt là 1 rad.
Nhận xét
Ta biết góc ở tâm có số đo
180
sẽ chắn cung bằng nửa đường tròn (có độ dài bằng
R
) nên số
đo góc
180
bằng
Rrad rad
R
.
Do đó,
0
180
1 57 17 45
rad

và
1 0,0175
180 rad rad
.
Chú ý: Người ta thường không viết chữ radian hay rad sau số đo của góc. Chẳng hạn,
2
rad cũng
được viết là
2
.
Ví dụ 1. Hãy hoàn thành bảng chuyển đổi số đo độ và số đo radian của một số góc đặc biệt sau.
Độ
30
?
60
?
120
?
180
Radian
?
4
?
2
?
3
4
?
Giải
Ta có bảng chuyển đổi số đo độ và số đo radian của một số góc đặc biệt.
Độ
30
45
60
90
120
135
180
Radian
6
4
3
2
2
3
3
4
2. Góc lượng giác và số đo của chúng
a) Khái niệm
Cho hai tia
,Ou Ov
. Nếu tia
Om
quay chỉ theo chiều dương (hay chỉ theo chiều âm) xuất phát từ
tia
Ou
đến trùng với tia
Ov
thì ta nói: Tia
Om
quét một góc luợng giác với tia đầu
Ou
và tia
cuối
Ov
, kí hiệu là
( , )Ou Ov
.
Ví dụ 2. Đọc tên góc lượng giác, tia đầu và tia cuối của góc lượng giác đó trong Hình
4a
.
BÀI 1. GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC
•CHƯƠNG 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
•|FanPage: Nguyễn Bảo Vương
Trang 2
Giải:
Trong Hình
4a
, góc lượng giác là
( , )Ox Oy
với tia đầu
Ox
tia đầu và tia cuối
Oy
.
Mỗi góc lượng giác gốc
O
được xác định bởi tia đầu
Ou
, tia cuối
Ov
và số đo của góc đó.
Ví dụ 3. Hãy biểu diễn trên mặt phẳng góc lượng giác trong mỗi trường hợp sau:
a) Góc lượng giác gốc
O
có tia đầu
Ou
, tia cuối
Ov
và có số đo
510
;
b) Góc lượng giác gốc
O
có tia đầu
Ou
, tia cuối
Ov
và có số đo
7
6
.
Giải
a) Ta có
510 360 150
. Góc lượng giác gốc
O
có tia đầu
Ou
, tia cuối
Ov
và có số đo
510
được biểu diễn ở Hình
6a
.
b) Ta có
7
6 6
. Góc lượng giác gốc
O
có tia đầu
Ou
, tia cuối
Ov
và có số đo
7
6
được biểu diễn ở Hình
6b
.
b) Tính chất
Cho hai góc lượng giác
( , ), ,Ou Ov O u O v
có tia đầu trùng nhau
Ou O u
, tia cuối trùng
nhau (
Ov O v
. Khi đó, nếu sử dụng đơn vị đo là độ thì ta có:
( , ) , 360Ou Ov O u O v k
với
k
là số nguyên
Nếu sử dụng đơn vị đo là radian thì công thức trên có thể viết như sau:
( , ) , 2Ou Ov O u O v k
với
k
là số nguyên.
Ví dụ 4. Cho góc lượng giác gốc
O
có tia đầu
Ou
, tia cuối
Ov
và có số đo
60
. Cho góc lượng
giác (
,O u O΄ ΄ ΄v΄
) có tia đầu
O u Ou
, tia cuối
O v Ov΄ ΄
. Viết công thức biểu thị số đo góc
lượng giác (
,O u O v΄ ΄ ΄ ΄
).
Giải
Ta có:
,O u O v΄ ΄ ΄ ΄
( , ) 360Ou Ov k
60 360 ( ).k k
Hệ thức Chasles về số đo của góc lượng giác
Với ba tia tuỳ ý
, ,Ou Ov Ow
, ta có:
( , ) ( , ) ( , ) 2 ( ).Ou Ov Ov Ow Ou Ow k k
Ví dụ 5. Cho góc lượng giác (
, )Ou Ov
có số đo là
3
4
, góc lượng giác
( , )Ou Ow
có số đo là
5
4
.
Tìm số đo của góc lượng giác
( , )Ov Ow
.
Giải
Theo hệ thức Chasles, ta có: 5
( , ) ( , ) ( , ) 2
5 3
2 2 ( ).
4 4 2
Ov Ow Ou Ow Ou Ov k
k k k
Trang 3
II. GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC
Trong mục này, ta sẽ mở rộng các giá trị lượng giác của góc hình học thành giá trị lượng giác của
góc lượng giác. Đó là cơ sở để xây dựng các hàm số lượng giác (biến số thực), những hàm số
quan trọng trong toán học, khoa học - kĩ thuật và trong thực tiễn.
1. Đường tròn lượng giác
Trong mặt phẳng toạ độ
Oxy
, ta quy ước: Chiều ngược chiều quay của kim đồng hồ là chiều
dương và chiều quay của kim đồng hồ là chiều âm. Như vậy, mặt phẳng toạ độ
Oxy
đã được định
hướng.
Trong mặt phẳng toạ độ đã được định hướng
Oxy
, lấy điểm
(1;0)A
. Đường tròn tâm
O
, bán kính
1OA
được gọi là đường tròn luợng giác (hay đường tròn đơn vị) gốc
A
.
Chú ý: Các điểm
(0;1), ( 1;0), (0; 1)B A B
nằm trên đường tròn lượng giác.
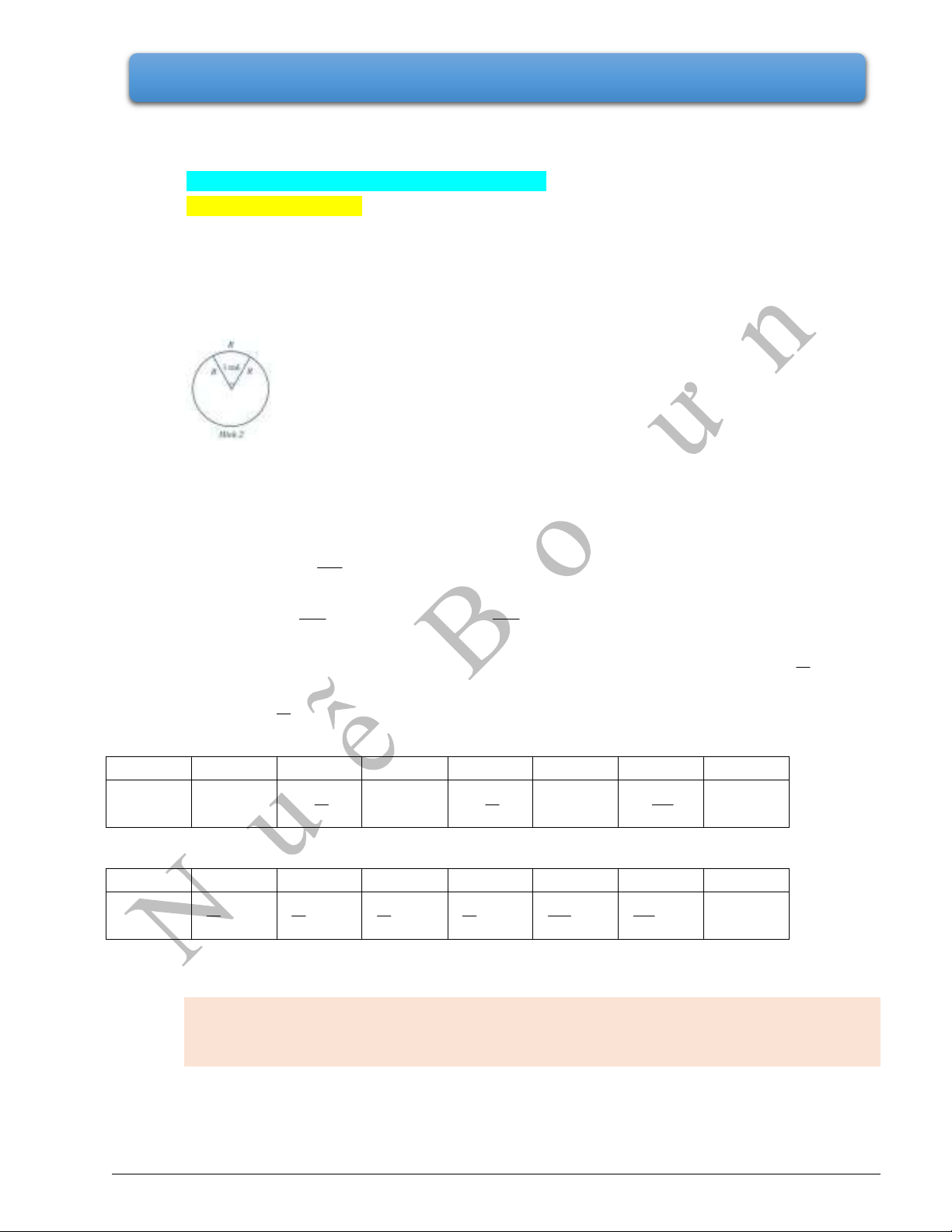
Ví dụ 6. Xác định điểm
M
trên đường tròn lượng giác sao cho
( , ) 135OA OM
.
Giải
Gọi
M
là điểm chính giữa của cung BA
trên đường tròn lượng giác.
Ta có:
( , ) 135OA OM
(Hình 9).
2. Giá trị lượng giác của góc lượng giác
Gọi toạ độ của điểm
M
trong hệ toạ độ
Oxy
là
( ; )x y
.
- Hoành độ
x
của điểm
M
gọi là côsin của góc lượng giác
và kí hiệu
cos ,cos x
.
- Tung độ
y
của điểm
M
gọi là sin của góc lượng giác
và kí hiệu
sin ,sin y
.
- Nếu
cos 0
thì tỉ số
sin
cos
gọi là tang của góc lượng giác
và kí hiệu
tan
,
sin
tan cos
.
- Nếu
sin 0
thì tỉ số
cos
sin
gọi là côtang của góc lượng giác
và kí hiệu
cot
,
cos
cot sin
.
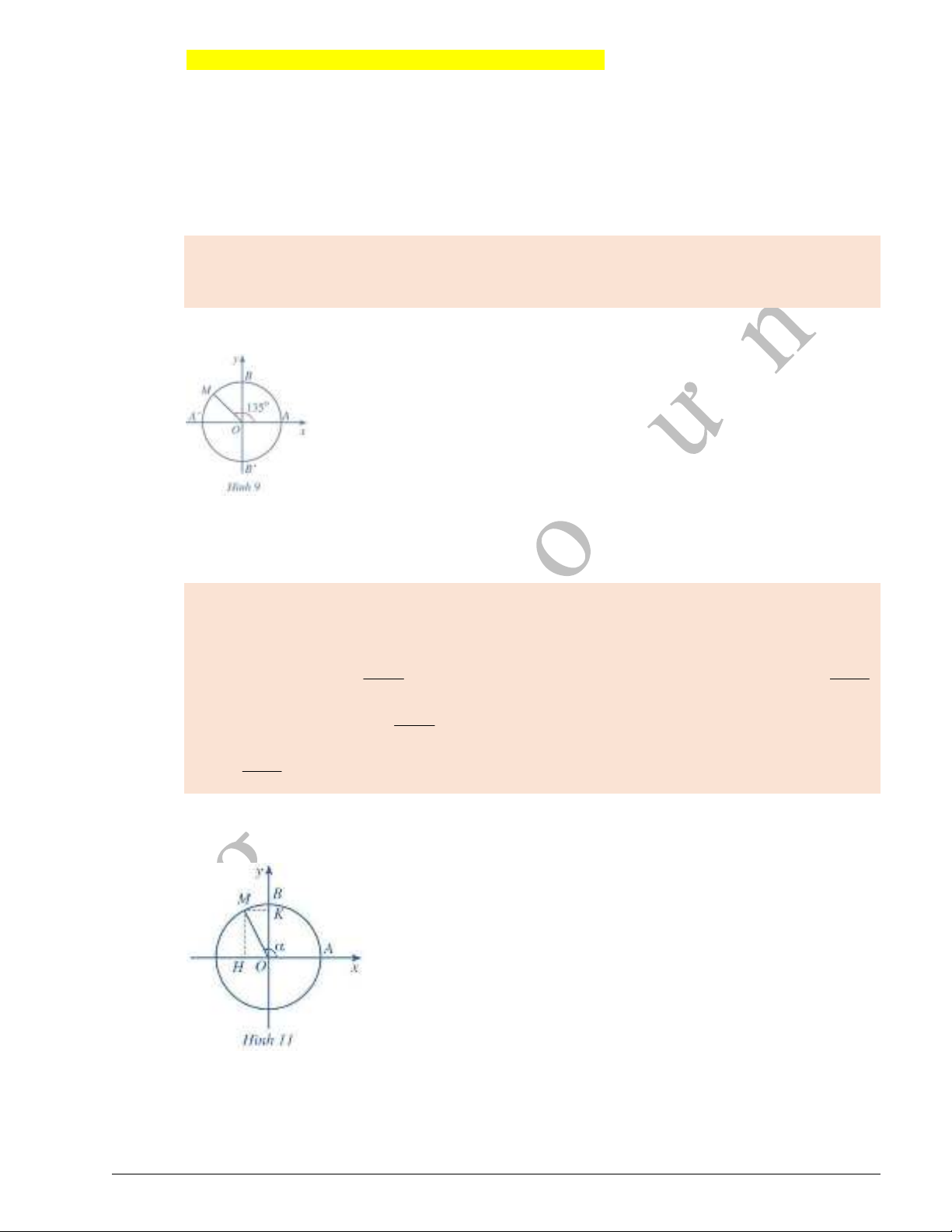
Ví dụ 7. Tìm các giá trị lượng giác của góc lượng giác
120
.
Giải
Lấy điểm
M
trên đường tròn lượng giác sao cho
( , ) 120OA OM
(Hình 11).
Gọi
,H K
lần lượt là hình chiếu của điểm
M
trên các trục
,Ox Oy
.
Khi đó, ta có:
120AOM
, suy ra
30BOM KOM
.
Theo hệ thức trong tam giác vuông
KOM
, ta có:
Trang 4
3 1
cos cos30 và sin sin30 .
2 2
1 3
;
2 2
OK OM KOM MK OM KOM
M
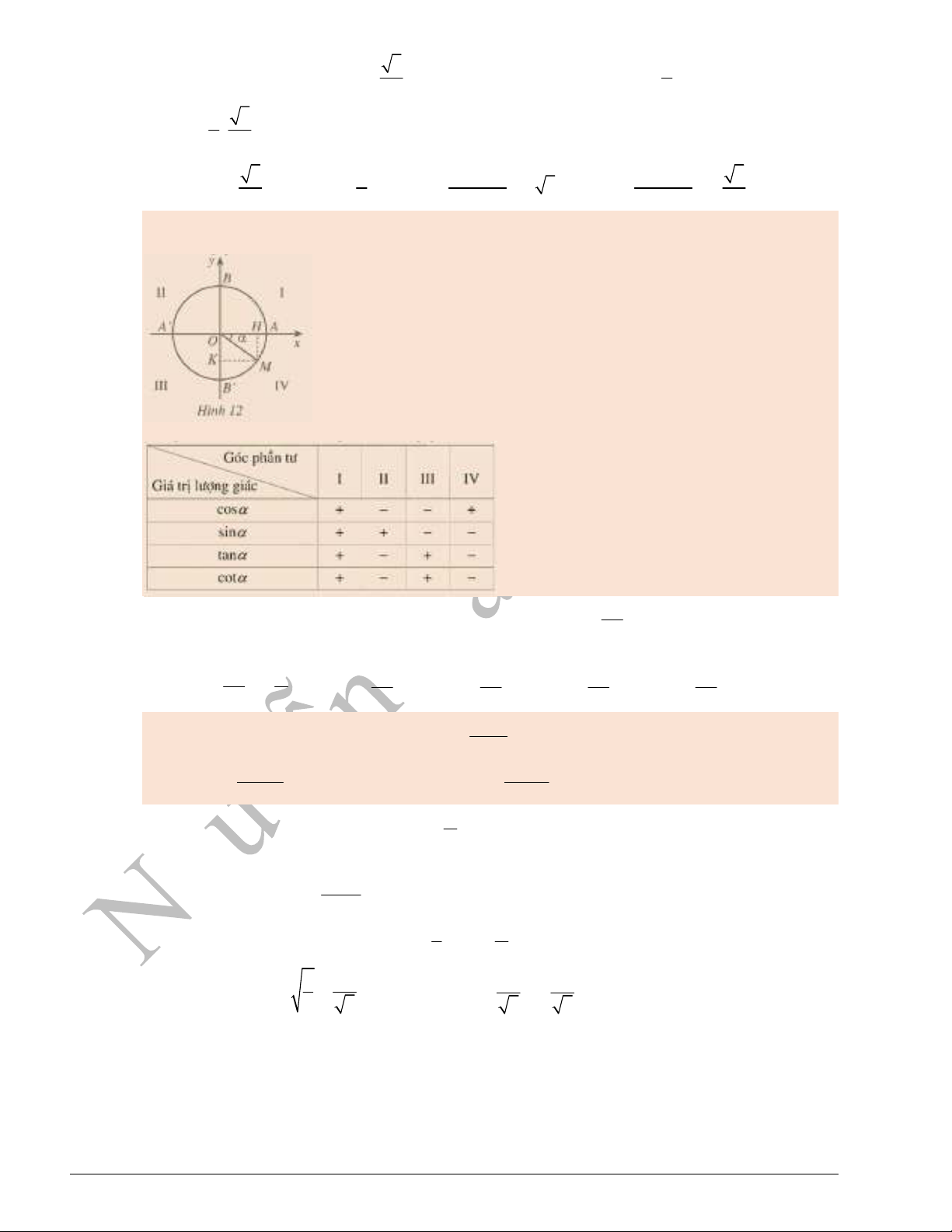
Dấu của các giá trị lượng giác của góc
( , )OA OM
phụ thuộc vào vị trí điểm
M
trên đường
tròn lượng giác (Hình 12).
Bảng xác định dấu của các giá trị lượng giác như sau:
Ví dụ 8. Xét dấu các giá trị lượng giác của góc lượng giác
3
4
.
Giải.
Do
3
4 2
nên
3 3 3 3
sin 0;cos 0; tan 0;cot 0
4 4 4 4
.
2 2
cos sin 1
với mọi
;
1
tan cot
với
cos 0,sin 0
;
2
2
1
1 tan cos
với
cos 0;
2
2
1
1 cot sin
với
sin 0
.
Ví dụ 9. Cho góc lượng giác
sao cho
0
2
và
tan 2
. Tính
cos ,sin
.
Giải
Do
tan 2
nên
sin 2
cos
, suy ra
sin 2cos
. Vì
2 2
cos sin 1
nên
2 2
cos ( 2cos ) 1
, suy ra
2
1
cos 5
. Do
0
2
nên
cos 0
.
Từ đó ta có:
1 1
cos 55
, suy ra
1 2
sin 2 5 5
.
Trang 5
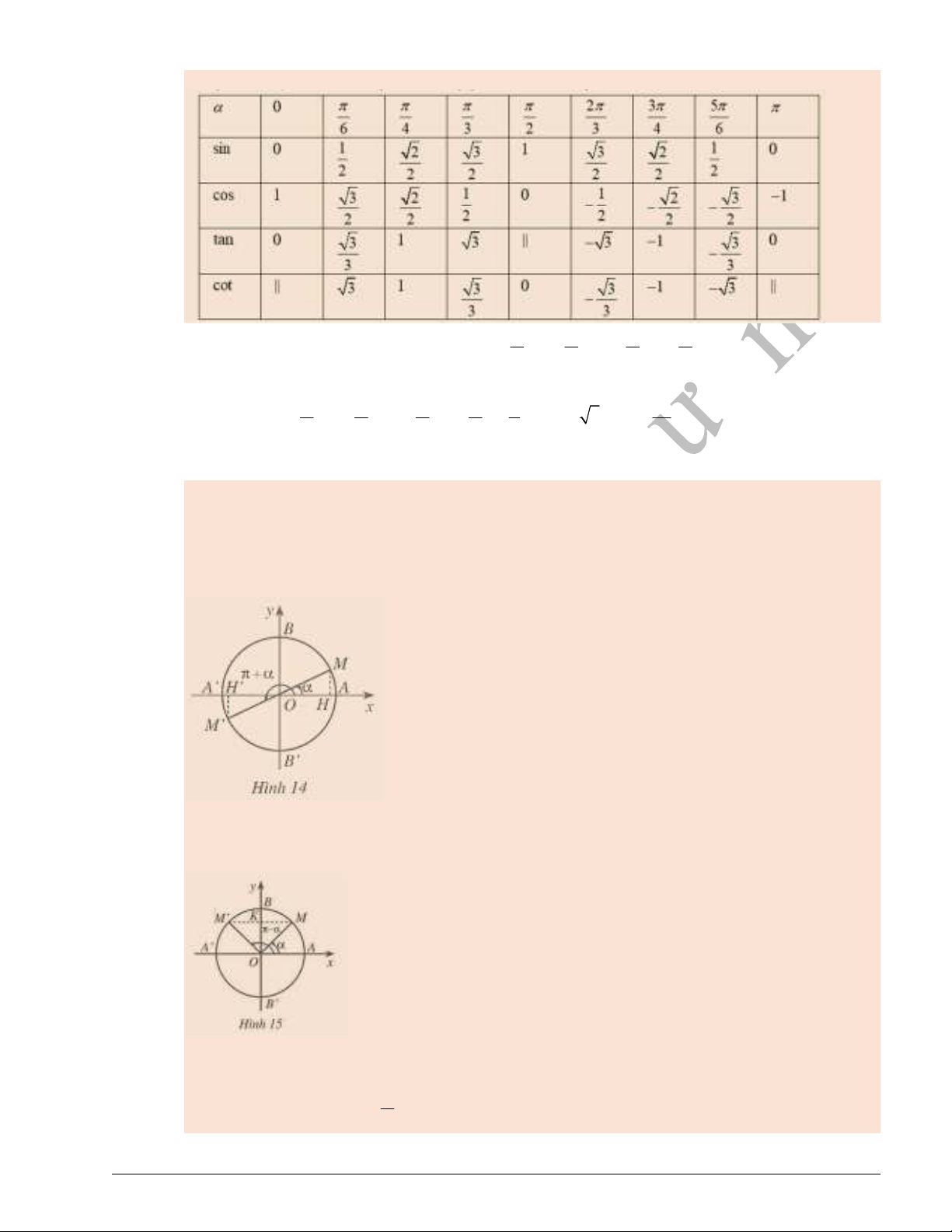
Bảng dưới đây nêu lên các giá trị lượng giác của một số góc đặc biệt.
Ví dụ 10. Tính giá trị của biểu thức:
2 2
cos tan cot sin
3 4 6 2
P
Giải
Ta có:
2
2 2 2
1 21
cos tan cot sin 1 ( 3) 1
3 4 6 2 2 4
P
.
3. Giá trị lượng giác của các góc có liên quan đặc biệt
Ta có các công thức sau cho hai góc đối nhau
(
và
)
:
sin( ) sin tan( ) tan
cos( ) cos cot( ) cot
Ta cũng có các công thức sau cho:
- Hai góc hơn kém nhau
(
và
)
(Hình 14):
sin( ) sin tan( ) tan
cos( ) cos cot( ) cot
- Hai góc bù nhau (
và
)
(Hình 15):
sin( ) sin tan( ) tan
cos( ) cos cot( ) cot
- Hai góc phụ nhau (
và
2
(Hình 16):