Trang 1
PHẦN A. LÝ THUYẾT VÀ VÍ DỤ MINH HỌA
I. HÀM SỐ MŨ
1. Định nghĩa
Nhận xét: Tương ứng mỗi giá trị
x
với giá trị
(1,062)
x
y
xác định một hàm số, hàm số đó gọi là
hàm số
hàm số mũ cơ số 1,062
.
Kiến thức trọng tâm
Cho số thực
( 0, 1)a a a
. Hàm số
x
y a
được gọi là hàm số mũ cơ số
a
.
Tập xác định của hàm số mũ
( 0, 1)
x
y a a a
là .
Ví dụ 1. Trong các hàm số sau, hàm số nào là hàm số mũ?
a)
2
y x
b)
( 3)
x
y
c)
1
yx
;
d)
5
y x
.
Giải
Trong các hàm số đã cho, chỉ có hàm số
( 3)
x
y
là có dạng
x
y a
với
3a
nên
( 3)
x
y
là
hàm số mũ.
Kiến thức trọng tâm
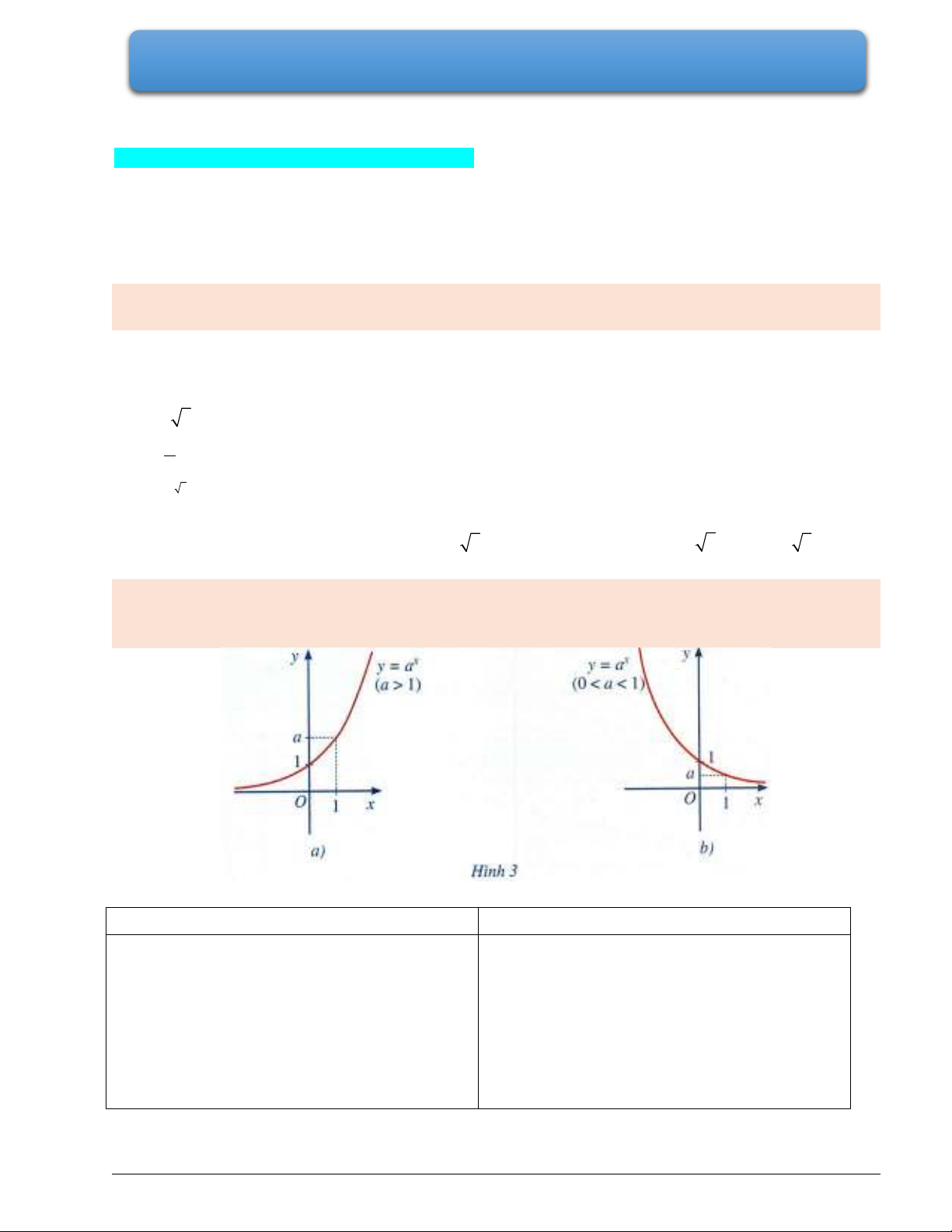
Đồ thị hàm số
( 0, 1)
x
y a a a
là một đường cong liền nét, cắt trục tung tại điểm có tung độ bằng
1 , nằm ở phía trên trục hoành và đi lên nếu
1a
, đi xuống nếu
0 1a
.
Nhận xét: Cho hàm số mũ
( 0, 1)
x
y a a a
.
( 1)
x
y a a
(0 1)
x
y a a
- Tập xác định:
; tập giá trị:
(0; )
.
- Tính liên tục
Hàm số
( 1)
x
y a a
là hàm số liên tục trên
.
- Giới hạn đặc biệt
lim 0, lim .
x x
x x
a a
 

- Sự biến thiên Hàm số đồng biến trên .
- Bảng biến thiên
- Tập xác định:
; tập giá trị:
(0; )
.
- Tính liên tục
Hàm số
(0 1)
x
y a a
là hàm số liên tục trên
.
- Giới hạn đặc biệt
lim , lim 0.
x x
x x
a a
 

- Sự biến thiên Hàm số nghịch biến trên .
- Bảng biến thiên
BÀI 3. HÀM SỐ MŨ - HÀM SỐ LOGARIT
•CHƯƠNG 6. LOGARIT
Trang 2
Chú ý: Từ tính liên tục và sự biến thiên của hàm số mũ, ta có thể chứng minh được mệnh đề sau:
Với mỗi
0N
, đường thẳng
y N
cắt đồ thị hàm số mũ
( 0, 1)
x
y a a a
tại một và chỉ một điểm
(Hình 4 minh hoạ trường hợp
1a
). Nói cách khác, ta có: Với mỗi
0N
, tồn tại duy nhất số thực
sao cho
a N
.
Ví dụ 2. Lập bảng biến thiên và vẽ đồ thị hàm số:
3 .
x
y
Giải
Vì hàm số
3
x
y
có cơ số
3 1
nên ta có bảng biến thiên như sau:
Đồ thị của hàm số
3
x
y
là một đường cong liền nét đi qua các điểm
1
1; , (0;1), (1;3), (2;9)
3
A B C D
(Hình 5).
Trang 3
Ví dụ 3. Trong Vật lí, sự phân rã của các chất phóng xạ được cho bởi công thức:
0
1
( ) 2
t
T
m t m
;
trong đó
0
m
là khối lượng chất phóng xạ ban đầu (tại thời điểm
0t
),
( )m t
là khối lượng chất
phóng xạ tại thời điểm
t
và T là chu kì bán rã (Nguồn: Giải tích 12, NXBGD Việt Nam, 2021). Hạt
nhân Poloni (Po) là chất phóng xạ
có chu kì bán rã là 138 ngày (Nguồn: Vật lí 12, NXBGD Việt
Nam, 2021). Giả sử lúc đầu có 100 gam Poloni. Tính khối lượng Poloni còn lại sau 100 ngày theo
đơn vị gam (làm tròn kết quả đến hàng phần mười).
Giải
Khối lượng Poloni còn lại sau 100 ngày là:
100
138
1
(100) 100 60,5( ).
2
m g
II. HÀM SỐ LÔGARIT
1. Định nghĩa
Ta có định nghĩa sau:
Kiến thức trọng tâm
Cho số thực
( 0, 1)a a a
. Hàm số
log
a
y x
được gọi là hàm số lôgarit cơ số
a
.
Tập xác định của hàm số lôgarit
log ( 0, 1)
a
y x a a
là
(0; )
.
Ví dụ 4. Trong các hàm số sau, hàm số nào là hàm số lôgarit?
a)
log 5
x
y
b)
log
x
y e
;
c)
5
logy x
d)
5
y x
.
Giải
Trong các hàm số đã cho, chỉ có hàm số
5
logy x
là có dạng hàm số lôgarit
log
a
y x
(với
5 0a
và
1a
).
Vậy hàm số
5
logy x
là hàm số lôgarit.
2. Đồ thị và tính chất
Khám phá kiến thức
Đồ thị hàm số
log ( 0, 1)
a
y x a a
là một đường cong liền nét, cắt trục hoành tại điểm có hoành độ
bằng 1 , nằm ở phía bên phải trục tung và đi lên nếu
1a
, đi xuống nếu
0 1a
.
Nhận xét: Cho hàm số lôgarit
log
a
y x
với
0, 1a a
.
log
a
y x
với
1a
log
a
y x
với
0 1a
- Tập xác định:
(0; )
; tập giá trị:
.
- Tính liên tục
Hàm số
log ( 1)
a
y x a
là hàm số liên tục
trên khoảng
(0; )
.
- Giới hạn đặc biệt
- Tập xác định:
(0; )
; tập giá trị:
.
- Tính liên tục
Hàm số
log (0 1)
a
y x a
là hàm số liên tục
trên khoảng
(0; )
.
- Giới hạn đặc biệt
Trang 4
0
lim log , lim log .
a a
x
x
x x

 
- Sự biến thiên
Hàm số đồng biến trên
(0; )
.
- Bảng biến thiên
0
lim log , lim log .
a a
x
x
x x

 
- Sự biến thiên
Hàm số nghịch biến trên
(0; )
.
- Bảng biến thiên
Ví dụ 5. Lập bảng biến thiên và vẽ đồ thị hàm số
3
log .y x
Giải
Vì hàm số
3
logy x
có cơ số
3 1
nên ta có bảng biến thiên như sau:
Đồ thị của hàm số
3
logy x
là một đường cong liền nét đi qua các điểm
1
; 1 , (1;0)
3
A B
,
(3;1), (9;2)C D
(Hình 9)
.
Ví dụ 6. Lốc xoáy là hiện tượng một luồng không khí xoáy tròn mở rộng ra từ một đám mây dông
xuống tới mặt đất (Hình 10). Các cơn lốc xoáy thường có sức tàn phá rất lớn. Tốc độ
S
(dặm/giờ)
của gió gần tâm của một cơn lốc xoáy được tính bởi công thức:
93log 65S d
, trong đó
d
(dặm)
là quãng đường cơn lốc xoáy di chuyển được.
(Nguồn: Ron Larson, Intermediate Algebra, Cengage)
Hãy tính tốc độ của gió ở gần tâm (làm tròn kết quả đến hàng đơn vị) khi cơn lốc xoáy di chuyển
được quãng đường là:
a) 5 dặm;
b) 10 dặm.
Trang 5
Giải
a) Tốc độ của gió ở gần tâm khi cơn lốc xoáy di chuyển được quãng đường 5 dặm là:
93log 5 65 130S
(dặm/giờ)
b) Tốc độ của gió ở gần tâm khi cơn lốc xoáy di chuyển được quãng đường 10 dặm là:
93log10 65 158S
(dặm/giờ)
PHẦN B. BÀI TẬP TỰ LUẬN (PHÂN DẠNG)
Dạng 1. Tính chất và đồ thị của hàm số mũ, hàm số lôgarit
Câu 1. (SGK - Cánh diều 11 - Tập 2) Lập bảng biến thiên và vẽ đồ thị hàm số
1
3
x
y
.
Câu 2.
(SGK - Cánh diều 11 - Tập 2) Lập bảng biến thiên và vẽ đồ thị hàm số
1
3
logy x
.
Câu 3. (SGK - Cánh diều 11 - Tập 2) Tìm tập xác định của các hàm số:
a)
12
x
y
;
b)
5
log (2 3)y x
;
c)
2
1
5
y x
.
Câu 4. (SGK - Cánh diều 11 - Tập 2) Trong các hàm số sau, hàm số nào đồng biến, hàm số nào
nghịch biến trên khoảng xác định của hàm số đó? Vì sao?
a)
3
2
x
y
;
b)
3
26
3
x
y
;
c)
logy x
d)
15
4
logy x
.
Câu 5. (SGK - Cánh diều 11 - Tập 2) Lập bảng biến thiên và vẽ đồ thị hàm số:
a)
4
x
y
;
b)
1
4
logy x
.
Câu 6. Lập bảng biến thiên và vẽ đồ thị hàm số:
a)
4
x
y
;
b)
1
4
logy x
.