intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Ôn tập Toán 11 sách Cánh diều - Chương 8-Bài 5: Khoảng cách

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:134

Thêm vào BST
Báo xấu
1
lượt xem 0
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

"Ôn tập Toán 11 sách Cánh diều - Chương 8-Bài 5: Khoảng cách" là tài liệu ôn tập quan trọng cho học sinh lớp 11. Bài ôn tập này trình bày tóm tắt các công thức tính khoảng cách từ một điểm đến đường thẳng, từ một điểm đến mặt phẳng và khoảng cách giữa hai đường thẳng song song, đi kèm bài tập trắc nghiệm và hướng dẫn giải chi tiết. Tài liệu này giúp học sinh vận dụng thành thạo các công thức khoảng cách trong không gian. Mời các bạn cùng tham khảo để làm bài tập hiệu quả.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Ôn tập Toán 11 sách Cánh diều - Chương 8-Bài 5: Khoảng cách

  1. TOÁN 11-CÁNH DIỀU Điện thoại: 0946798489 BÀI 5. KHOẢNG CÁCH • CHƯƠNG 8. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN • |FanPage: Nguyễn Bảo Vương PHẦN A. LÝ THUYẾT VÀ VÍ DỤ MINH HỌA I. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG THẲNG Ta đã biết khoảng cách từ một điểm đến một đường thẳng trong mặt phẳng. Trong không gian, khái niệm khoảng cách đó được định nghĩa tương tự như trong mặt phẳng. 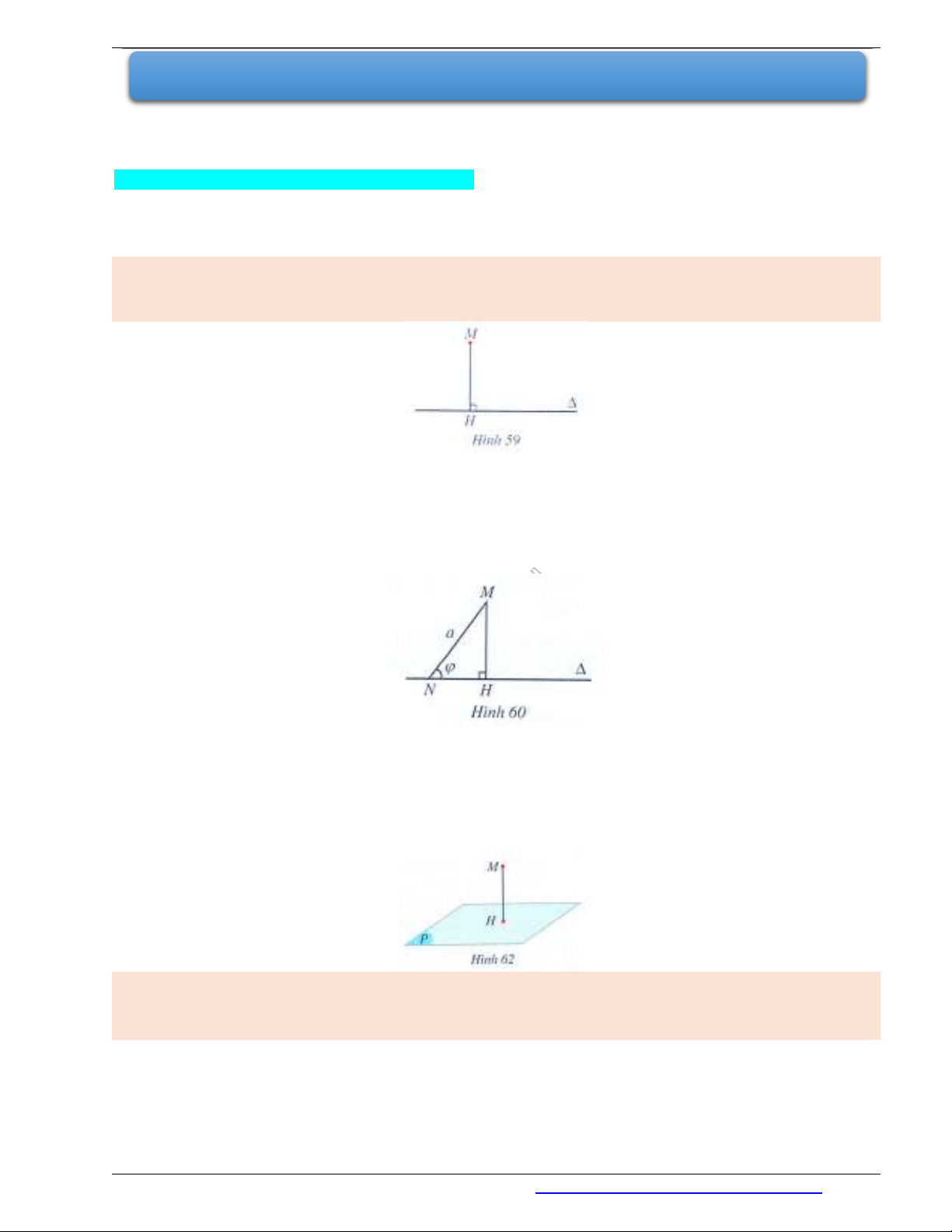Kiến thức trọng tâm Cho đường thẳng  và điểm M không thuộc  . Gọi H là hình chiếu của điểm M trên đường thẳng  . Độ dài đoạn thẳng MH gọi là khoảng cách từ điểm M đến đường thẳng  , kí hiệu d (M , ) . Trong Hình 59, ta có d (M , )  MH . Chú ý: Khi điểm M thuộc đường thẳng  thì d (M , )  0 . Ví dụ 1. Cho đoạn thẳng MN có độ dài a và đường thẳng  đi qua N sao cho góc giữa hai đường thẳng MN và  là   0    90  . Tính khoảng cách từ M đến  theo a, . Giải. (Hình 60) Gọi H là hình chiếu của M trên đường thẳng  . Khi đó d (M , )  MH . Vì góc giữa hai đường thẳng  MN và  là  nên MNH   . Suy ra MH  MN . sin   a sin  . Vậy d (M , )  a sin  . II. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG Ta có định nghĩa sau (Hình 62): Kiến thức trọng tâm Cho mặt phẳng ( P) và điểm M không thuộc mặt phẳng ( P) . Gọi H là hình chiếu của M trên mặt phẳng ( P) . Độ dài đoạn thẳng MH gọi là khoảng cách từ điểm M đến mặt phẳng ( P) , kí hiệu d (M ,( P)) . Chú ý: Khi điểm M thuộc mặt phẳng ( P) thì d (M , ( P))  0 . Ví dụ 2. Cho hình chóp S . ABCD có đáy ABCD là hình vuông cạnh a, O là giao điểm của AC và BD, SO  ( ABCD) , SO  a . Tính: a) Khoảng cách từ điểm S đến mặt phẳng ( ABCD) ; b) Khoảng cách từ điểm B đến mặt phẳng (SAC ) . Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
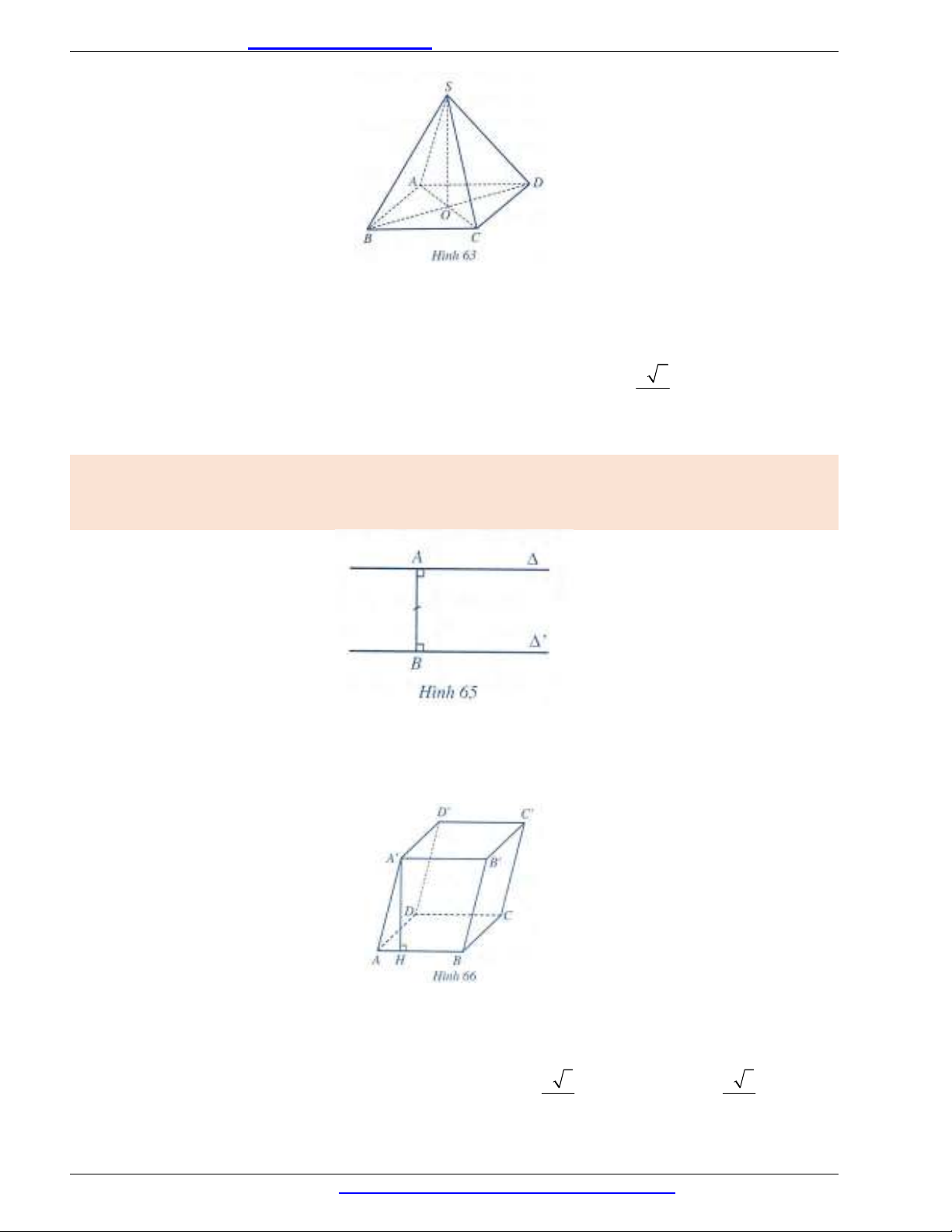
  2. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ Giải. (Hình 63) a) Ta có: O  ( ABCD), SO  ( ABCD) . Suy ra khoảng cách từ điểm S đến mặt phẳng ( ABCD) là SO  a . b) Do SO  ( ABCD), BO  ( ABCD) nên SO  BO . Vì BO vuông góc với hai đường thẳng AC và SO cắt nhau trong (SAC ) nên BO  (SAC ) . Do a 2 O  (SAC ), BO  ( SAC ) nên khoảng cách từ B đến mặt phẳng (SAC ) là BO  . 2 III. KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG SONG SONG Ta có định nghĩa sau: Kiến thức trọng tâm Khoảng cách giữa hai đường thẳng song song  ,   là khoảng cách từ một điểm bất kì thuộc đường thẳng này đến đường thẳng kia, kí hiệu d  ,   . Trong Hình 65, ta có d  ,     AB với A  , B   , AB  , AB   và  / /  . Ví dụ 3. Cho hình hộp ABCD  A BC  D ' có AA  a , góc giữa hai đường thẳng AB và DD  bằng 60 . Tính khoảng cách giữa hai đường thẳng AB và A B  . Giải. (Hình 66) Gọi H là hình chiếu vuông góc của A trên AB . Do AB / / A B nên d  AB, A B    A H . Vì AA / / DD nên góc giữa đường thẳng AB và AA bằng góc giữa đường thẳng AB và DD  . Suy ra   60 . A AH Trong tam giác vuông HAA có A H  AA  sin   a sin 60  a 3 a 3 A AH . Vậy d  AB, A B   . 2 2 IV. KHOẢNG CÁCH GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG Ta có định nghĩa sau: Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
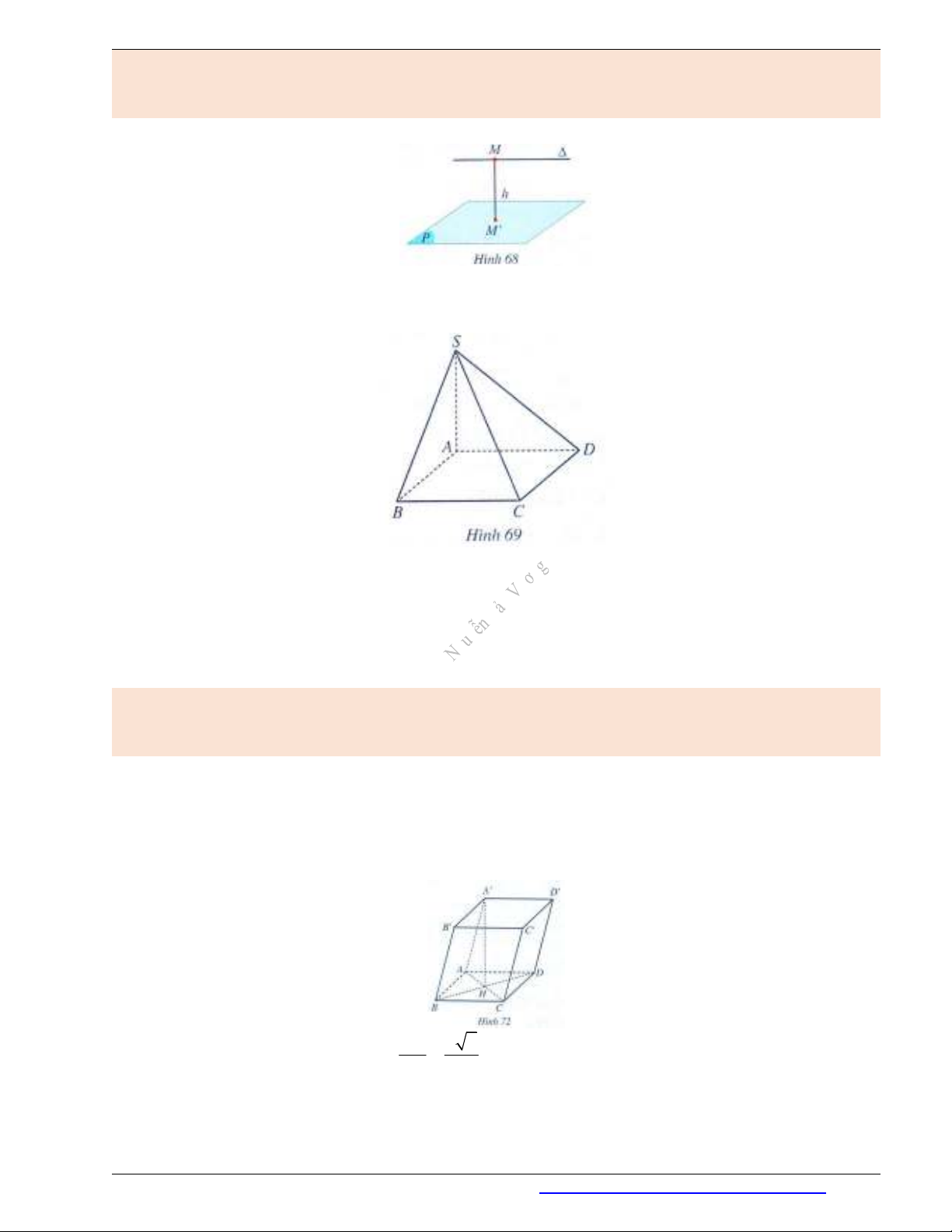
  3. Điện thoại: 0946798489 TOÁN 11-CÁNH DIỀU Kiến thức trọng tâm Cho đường thẳng  song song với mặt phẳng ( P) . Khoảng cách giữa đường thẳng  và mặt phẳng ( P) là khoảng cách từ một điểm bất kì thuộc đường thẳng  đến mặt phẳng ( P) , kí hiệu d (,( P)) . Trong Hình 68, ta có: d (, ( P))  MM   h , trong đó M   , M   ( P), MM   ( P ) và  / /( P) . Ví dụ 4. Cho hình chóp S . ABCD có đáy ABCD là hình vuông cạnh a, SA  ( ABCD) . Chứng minh CD / /(SAB) và tính khoảng cách giữa CD và mặt phẳng (SAB) . Giải. (Hình 69) Do CD / / AB, AB  ( SAB), CD  (SAB) nên CD / /(SAB) . Vì D  CD nên d (CD,(SAB))  d ( D,(SAB)) .  Do SA  ( ABCD), DA  ( ABCD) nên SA  DA . Vì DA vuông góc với hai đường thẳng AB, SA cắt nhau trong (SAB) nên DA  (SAB) . Do đó d ( D, (SAB))  DA  a . Vậy d (CD, (SAB))  a . V. KHOẢNG CÁCH GIỮA HAI MẶT PHẲNG SONG SONG Ta có định nghĩa sau: Kiến thức trọng tâm Khoảng cách giữa hai mặt phẳng song song ( P),(Q) là khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia, kí kiệu d (( P), (Q)) . Trong Hình 71, ta có: d (( P), (Q))  IK  h với I  ( P) , K  (Q), IK  ( P), IK  (Q) và ( P) / /(Q) . Ví dụ 5. Cho hình hộp ABCD  A BC  D có tất cả các cạnh bằng a và đáy là hình vuông. Hình chiếu của A trên mặt phẳng ( ABCD) là giao điểm H của AC và BD . Tính khoảng cách giữa hai mặt phẳng ( ABCD) và  A BC  D  . Giải. (Hình 72) AC a 2 Vì H là trung điểm của AC nên AH   . 2 2 Do A H  ( ABCD ) và AH  ( ABCD) nên A H  AH . Xét tam giác AA H vuông tại H có: Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
  4. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ 2  2  2 a 2 2 a2 2  a 2 A H  A A  AH  a     . Suy ra A H   2  .   2 2 a 2 Vậy khoảng cách giữa hai mặt phẳng ( ABCD) và ( A BC  D  bằng A H  . 2 VI. KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU Từ đó, ta có định nghĩa sau: Kiến thức trọng tâm Cho hai đường thẳng a, b chéo nhau. - Đường thẳng c vừa vuông góc, vừa cắt cả hai đường thẳng a và b được gọi là đường vuông góc chung của hai đường thẳng đó. - Đoạn thẳng có hai đầu mút là giao điểm của đường thẳng c với hai đường thẳng a, b được gọi là đoạn vuông góc chung của hai đường thẳng đó. - Độ dài đoạn vuông góc chung của hai đường thẳng a, b gọi là khoảng cách giữa hai đường thẳng đó, kí hiệu d (a, b) . 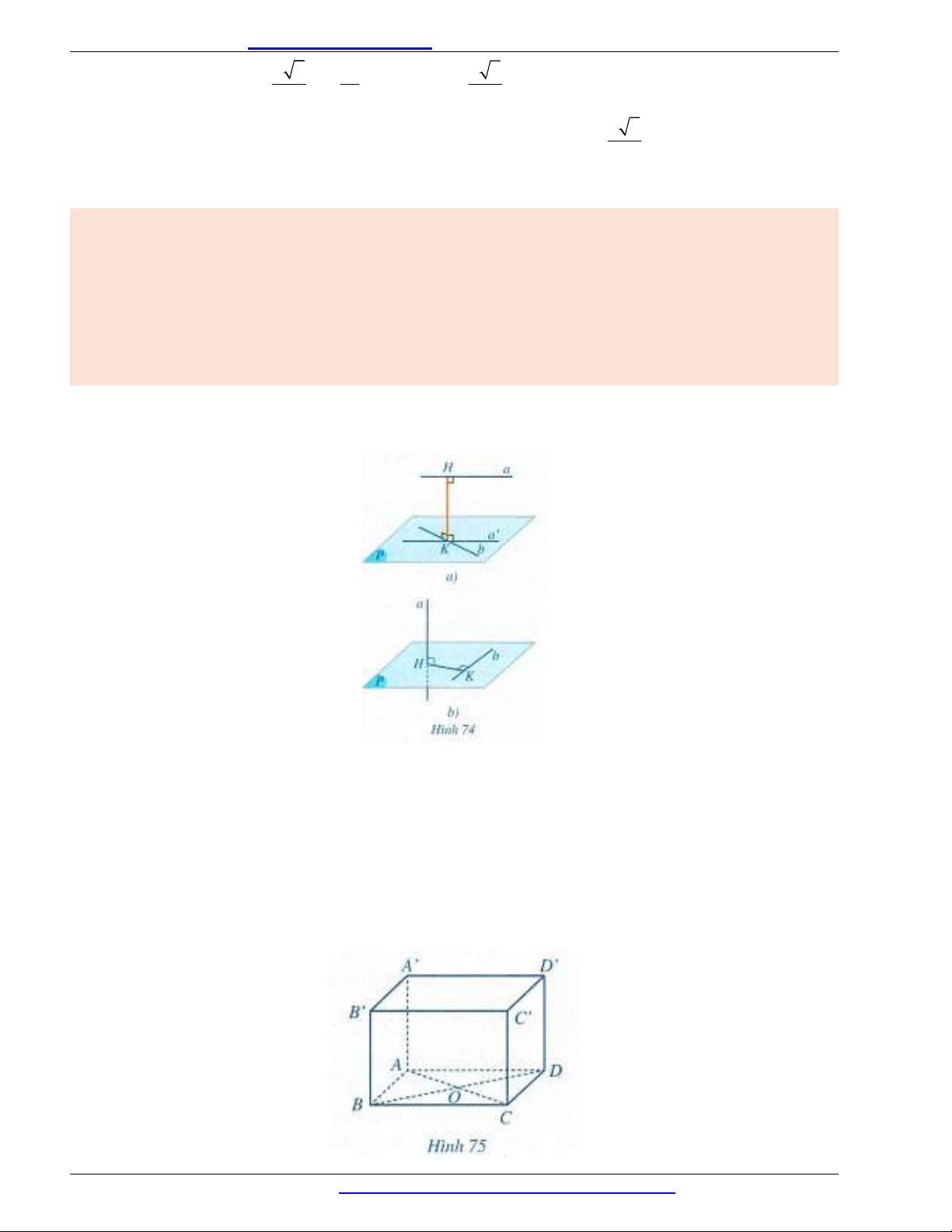Nhận xét: Gọi mặt phẳng chứa b và song song với a là ( P ) , hình chiếu của a trên ( P) là a , giao điểm của a và b là K , hình chiếu của K trên a là H . Khi đó, HK là đoạn vuông góc chung của hai đường thẳng chéo nhau a, b (Hình 74a). Ngoài ra, ta cũng có d (a, b)  d (a,( P)) . Khi a  b , ta có thể làm như sau: Gọi mặt phẳng đi qua b và vuông góc với a là ( P ) , giao điểm của a và ( P) là H , hình chiếu của H trên b là K . Khi đó HK là đoạn vuông góc chung của hai đường thẳng chéo nhau a, b (Hình 74b). Ví dụ 6. Cho lăng trụ ABCD  A BC  D có đáy ABCD là hình vuông cạnh 2a, O là giao điểm của AC và BD, AA  a , AA vuông góc với mặt phẳng chứa đáy. Tính: a) d  AC , A B   ; b) d  CC  , BD  . Giải. (Hình 75) Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  5. Điện thoại: 0946798489 TOÁN 11-CÁNH DIỀU a) Vì AA vuông góc với cả hai mặt phẳng ( ABCD) và  A B C D       nên AA  AC , AA  A B . Suy ra đoạn  thẳng AA là đoạn vuông góc chung của AC và A B  . Vậy d  AC , A B   AA  a . b) Vì CC vuông góc với ( ABCD) nên CC   OC . Do đáy ABCD là hình vuông có O là giao điểm của AC và BD nên BD  OC . Suy ra đoạn thẳng OC là đoạn vuông góc chung của CC và BD .   Vậy d CC  , BD  OC  a 2 . PHẦN B. BÀI TẬP TỰ LUẬN (PHÂN DẠNG) Dạng 1. Tính khoảng cách Câu 1. (SGK - Cánh diều 11 - Tập 2) Cho hình chóp S . ABC có SA  ( ABC ), AI  BC ( I  BC ), AH  SI ( H  SI ) . Chứng minh rằng khoảng cách từ A đến mặt phẳng (SBC ) bằng AH . Câu 2. (SGK - Cánh diều 11 - Tập 2) Cho hình chóp S . ABC có SA  a , góc giữa SA và mp( ABC ) là 60 . Gọi M , N lần lượt là trung điểm của cạnh SA và SB . Chứng minh MN / /( ABC ) và tính d (MN ,( ABC )) . Câu 3. (SGK - Cánh diều 11 - Tập 2) Cho hình lăng trụ ABC.A BC  ' có cạnh bên bằng a , góc giữa đường thẳng AA và mặt phẳng ( ABC ) bằng 60 . Tính khoảng cách giữa hai mặt phẳng ( ABC ) và ABC .    Câu 4. (SGK - Cánh diều 11 - Tập 2) Cho hình chóp tam giác S . ABC có đáy ABC là tam giác đều cạnh a, SA  ( ABC ) . Tính d (SA, BC ) . 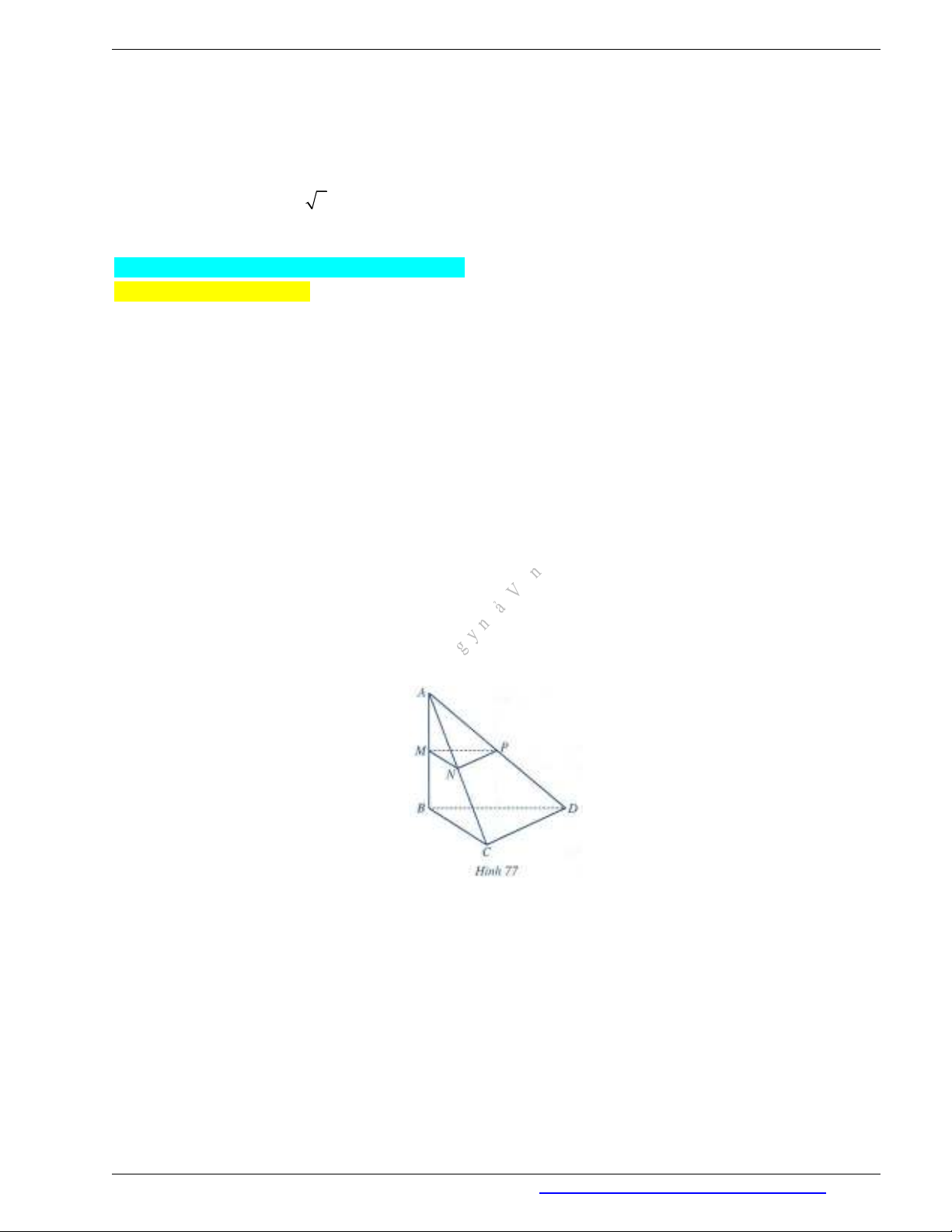Câu 5. (SGK - Cánh diều 11 - Tập 2) Cho hình tứ diện ABCD có AB  a, BC  b, BD  c ,     BCD  90 . Gọi M , N , P lần lượt là trung điểm của AB, AC, AD (Hình 77). ABC ABD  a) Tính khoảng cách từ điểm C đến đường thẳng AB . b) Tính khoảng cách từ điểm D đến mặt phẳng ( ABC ) . c) Tính khoảng cách giữa hai đường thẳng AB và CD . Câu 6. (SGK - Cánh diều 11 - Tập 2) Với giả thiết ở Bài tập 2, hãy: a) Chứng minh rằng MN / / BC . Tính khoảng cách giữa hai đường thẳng MN và BC . b) Chứng minh rằng MP / /( BCD) . Tính khoảng cách từ đường thẳng MP đến mặt phẳng ( BCD) . c) Chứng minh rằng (MNP) / /( BCD) . Tính khoảng cách giữa hai mặt phẳng ( MNP) và ( BCD) . Câu 7. (SGK - Cánh diều 11 - Tập 2) Cho hình chóp S . ABCD có SA  ( ABCD) , đáy ABCD là hình vuông cạnh a, SA  a (Hình 78). Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
  6. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ a) Tính khoảng cách từ điểm S đến đường thẳng CD . b) Tính khoảng cách từ điểm D đến mặt phẳng (SAB) . c) Tính khoảng cách từ điểm A đến mặt phẳng ( SCD) . Câu 8. (SGK - Cánh diều 11 - Tập 2) Với giả thiết ở Bài tập 4, hãy: a) Chứng minh rằng BC / /(SAD) và tính khoảng cách giữa BC và mặt phẳng (SAD) . b) Chứng minh rằng BD  (SAC ) và tính khoảng cách giữa hai đường thẳng BD và SC . Câu 9. Cho hình chóp S . ABC có SA  ( ABC ) , đáy là tam giác ABC vuông tại B , biết SA  AB  BC  a . Tính theo a khoảng cách: a) Từ điểm B đến đường thẳng SC . b) Từ điểm A đến mặt phẳng (SBC) . c) Giữa hai đường thẳng chéo nhau AB và SC . Câu 10. Cho hình lập phương ABCD  A BC  D có cạnh bằng a . Tính theo a khoảng cách: a) Từ điểm A đến mặt phẳng  BDA  . b) Giữa hai đường thẳng song song BC và A D . c) Giữa hai đường thẳng chéo nhau A B và BC . Câu 11. Cho hình lập phương ABCD  A BC  D có cạnh bằng a . Tính theo a khoảng cách: a) Giữa hai đường thẳng AB và C  D . b) Giữa đường thẳng AC và mặt phẳng  A B C  D   . c) Từ điểm A đến đường thẳng B D . d) Giữa hai đường thẳng AC và B D . Câu 12. Cho hình chóp S . ABC có đáy là tam giác ABC đều cạnh bằng a, SA  ( ABC ) và SA  2 a . Tính theo a khoảng cách: a) Từ điểm B đến mặt phẳng (SAC) . b) Từ điểm A đến mặt phẳng (SBC) . c) Giữa hai đường thẳng AB và SC . Câu 13. Cho hình chóp S . ABC có đáy ABC là tam giác vuông tại A , góc ABC bằng 60 , biết tam giác SBC đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng ( ABC ) . Tính theo a khoảng cách: a) Từ điểm S đến mặt phẳng ( ABC ) . b) Từ điểm B đến mặt phẳng (SAC) . c) Giữa hai đường thẳng AB và SC . Câu 14. Cho hình hộp chữ nhật ABCD  A BC  D có AB  a, AD  a 2, AA  a 3 . Tính theo a khoảng cách: Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  7. Điện thoại: 0946798489 TOÁN 11-CÁNH DIỀU a) Từ điểm A đến mặt phẳng  BDD  B   . b) Giữa hai đường thẳng BD và CD . Câu 15. Cho hình lăng trụ đứng ABC  A BC  có đáy ABC là tam giác vuông tại A và AB  AC  AA  a . Tính theo a khoảng cách: a) Từ điểm A đến đường thẳng BC  . b) Giữa hai đường thẳng BC và AB . Câu 16. Cho điểm A nằm ngoài đường thẳng  , hai điểm B, C thuộc  sao cho BC  a , diện tích tam giác ABC bằng S . Tính khoảng cách từ điểm A đến đường thẳng  theo a, S . Câu 17. Cho hình chóp S. ABC có mặt phẳng ( SAB ) vuông góc với mặt đáy, tam giác SAB vuông 3a tại S , AB  a, SA  . Tính khoảng cách từ điểm S đến mặt phẳng ( ABC ) . 5 Câu 18. Cho hình thang cân ABCD có AB / / CD, AB  6a, CD  14a, AD  BC  5a . a) Gọi H , K lần lượt là hình chiếu của A, B trên CD . Tính độ dài các đoạn thẳng HK , DH , CK . b) Tính khoảng cách giữa hai đường thẳng AB và CD . Câu 19. Cho hình chóp S . ABCD có ABCD là hình chữ nhật, SAB là tam giác đều, ( SAB )  ( ABCD ), AB  a, AD  2a . a) Chứng minh rằng CD / /( SAB ) . Tính khoảng cách giữa CD và mặt phẳng ( SAB ) . b) Chứng minh rằng BC / /( SAD ) . Tính khoảng cách giữa BC và mặt phẳng ( SAD) . Câu 20. Cho hình lăng trụ ABC . A B C  ' có  A ABB   ( ABC ), AA  2a,   60 . Tính khoảng cách giữa hai mặt phẳng ( ABC ) và  A B C  .     A AB     Câu 21. Cho hình hộp chữ nhật ABCD  A B C  D  có AB  a, AD  3a, AA  2a . Tính khoảng cách giữa hai đường thẳng: a) AB và B C  ; b) AA và BC ; c) BB  và C  D . Câu 22. Cho hình chóp S. ABC có SA  ( ABC ), AB  BC , SA  AB  3a, BC  4a . Tính khoảng cách: a) Từ điểm C đến mặt phẳng ( SAB ) ; b) Giữa hai đường thẳng SA và BC ; c) Từ điểm A đến mặt phẳng ( SBC ) ; d) Từ điểm B đến mặt phẳng ( SAC ) ; e*) Giữa hai đường thẳng AB và SC . Câu 23. Cho hình chóp S . ABCD có ABCD là hình chữ nhật, AB  2a, AD  3a , tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với ( ABCD ) . Tính khoảng cách: a) Từ điểm C đến mặt phẳng ( SAB ) ; b) Giữa hai đường thẳng SB và CD ; c) Giữa hai đường thẳng BC và SA ; d) Từ điểm S đến mặt phẳng ( ABCD ) . Câu 24. Cho hình chóp S . ABCD có ABCD là hình vuông cạnh a , AC cắt BD tại O , SO  ( ABCD ), SA  2a . Tính khoảng cách: Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
  8. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ a) Từ điểm A đến mặt phẳng ( SBD) ; b) Giữa hai đường thẳng SO và CD ; c) Từ điểm O đến mặt phẳng ( SCD ) ; d*) Giữa hai đường thẳng AB và SD . Câu 25. Cho hình hộp ABCD  A BC  D có ABCD là hình thoi cạnh a, AA  ( ABCD) , AA  2a, AC  a . Tính khoảng cách: a) Từ điểm A đến mặt phẳng  BCC  B  ; b) Giữa hai mặt phẳng  ABB A  và  CDDC   ; c*) Giữa hai đường thẳng BD và AC . Câu 26. Cho hình chóp S . ABC có đáy là tam giác đều cạnh 2a . Cạnh bên SA vuông góc với mặt phẳng ( ABC ) . Góc giữa cạnh bên SC và mặt đáy bằng 30 . Gọi I là trung điểm của BC . Tính khoảng cách từ điểm A đến đường thẳng: a) SB ; b) SC ; c) SI . Câu 27. Cho hình lập phương ABCD  A BC  D có cạnh bằng a . Tính khoảng cách từ đỉnh D đến đường chéo AC  . Câu 28. Cho hình chóp S . ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt phẳng đáy ( ABCD) và SA  a . Tính khoảng cách giữa hai đường thẳng: a) SB và AD ; b) BD và SC . Câu 29. Cho hình chóp S . ABC có đáy ABC là tam giác đều cạnh a , cạnh bên SA vuông góc với a 6 đáy. Tính khoảng cách từ điểm A đến mặt phẳng (SBC) theo a , biết SA  . 2 Câu 30. Cho hình chóp tam giác đều S . ABC có cạnh đáy bằng 3a , cạnh bên bằng 2a . Gọi G là trọng tâm của tam giác ABC, M là trung điểm của SC . a) Tính khoảng cách từ S đến mặt phẳng ( ABC ) . b) Tính khoảng cách từ M đến mặt phẳng ( SAG ) . Câu 31. Cho hình lập phương ABCD  A BC  D cạnh a . Gọi M , N lần lượt là trung điểm của AC và BC  . Tính khoảng cách giữa hai đường thẳng MN và B D . Câu 32. Cho tứ diện đều ABCD có cạnh bằng 11 . Gọi I là trung điểm của cạnh CD . Tính khoảng cách giữa hai đường thẳng AC và BI . 3a Câu 33. Cho hình chóp S . ABCD có đáy ABCD là hình thang vuông tại A và B với AB  2a ; BC  ; 2 AD  3a . Hình chiếu vuông góc của S lên mặt phẳng  ABCD  là trung điểm H của BD . Biết góc giữa mặt phẳng  SCD  và mặt phẳng  ABCD  bằng 600 . Tính khoảng cách a) từ C đến mặt phẳng  SBD  . b) từ B đến mặt phẳng  SAH  . Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  9. Điện thoại: 0946798489 TOÁN 11-CÁNH DIỀU Câu 34. Cho hình chóp S . ABCD có đáy ABCD là hình thang vuông tại A và B với AB  BC  2 a ; AD  3a . Hình chiếu vuông góc của S lên mặt phẳng  ABCD  là trung điểm H của AC . Biết góc giữa  SBC  và  ABCD  bằng 60 . Tính khoảng cách: a) Từ H đến  SAB  . b) Từ H đến  SCD  . c) Từ H đến  SBD  . Câu 35. Cho hình chóp S . ABCD có đáy ABCD là hình chữ nhật, biết AB  2a , AD  a 3 . Tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. a) Tính khoảng cách từ A đến mặt phẳng  SBC  . b) Tính khoảng cách từ A đến mặt phẳng  SCD  . c) Tính khoảng cách từ A đến mặt phẳng  SBD  . d) Gọi M là trung điểm của AB . Tính khoảng cách từ A đến mặt phẳng  SCM  và khoảng cách từ A đến mặt phẳng  SDM  . Câu 36. Cho tứ diện S . ABC có tam giác ABC vuông cân đỉnh B , AB  a , SA vuông góc với mặt phẳng  ABC  và SA  a . a) Chứng minh  SAB    SBC  . b) Tính khoảng cách từ điểm A đến  SBC  . c) Gọi I là trung điểm của AB . Tính khoảng cách từ điểm I đến  SBC  . d) Gọi J là trung điểm của AC . Tính khoảng cách từ điểm J đến  SBC  . e) Gọi G là trọng tâm tam giác ABC . Tính khoảng cách từ điểm G đến  SBC  . Câu 37. Cho hình chóp tứ giác S . ABCD , đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt phẳng  ABCD và SA  a 3 . O là tâm hình vuông ABCD . a) Tính khoảng cách từ điểm A đến  SBC  . b) Tính khoảng cách từ điểm O đến  SBC  . c) G1 là trọng tâm SAC . Từ G1 kẻ đường thẳng song song với SB cắt OB tại I . Tính khoảng cách từ điểm G1 đến  SBC  , khoảng cách từ điểm I đến  SBC  . d) J là trung điểm của SD . Tính khoảng cách từ điểm J đến  SBC  . e) Gọi G2 là trọng tâm của SDC . Tính khoảng cách từ điểm G2 đến  SBC  . Câu 38. Cho hình chóp S . ABCD có ABCD là hình vuông cạnh a , mặt bên SAB là tam giác đều cạnh a và  SAB  vuông góc với  ABCD  . Gọi I là trung điểm của cạnh AB , E là trung điểm của cạnh BC . a) Chứng minh  SIC    SED  . b) Tính khoảng cách từ điểm I đến  SED  . c) Tính khoảng cách từ điểm C đến  SED  . d) Tính khoảng cách từ điểm A đến  SED  . Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
  10. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ Câu 39. Cho hình chóp S. ABCD , CÓ SA   ABCD  và SA  a 6 , đáy ABCD là nửa lục giác đều nội tiếp trong đường tròn đường kính AD  2a . a) Tính các khoảng cách từ A và B đến mặt phẳng  SCD  . b) Tính khoảng cách từ đường thẳng AD đến mặt phẳng  SBC  . c) Tính diện tích của thiết diện của hình chóp S. ABCD với mặt phẳng  P  song song với  SAD  a 3 và cách  SAD  một khoảng bằng . 4 Câu 40. Cho hình chóp S. ABC có SA vuông góc với đáy; SA  a 3 . Tam giác ABC đều cạnh a. Tính khoảng cách a) SA và BC b) SB và CI với I là trung điểm của AB c) Từ B tới mặt phẳng  SAC  d) Từ J tới mặt phẳng  SAB  với J là trung điểm của SC Câu 41. Cho hình chóp S . ABCD có đáy là hình thang vuông tại A và B với AB  BC  2a, AD  3a. Hình chiếu vuông góc của S lên mặt phẳng  ABCD  là điểm H thuộc AB với AH  HB . Biết góc giữa mặt phẳng  SCD  và mặt phẳng  ABCD  bằng 600 . a)Tính góc giữa CD và SB b)Tính khoảng cách từ A đến mặt phẳng  SCD  c)Tính khoảng cách từ O đến mặt phẳng  SBC  d)Tính khoảng cách giữa hai đường thẳng AD và SB e)Tính khoảng cách giữa hai đường thẳng AC và SE với E là điểm thuộc AD sao cho AE  a Câu 42. Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật với AD  AB  2a . Gọi M là trung   điểm CD . Tam giác SAM cân và nằm trong mặt phẳng vuông góc với đáy.Biết SD;  ABCD    với 1 6a cos   và khoảng cách từ A đến mặt phẳng  SCD  bằng . 3 5 a)Tính khoảng cách từ C đến  SAD  . 1 b)Tính khoảng cách gữa hai đường thẳng SA và DN , với N  BC và CN  BN . 3 Câu 43. Cho hình chóp tứ giác S . ABCD , đáy ABCD là hình chữ nhật với AB  a; AD  a 3 , tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm AB . Tính khoảng cách: a) từ A tới mặt phẳng  SBD  .B) giữa hai đường SH và CD . c) giữa hai đường SH và AC .d) giữa hai đường SB và CD . e) giữa hai đường BC và SA .f) giữa hai đường SC và BD . Câu 44. Cho hình chóp tam giác S. ABC , đáy ABC là tam giác đều cạnh 2a . Gọi I là trung điểm của 1 BC , hình chiếu vuông góc của S lên mặt phẳng  ABC  là điểm H thuộc đoạn AI sao cho AH  HI . 2 Biết góc giữa SC và mặt đáy bằng 60 . Tính khoảng cách a) từ M đến mặt phẳng  SAI  , với M là trung điểm của SC . b) giữa hai đường thẳng SA và BC . c) giữa hai đường SB với AM , với M là trung điểm của SC . Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  11. Điện thoại: 0946798489 TOÁN 11-CÁNH DIỀU Câu 45. Cho hình chóp S . ABCD có đáy ABCD là hình chữ nhật với AB  a 2; AD  2a . Biết tam giác a2 6 SAB là tam giác cân tại S , nằm trong mặt phẳng vuông góc với đáy và có diện tích bằng . Gọi H là 6 trung điểm của AB . Tính khoảng cách a) từ A đến  SBD  . b) giữa hai đường thẳng SH và BD . c) giữa hai đường thẳng BC và SA . Dạng 2. Ứng dụng Câu 46. (SGK - Cánh diều 11 - Tập 2) Người ta dựng các cột đèn vuông góc với mặt đường, trong đó mỗi cột đèn gợi nên hình ảnh một đường thẳng. Khoảng cách giữa hai chân cột đèn liên tiếp đo được là 5 m . Tại sao có thể nói khoảng cách giữa hai cột đèn đó là 5 m ? Câu 47. (SGK - Cánh diều 11 - Tập 2) Hình 76 gợi nên hình ảnh hai mặt phẳng ( P) và (Q) song song với nhau. Cột gỗ cao 4,2 m. Khoảng cách giữa ( P) và (Q) là bao nhiêu mét? Câu 48. Một chiếc máy bay cất cánh từ một điểm thuộc mặt đất phẳng nằm ngang. Trong 3 phút đầu máy bay bay với vận tốc 500 km / h và theo đường thẳng tạo với mặt đất một góc 15 . Hỏi sau 2 phút, máy bay ở độ cao bao nhiêu kilômét (làm tròn kết quả đến chữ số thập phân thứ nhất)? Câu 49. Trên một mái nhà nghiêng 30 so với mặt phẳng nằm ngang, người ta dựng một chiếc cột vuông góc với mái nhà. Hỏi chiếc cột tạo với mặt phẳng nằm ngang một góc bao nhiêu độ? Vì sao? Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
  12. TOÁN 11-CÁNH DIỀU Điện thoại: 0946798489 BÀI 5. KHOẢNG CÁCH • CHƯƠNG 8. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN • |FanPage: Nguyễn Bảo Vương PHẦN C. BÀI TẬP TRẮC NGHIỆM (PHÂN MỨC ĐỘ) 1. Câu hỏi dành cho đối tượng học sinh trung bình – khá Câu 1. Cho hình chóp tứ giác đều S . ABCD có cạnh đáy là a 2 và tam giác SAC đều. Tính độ dài cạnh bên của hình chóp. A. 2a . B. a 2 . C. a 3 . D. a . Câu 2. Cho tứ diện ABCD có AC  3a, BD  4a . Gọi M , N lần lượt là trung điểm AD và BC . Biết AC vuông góc BD . Tính MN . 5a 7a a 7 a 5 A. MN  . B. MN  . C. MN  . D. MN  . 2 2 2 2 Câu 3. Cho hình chóp S . ABC có đáy là tam giác đều cạnh a , SA   ABC  , góc giữa hai mặt phẳng  ABC  và  SBC  là 60  . Độ dài cạnh SA bằng 3a a a A. . B. . C. a 3 . D. . 2 2 3 Câu 4. Cho hình lăng trụ ABC.ABC  có tất cả các cạnh đều bằng a . Góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30 . Hình chiếu H của A trên mặt phẳng  AB C   là trung điểm của BC  . Tính theo a khoảng cách giữa hai mặt phẳng đáy của lăng trụ ABC.ABC  . a a a 3 a 2 A. . B. . C. . D. . 2 3 2 2 Câu 5. Cho hình hộp chữ nhật ABCD. A ' B ' C ' D ' có AD  2 a , CD  a , AA '  a 2 . Đường chéo AC ' có độ dài bằng A. a 5 . B. a 7 . C. a 6 . D. a 3 . Câu 6. Cho hình chóp S. ABC có SA   ABC  , SA  AB  2a , tam giác ABC vuông tại B (tham khảo hình vẽ). Khoảng cách từ A đến mặt phẳng  SBC  bằng A. a 3 . B. a . C. 2a . D. a 2 . Câu 7. Cho hình chóp SABC có đáy là tam giác vuông tại A , AB  a , AC  a 3 , SA vuông góc với mặt phẳng đáy và SA  2a . Khoảng cách từ điểm A đến mặt phẳng  SBC  bằng Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
  13. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ a 57 2a 57 2a 3 2a 38 A. . B. . C. . D. . 19 19 19 19 Câu 8. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , 2SA  AC  2a và SA vuông góc với đáy. Khoảng cách từ A đến mặt phẳng  SBC  là 2a 6 4a 3 a 6 a 3 A. . B. . C. . D. . 3 3 3 3 Câu 9. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SB vuông góc với mặt phẳng đáy. Biết SB  3a , AB  4 a, BC  2 a . Khoảng cách từ B đến mặt phẳng ( SAC ) bằng 12 61a 3 14a 4a 12 29a A. . B. . C. . D. . 61 14 5 29 Câu 10. Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B , AB  a , SA vuông góc với mặt phẳng đáy và SA  2a . Khoảng cách từ A đến mặt phẳng  SBC  bằng 2 5a 5a 2 2a 5a A. . B. . C. . D. . 5 3 3 5 Câu 11. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a, SA vuông góc với mặt phẳng đáy và SA  a . Khoảng cách từ A đến mặt phẳng  SBC  bằng 5a 3a 6a 3a A. . B. . C. . D. . 3 2 6 3 Câu 12. Cho hình chóp S . ABC có đáy là tam giác vuông cân tại C, BC  a , SA vuông góc với mặt phẳng đáy và SA  a . Khoảng cách từ A đến mặt phẳng  SBC  bằng 2a a 3a A. 2a . B. . C. . D. . 2 2 2 Câu 13. Cho hình chóp S . ABC có đáy là tam giác vuông đỉnh B , AB  a , SA vuông góc với mặt phẳng đáy và SA  a . Khoảng cách từ điểm A đến mặt phẳng  SBC  bằng a a 6 a 2 A. . B. a . C. . D. . 2 3 2 Câu 14. Cho hình lập phương ABCD. AB C D  có cạnh bằng 1 . Tính khoảng cách d từ điểm A đến mặt phẳng  BDA  . 3 6 2 A. d  . B. d  . C. d  . D. d  3 . 3 4 2 Câu 15. Cho hình lăng trụ đứng ABCA' B'C ' có đáy là tam giác ABC vuông tại A có BC  2a , AB  a 3 , (tham khảo hình vẽ bên). Khoảng cách từ A đến mặt phẳng ( BCC ' B ' ) là Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  14. Điện thoại: 0946798489 TOÁN 11-CÁNH DIỀU a 5 a 7 a 3 a 21 A. . B. . C. . D. . 2 3 2 7 Câu 16. Cho hình chóp S.ABCD có đáy là hình vuông tâm O , SA vuông góc với mặt đáy. Hỏi mệnh đề nào sau đây là sai? A. d  B, SCD    2d  O, SCD   . B. d  A, SBD    d  B, SAC   . C. d  C, SAB    d  C, SAD   . D. d  S, ABCD    SA. Câu 17. Cho hình chóp S. ABCD có đáy ABCD là hình vuông tâm O , SA   ABCD  . Gọi I là trung điểm của SC . Khoảng cách từ I đến mặt phẳng  ABCD  bằng độ dài đoạn thẳng nào? A. IB . B. IC . C. IA . D. IO . Câu 18. Cho hình chóp tứ giác đều S. ABCD có đáy là hình vuông cạnh a . Gọi M là trung điểm của SD . Khoảng cách từ M đến mặt phẳng  SAC  bằng a 2 a 2 a a A. . B. . C. . D. . 2 4 2 4 Câu 19. Cho tứ diện đều S. ABCD có tất cả các cạnh đều bằng 2a , gọi M là điểm thuộc cạnh $AD$ sao cho DM  2 MA . Tính khoảng cách từ M đến mặt phẳng  BCD  . 2a 6 4a 6 2a 6 A. . B. a 6 . C. . D. . 9 9 3 Câu 20. Cho tứ diện đều ABCD có cạnh bằng a . Khoảng cách từ A đến mặt phẳng  BCD  bằng: a 3 a 3 a 6 a 6 A. . B. . C. . D. . 4 3 3 2  Câu 21. Trong không gian cho tam giác ABC có ABC  90o , AB  a . Dựng AA’, CC’ ở cùng một phía và vuông góc với mặt phẳng  ABC  . Tính khoảng cách từ trung điểm của A’C’ đến  BCC ' . a a A. . B. a . C. . D. 2a . 2 3 Câu 22. Cho hình chóp S . ABCD có SA vuông góc với mặt đáy và đáy ABCD là hình chữ nhật. Biết AB  4 a , AD  3a , SB  5 a . Tính khoảng cách từ điểm C đến mặt phẳng  SBD  . 12 41 a 41 a 12 61 a 61 a A. . B. . C. . D. . 41 12 61 12 Câu 23. Cho hình lập phương ABCD.ABCD cạnh a . Tính khoảng cách giữa hai đường thẳng AB và CD . Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
  15. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ a 2 A. . B. a. C. a 2. D. 2a. 2 Câu 24. Cho tứ diện đều ABCD có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB và CD bằng a 2 a 2 a 3 a 3 A. . B. . C. . D. . 3 2 2 3 Câu 25. Cho hình chóp S .MNPQ có đáy là hình vuông, MN  3a , với 0  a   , biết SM vuông góc với đáy, SM  6a . Khoảng cách giữa hai đường thẳng NP và SQ bằng A. 6a . B. 3a . C. 2a 3 . D. 3a 2 . Câu 26. Cho hình hộp chữ nhật EFGH .E F G H  có EF  3a, EH  4a, EE   12a, với 0  a   . Khoảng cách giữa hai đường thẳng EF  và GH  bằng A. 12a . B. 3a . C. 2a . D. 4a . Câu 27. Cho hình chóp S . ABCD có đáy ABCD là hình vuông cạnh a . Đường thẳng SA vuông góc với mặt phẳng  ABCD  và SA  a . Tính khoảng cách d giữa hai đường thẳng SB và CD . A. d  2a . B. d  a 3 . C. d  a 2 . D. d  a . Câu 28. Cho hình lập phương ABCD. AB C D  có cạnh bằng a . Khoảng cách giữa hai đường thẳng BB và AC  bằng a 2 A. a 2 . B. a . C. a 3 . D. . 2 Câu 29. Cho hình chóp S . ABCD có đáy ABCD là hình vuông cạnh bằng a , SA   ABCD  , SA  a 3 . Gọi M là trung điểm SD . Tính khoảng cách giữa đường thẳng AB và CM . 2a 3 a 3 3a a 3 A. . B. . C. . D. . 3 2 4 4 Câu 30. Cho lập phương ABCD. ABC D có cạnh bằng a ( tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng BD và AC  bằng 3a A. 3a . B. a . C. . D. 2a . 2 Câu 31. Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB  a , BC  2a , SA vuông góc với mặt phẳng đáy và SA  a . Khoảng cách giữa hai đường thẳng BD , SC bằng a 30 4 21a 2 21a a 30 A. . B. . C. . D. . 6 21 21 12 Câu 32. Cho lăng trụ tam giác đều ABC. ABC  có AB  a , AA  2a . Khoảng cách giữa AB và CC  bằng Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  16. Điện thoại: 0946798489 TOÁN 11-CÁNH DIỀU 2a 5 a 3 A. . B. a . C. a 3 . D. . 5 2 Câu 33. Cho hình chóp tứ giác S . ABCD có đáy là hình chữ nhật cạnh AD  2a , SA   ABCD và SA  a . Khoảng cách giữa hai đường thẳng AB và SD bằng a 3 a 6 2a 5 A. . B. . C. . D. a 6 . 3 4 5 Câu 34. Cho tứ diện OABC có OA , OB , OC đôi một vuông góc với nhau và OA  a, OB  OC  2a. Gọi M là trung điểm của cạnh BC . Khoảng cách giữa hai đường thẳng OM và AC bằng: a 2 2a 5 a 6 A. . B. . C. a . D. . 2 5 3 Câu 35. Cho hình chóp S.ABCD có đáy ABCD là hình vuông với đường chéo AC  2a , SA vuông góc với mặt phẳng  ABCD  . Khoảng cách giữa hai đường thẳng SB và CD là a a A. . B. . C. a 2 . D. a 3 . 3 2 2. Câu hỏi dành cho đối tượng học sinh khá-giỏi Câu 36. Cho tứ diện ABCD có tam giác ABD đều cạnh bằng 2 , tam giác ABC vuông tại B , BC  3 . 11 Biết khoảng cách giữa hai đường thẳng chéo nhau AB và CD bằng . Khi đó độ dài cạnh CD là 2 A. 2. B. 2 . C. 1. D. 3. Câu 37. Cho hình bình hành ABCD . Qua A, B , C , D lần lượt vẽ bốn nửa đường thẳng Ax, By, Cz , Dt cùng phía so với  ABCD  song song với nhau và không nằm trong mặt phẳng  ABCD  . Một mặt phẳng    lần lượt cắt các nửa đường thẳng Ax, By, Cz , Dt tại A, B , C , D  thỏa mãn AA  2, BB  3, CC   4 . Hãy tính DD. A. 3. B. 7. C. 2. D. 5. Câu 38. Cho tứ diện ABCD có tam giác ABD đều cạnh bằng 2 , tam giác ABC vuông tại B , BC  3 . 11 Biết khoảng cách giữa hai đường thẳng chéo nhau AB và CD bằng . Khi đó độ dài cạnh CD là 2 A. 2. B. 2 . C. 1. D. 3. Câu 39. Cho hình chóp S . ABCD có SA   ABCD  , SA  2a , ABCD là hình vuông cạnh bằng a . Gọi O là tâm của ABCD , tính khoảng cách từ O đến SC . a 2 a 3 a 3 a 2 A. . B. . C. . D. . 4 3 4 3 Câu 40. Một hình lập phương được tạo thành khi xếp miếng bìa carton như hình vẽ bên. Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
  17. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ Tính khoảng cách từ điểm O đến đường thẳng AB sau khi xếp, biết rằng độ dài đoạn thẳng AB bằng 2a . a 5 a 5 a 5 A. . B. . C. . D. a 5 . 2 4 3 Câu 41. Cho hình chóp S.ABC có tam giác ABC là tam giác vuông tại A , AC  a 3 ,   30 . Góc ABC giữa SC và mặt phẳng ABC bằng 60 . Cạnh bên SA vuông góc với đáy. Khoảng cách từ A đến  SBC  bằng bao nhiêu? a 6 a 3 2a 3 3a A. . B. . C. . D. 35 35 35 5 Câu 42. Cho hình chóp S .MNPQ có đáy là hình vuông cạnh MN  3a 2 , SM vuông góc với mặt phẳng đáy, SM  3a , với 0  a   . Khoảng cách từ điểm M đến mặt phẳng  SNP  bằng A. a 3 . B. 2a 6 . C. 2a 3 . D. a 6 . Câu 43. Cho hình chóp S . ABCD có đường cao SA  2 a , đáy ABCD là hình thang vuông ở A và D , AB  2 a, AD  CD  a . Khoảng cách từ điểm A đến mặt phẳng  SBC  bằng 2a 2a 2a A. . B. . C. . D. a 2. 3 2 3 Câu 44. Cho hình chóp S . ABC có SA vuông góc với mặt phẳng  ABC  , đáy ABC là tam giác vuông cân tại B , AC  a 2 . Gọi G là trọng tâm tam giác SAB và K là hình chiếu của điểm A trên cạnh SC . Gọi  là góc giữa hai mặt phẳng  ABC  và  AGK  . Tính cos  , biết rằng khoảng cách từ điểm A đến mặt a phẳng  KBC  bằng . 2 1 2 3 3 A. cos   . B. cos   . C. cos   . D. cos   . 2 2 2 3 Câu 45. Cho hình lập phương ABCD. A ' B ' C ' D ' cạnh a . Tính khoảng cách từ A đến mặt phẳng ( A ' BD) theo a . a 3 a 3 A. . B. a 3 . C. 2a 3 . D. . 3 6 Câu 46. Cho hình lăng trụ tam giác đều ABC . A ' B ' C ' có tất cả các cạnh bằng a . Khoảng cách từ A đến mặt phẳng  A ' BC  bằng a 12 a 21 a 6 a 3 A. . B. . C. . D. . 7 7 4 4 Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  18. Điện thoại: 0946798489 TOÁN 11-CÁNH DIỀU Câu 47. Cho hình lăng trụ đứng ABC. ABC  có đáy ABC là tam giác vuông tại A , AA  AC  a và AB  a 3 . Khoảng cách từ điểm A đến mặt phẳng ( A ' BC ) bằng a 21 a 3 a 21 a 7 A. . B. . C. . D. . 7 7 3 3 Câu 48. Cho tứ diện OABC có OA, OB, OC đôi một vuông góc. Biết OA  a, OB  2a, OC  a 3 . Tính khoảng cách từ điểm O đến mặt phẳng  ABC  . a 3 2a 3 a 17 a A. . B. . C. . D. . 2 19 19 19 Câu 49. Cho hình chóp tứ giác S . ABCD có đáy ABCD là hình bình hành tâm O ; mặt phẳng  SAC  vuông góc với mặt phẳng  SBD  . Biết khoảng cách từ O đến các mặt phẳng  SAB  ,  SBC  ,  SCD  lần lượt là 1; 2; 5 . Tính khoảng cách d từ O đến mặt phẳng  SAD  . 19 A. d  . 20 20 B. d  . 19 C. d  2 . 2 D. d  . 2 Câu 50. Cho hình chóp S . ABCD có đáy là hình chữ nhật, cạnh AB  2 AD  2 a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy  ABCD  Tính khoảng cách từ điểm A đến mặt phẳng  SBD  . a 3 a 3 a A. . B. . C. . D. a . 4 2 2 Câu 51. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a và chiều cao bằng a 3 . Khoảng cách từ A đến mặt phẳng  SCD  bằng. a 3 A. . B. a . C. a 3 . D. 2a . 2 Câu 52. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 4a. Gọi H là điểm thuộc đường thẳng     AB sao cho 3HA  HB  0 . Hai mặt phẳng  SAB  và  SHC  đều vuông góc với mặt phẳng đáy. Tính khoảng cách từ B đến mặt phẳng  SHC  . 5a 12a 6a 5a A. . B. . C. . D. . 6 5 5 12 Câu 53. Cho hình chóp S . ABCD có tất cả các cạnh đều bằng a . Gọi F là trung điểm của cạnh SA . Tính khoảng cách từ S đến mặt phẳng  FCD  ? 1 1 2 2 A. a. B. a. C. a. D. a. 2 5 11 9  Câu 54. Cho hình chóp S . ABC có SA vuông góc với mặt phẳng đáy. Biết góc BAC  30 , SA  a và BA  BC  a . Gọi D là điểm đối xứng với B qua AC . Khoảng cách từ B đến mặt phẳng ( SCD ) bằng Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
  19. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ 21 2 21 21 2 A. a. B. a. C. a. D. a. 7 7 14 2 Câu 55. Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AD  2a , SA vuông góc với đáy và SA  a 3 . Gọi H là hình chiếu của A lên SB . Khoảng cách từ H đến mặt phẳng  SCD  bằng a 6 3a 6 a 6 3a 6 A. . B. . C. . D. . 3 8 2 16 3a Câu 56. Cho hình chóp S. ABCD đáy là hình thoi tâm O cạnh a ,   60  , SA   ABCD  , SA  ABC . 2 Khoảng cách từ O đến mặt phẳng  SBC  bằng 3a 5a 3a 5a A. . B. . C. . D. . 8 8 4 4 Câu 57. Cho hình lăng trụ ABC . AB C  có đáy ABC là tam giác vuông tại A , AB  a, AC  2a . Hình chiếu vuông góc của A trên mặt phẳng  ABC  là điểm I thuộc cạnh BC . Tính khoảng cách từ A tới mặt phẳng  ABC  . 2 3 2 5 1 A. a. B. a. C. a. D. a. 3 2 5 3 Câu 58. Cho hình chóp S.ABCD có đáy là hình chữ nhật cạnh AB  2 AD  2a . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy  ABCD  . Tính khoảng cách từ A đến mặt phẳng  SBD  . a a 3 a 3 A. . B. . C. . D. a . 2 2 4 Câu 59. Cho hình chóp S . ABCD có đáy là hình vuông cạnh a , mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ A đến mặt phẳng  SBD  bằng 21a 21a 2a 21a A. . B. . C. . D. . 14 7 2 28 Câu 60. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy ( minh họa như hình vẽ bên). Khoảng cách từ C đến mặt phẳng ( SBD ) bằng 21a 21a 2a 21a A. . B. . C. . D. . 28 14 2 7 Câu 61. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ bên). Khoảng cách từ D đến mặt phẳng  SAC  bằng Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  20. Điện thoại: 0946798489 TOÁN 11-CÁNH DIỀU S A D B C a 21 a 21 a 2 a 21 A. . B. . C. . D. . 14 28 2 7 Câu 62. Cho hình chóp S . ABCD có đáy là hình vuông cạnh a , mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng  SAC  bằng 2a 21a 21a 21a A. . B. . C. . D. . 2 28 7 14  Câu 63. Cho hình chóp S . ABCD có đáy là hình thoi cạnh a , BAD  60 , SA  a và SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng  SCD  bằng a 21 a 15 a 21 a 15 A. . B. . C. . D. . 7 7 3 3  o Câu 64. Cho hình chóp S . ABCD có đáy ABCD là hình thoi cạnh a . Góc BAC  60 , hình chiếu của đỉnh S lên mặt phẳng  ABCD  trùng với trọng tâm của tam giác ABC , góc tạo bởi hai mặt phẳng  SAC  và  ABCD  là 60o . Khoảng cách từ B đến mặt phẳng  SCD  bằng 3a 3a 9a a A. . B. . C. . D. . 2 7 7 2 7 2 7 Câu 65. Cho hình chóp S . ABC có đáy ABC là tam giác vuông tại B biết BC  a 3 , BA  a . Hình chiếu vuông góc H của S trên mặt phẳng đáy là trung điểm của cạnh AC và biết thể tích khối chóp S . ABC bằng a3 6 . Tính khoảng cách d từ C đến mặt phẳng  SAB  . 6 a 30 2a 66 a 30 a 66 A. d  . B. d  . C. d  . D. d  . 5 11 10 11 Câu 66. Cho hình chóp S . ABCD có SA vuông góc với mặt phẳng  ABCD  . Tứ giác ABCD là hình vuông cạnh a , SA  2a . Gọi H là hình chiếu vuông góc của A trên SB . Tính khoảng cách từ H đến mặt phẳng  SCD  . 4a 5 4a 5 2a 5 8a 5 A. . B. . C. . D. . 5 25 5 25 Câu 67. Cho hình chóp S . ABCD có đáy ABCD là hình thang cân, đáy lớn AB . Biết AD  DC  CB  a, AB  2a, cạnh SA vuông góc với đáy và mặt phẳng  SBD  tạo với đáy góc 450 . Gọi I là trung điểm cạnh AB . Tính khoảng cách từ I đến mặt phẳng  SBD  . Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright ©2025 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
31=>1