
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 1
CHƯƠNG I. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
BÀI 1. HÀM SỐ LƯỢNG GIÁC
A. LÝ THUYẾT
I – ĐỊNH NGHĨA
1) Hàm số sin
Quy tắc đặt tương ứng với mỗi số thực
x
với số thực sin
x
sin :
sin
x
x
yx
=
được gọi là hàm số sin, kí hiệu là sin .yx=
Tập xác định của hàm số sin là .
2) Hàm số côsin
Quy tắc đặt tương ứng với mỗi số thực
x
với số thực cos
x
cos :
cos
x
x
yx
=
được gọi là hàm số sin, kí hiệu là cos .yx=
Tập xác định của hàm số cô sin là .
3) Hàm số tang
Hàm số tang là hàm số được xác định bởi công thức
()
sin cos 0 ,
cos
x
yx
x
=¹ kí hiệu là
tan .yx=
Tập xác định của hàm số tanyx= là D\ , .
2kk
pp
ìü
ïï
ïï
=+Î
íý
ïï
ïï
îþ
4) Hàm số côtang
Hàm số côtang là hàm số được xác định bởi công thức
()
cos sin 0 ,
sin
x
yx
x
=¹
kí hiệu là
cot .yx=
Tập xác định của hàm số cotyx= là
{
}
D\, .kkp=Î
II – TÍNH TUẦN HOÀN VÀ CHU KÌ CỦA HÀM SỐ LƯỢNG GIÁC
1) Định nghĩa
Hàm số
()
yfx= có tập xác định D được gọi là hàm số tuần hoàn, nếu tồn tại một số
0T¹ sao cho với mọi DxÎ ta có:
● DxT-Î và D.xT+Î
●
()()
f
xT fx+= .

Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 2
Số dương T nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì của hàm số tuần
hoàn đó.
Người ta chứng minh được rằng hàm số sinyx= tuần hoàn với chu kì 2Tp=; hàm số
cosyx= tuần hoàn với chu kì 2Tp=; hàm số tanyx= tuần hoàn với chu kì Tp=; hàm
số cotyx= tuần hoàn với chu kì .Tp=
2) Chú ý
● Hàm số
()
sinyaxb=+ tuần hoàn với chu kì 0
2
Ta
p
=.
● Hàm số
()
cosyaxb=+
tuần hoàn với chu kì 0
2
Ta
p
=.
● Hàm số
()
tanyaxb=+ tuần hoàn với chu kì 0
Ta
p
=.
● Hàm số
()
cotyaxb=+
tuần hoàn với chu kì 0
Ta
p
=.
● Hàm số
()
1
yfx= tuần hoàn với chu kì 1
T và hàm số
()
2
yfx= tuần hoàn với chu kì 2
T
thì hàm số
() ()
12
yfx fx= tuần hoàn với chu kì 0
T là bội chung nhỏ nhất của 1
T và 2
T.
Lưu ý 2 số thực không xác đinh được bội chung nn, nên là 012
TmTnT
với m,n là 2 số
tự nhiên nguyên tố cùng nhau )
III – SỰ BIẾN THIÊN VÀ ĐỒ THỊ CỦA HÀM SỐ LƯỢNG GIÁC
1) Hàm số sinyx=
● Tập xác định D=, có nghĩa và xác định với mọi ;xÎ
● Tập giá trị
[
]
1;1T=- , có nghĩa 1sin 1;x-£ £
● Là hàm số tuần hoàn với chu kì 2,p có nghĩa
()
sin 2 sin
x
kxp+= với ;kÎ
● Hàm số đồng biến trên mỗi khoảng 2; 2
22
kk
pp
pp
æö
÷
ç-+ + ÷
ç÷
ç
èø
và nghịch biến trên mỗi khoảng
3
2; 2
22
kk
pp
pp
æö
÷
ç++
÷
ç÷
ç
èø
,;kÎ
● Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng.
2) Hàm số cosyx=
● Tập xác định D=, có nghĩa và xác định với mọi .xÎ
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 3
● Tập giá trị
[
]
1;1T=- , có nghĩa 1cos 1;x-£ £
● Là hàm số tuần hoàn với chu kì 2,p có nghĩa
()
cos 2 cos
x
kxp+= với ;kÎ
● Hàm số đồng biến trên mỗi khoảng
()
2;2kkppp-+ và nghịch biến trên mỗi khoảng
()
2; 2kkpp p+,;kÎ
● Là hàm số chẵn nên đồ thị nhận trục tung làm trục đối xứng.
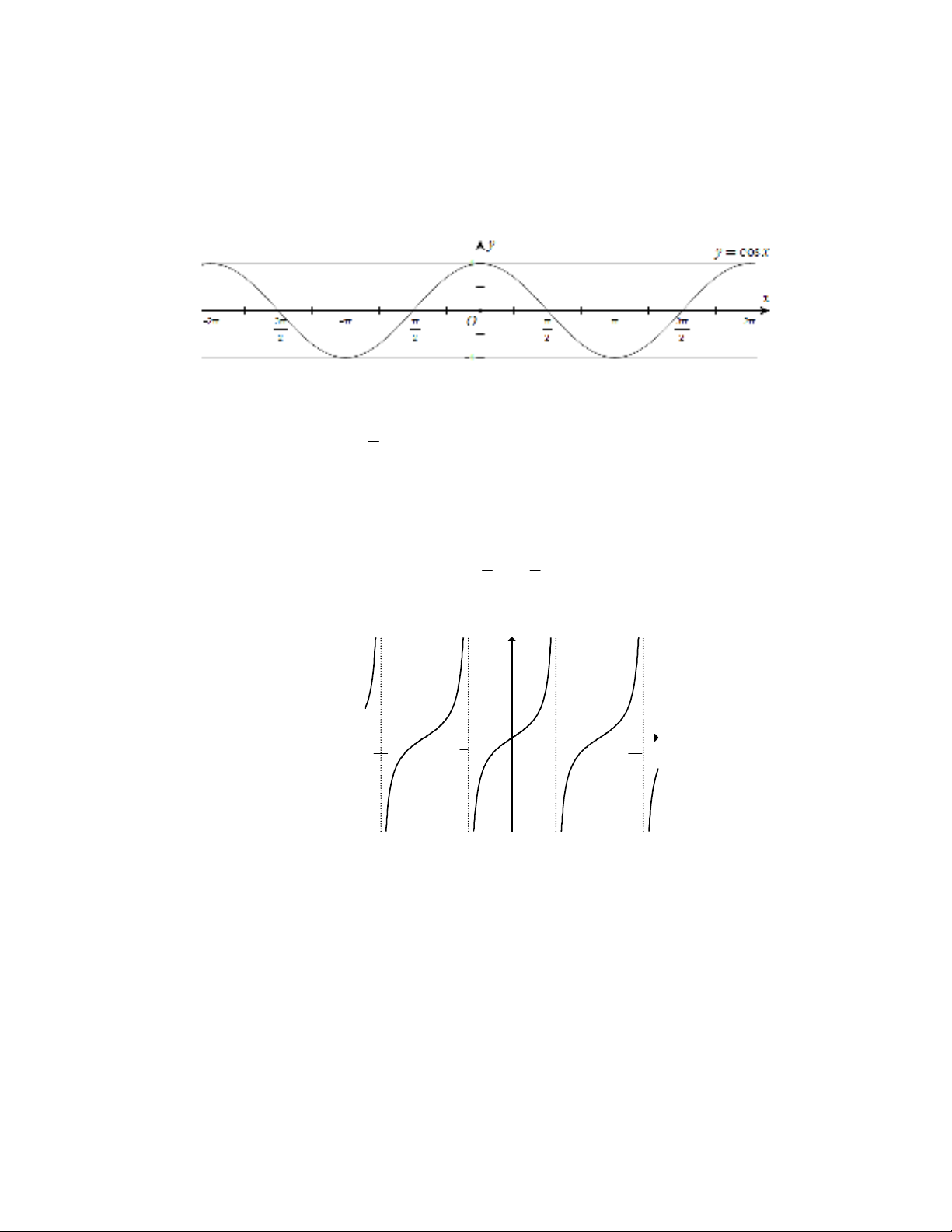
3) Hàm số tanyx=
● Tập xác định D\ , ;
2kk
pp
ìü
ïï
ïï
=+Î
íý
ïï
ïï
îþ
● Tập giá trị ;T=
● Là hàm số tuần hoàn với chu kì ,p có nghĩa
()
tan tan
x
kxp+= với ;kÎ
● Hàm số đồng biến trên mỗi khoảng ;, ;
22
kkk
pp
pp
æö
÷
ç-+ + Î
÷
ç÷
ç
èø
● Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng.
x
2
p
-
p-
y
2
p
O
3
2
p
-
p
3
2
p
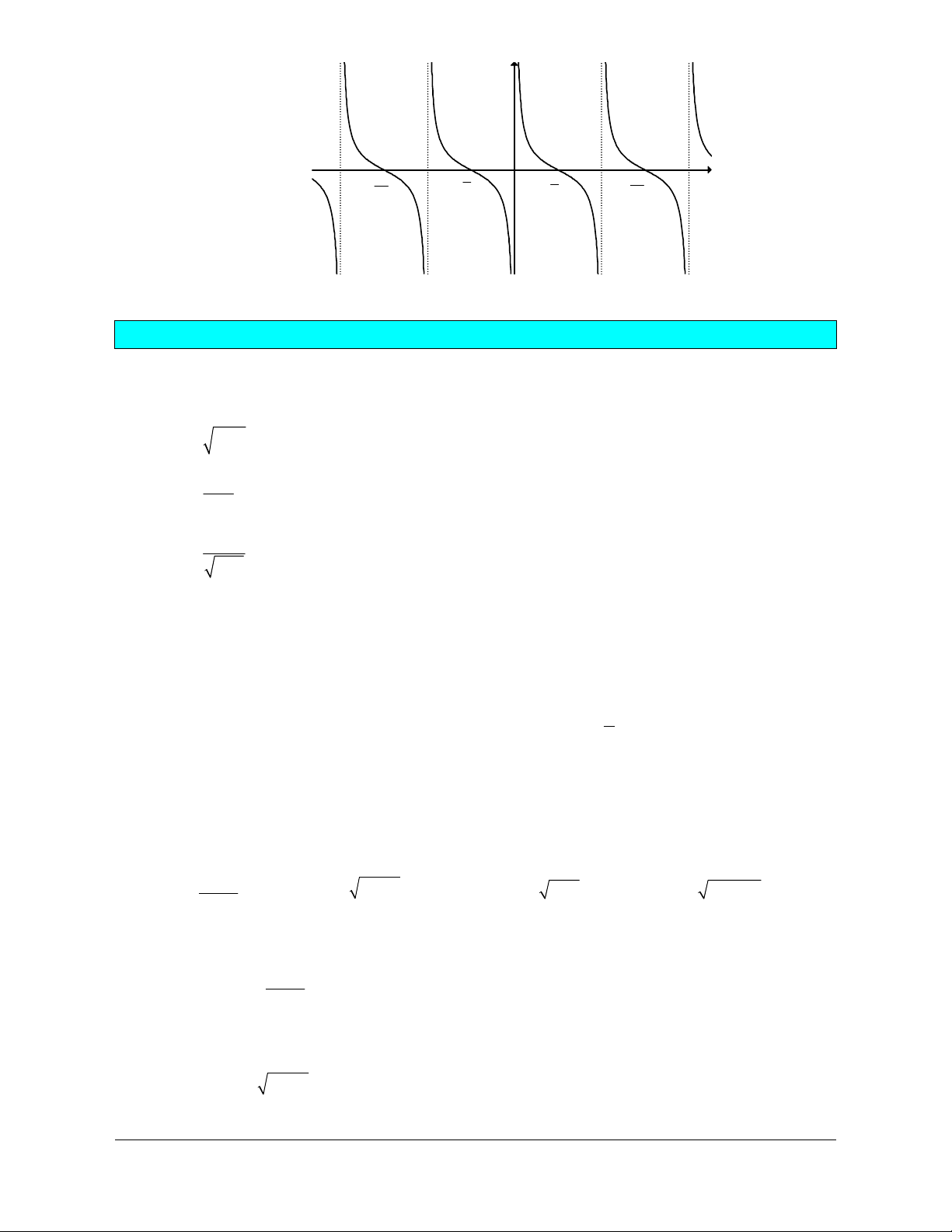
4) Hàm số cotyx=
● Tập xác định
{
}
D\, ;kkp=Î
● Tập giá trị ;T=
● Là hàm số tuần hoàn với chu kì ,p có nghĩa
()
tan tan
x
kxp+= với ;kÎ
● Hàm số đồng biến trên mỗi khoảng
()
;, ;kkkpp p+Î
● Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng.
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 4
x
2
p
-
p-
y
2
p
O
3
2
p
-
p
3
2
p
2p-
2p
B. PHÂN LOAIJVAF PHƯƠNG PHÁP GIẢI BAIF TÂP
Dạng 1: Tìm tập xác đinh của hàm số
1. Phương pháp
Để tìm tập xác định của hàm số ta cần lưu ý các điểm sau
yux có nghĩa khi và chỉ khi
ux xác định và u(x) 0.
u(x)
yv(x)
có nghĩa khi và chỉ
ux,
vx xác định và v(x) 0
.
u(x)
yv(x)
có nghĩa khi và chỉ
ux,
vx xác định và v(x) 0.
Hàm số y sinx, y cosx
xác định trên
và tập giá trị của nó là:
1sinx1; 1cosx1.
Như vậy,
ysinux,ycosux
xác định khi và chỉ khi
ux xác định.
ytanux có nghĩa khi và chỉ khi
ux xác định và
ux k,k
2
ycotux có nghĩa khi và chỉ khi
ux xác định và xk,k
.
2. Các ví dụ mẫu
Ví dụ 1. Tìm tập xác định của các hàm số sau:
a) 2
5x
ysin
x1
; b) 2
ycos4x;
c) ysinx; d)
y2sinx .
Giải
a) Hàm số 2
5x
ysin
x1
xác định 2
x10 x 1.
Vậy
D\1.
b) Hàm số 2
ycosx 4
xác định
22
4x 0 x 4 2x2.

Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 5
Vậy
Dx |2x2.
c) Hàm số ysinx xác định sinx 0 k2 x k2 ,k .
Vậy
Dx |k2x k2,k .
d) Ta có: 1 sinx 1 2 sinx 0 .
Do đó, hàm só luôn luôn xác định hay D.
Ví dụ 2. Tìm tập xác định của các hàm số sau:
a) ytanx6
; b)
ycotx ;
3
c) sinx
y;
cos(x )
d) 1
y.
tanx 1
Giải
a) Hàm số ytanx6
xác định 2
xkxk,k.
62 3
Vậy
2
D\ k,k .
3
b) Hàm số ycotx3
xác định xkx k,k.
33
Vậy D\ k,k .
3
c) Hàm số
sinx
ycos(x ) xác định
3
cos x 0 x k x k ,k .
22
Vậy 3
D\ k,k .
2
d) Hàm số 1
ytanx 1
xác định
tanx 1 x k ,k .
4
Vậy D\ k,k .
4
Ví dụ 3. Tìm tập xác định của các hàm số sau:
a)
1
ycos2x ;
cosx b) 3cos2x
y.
sin3xcos3x
Giải
a) Hàm số
1
ycos2xcosx xác định cosx 0 x k ,k .
2
Vậy
D\ k,k .
2



![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)










![Phiếu bài tập cuối tuần Tiếng Việt 1 tuần 2 đề 2: [Hướng dẫn chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250728/thanhha01/135x160/42951755577464.jpg)

