ÔN TẬP TOÁN 11 HKI
TRỊNH ĐĂNG DƯƠNG – LỚP 11A1 – TRƯỜNG THPT TRẦN QUỐC TUẤN
PHẦN ĐẠI SỐ
CÔNG THỨC LƯỢNG GIÁC.
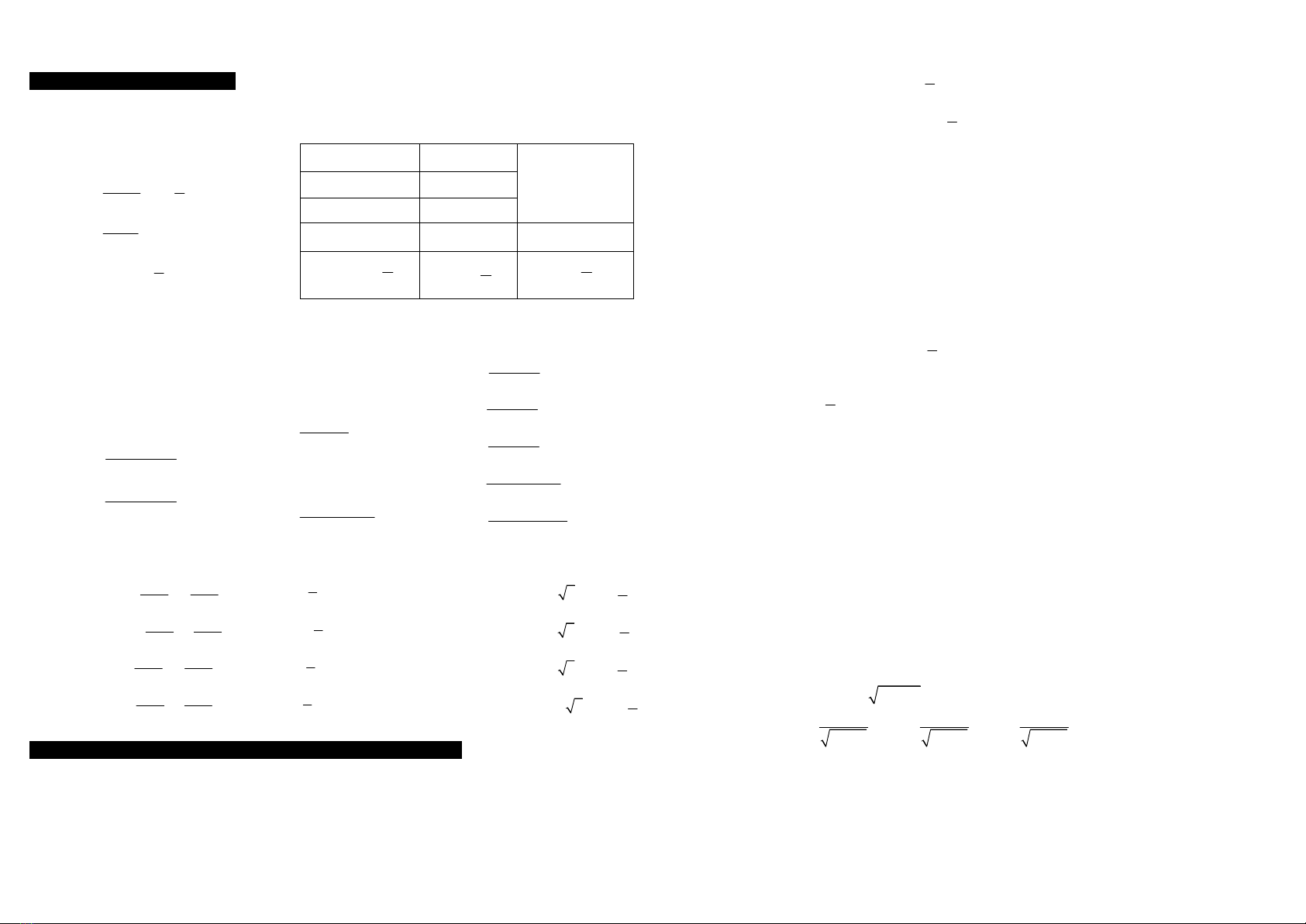
1. Công thức cơ bản 2. Cung liên quan đặc biệt
Cung Tính chất
Đ
ối: x & (-x) cosx=cos(-x)
Bù:
x & (π-x) sinx=sin(π-x)
Còn các hàm số
vòng khác thì
đối nhau
Khác
π: x & (π+x) tanx=tan(π+x) cot x = cot (π+x)
Ph
ụ: x & (
π
2
-x) sinx=cos(
π
2
-x)
tanx=cot(
π
2
-x)
3. Công thức cộng 4. CT nhân đôi, ba 5. CT hạ bậc
cos(
α β) = cosαcosβ sinαsinβ
cos(
α β) = cosαcosβ sinαsinβ
sin(
α β) = sinαcosβ cosαsinβ
sin(
α β) = sinαcosβ cosαsinβ
tanα tanβ
tan(α β) = 1 tanαtanβ
tanα tanβ
tan(α β) = 1 tanαtanβ
2
2
2
3
3
1 cos2α
cos α = 2
1 cos2α
sin α = 2
1 cos2α
tan α = 1 cos2α
3sin
α sin3α
sin α = 4
3cos
α cos3α
cos α =
4
6. CT biến tổng thành tích 7. CT biến tích thành tổng 8. CT khác
α β α β
cosα cosβ 2cos cos
2 2
α β α β
cosα cosβ 2sin sin
2 2
α β α β
sin α sin β 2sin cos
2 2
α β α β
sin α sin β 2 cos sin
2 2
1
cos
αcosβ [cos(α β) cos(α β)]
2
1
sin
αsinβ [cos(α β) cos(α β)]
2
1
sin
αcosβ [sin(α β) sin(α β)]
2
1
cos
αsinβ [sin(α β) sin(α β)]
2
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC.
1. Phương trình lượng giác cơ bản
a. Phương trình sin x = m
m [-1;1] : ptvn
m [-1;1] : m = sin
α
Vậy ta có phương trình: sin x = sin α
Chú ý:
π
sin x = 1 x = + k2π
2
π
sin x = 1 x = + k2
π
2
sin x = 0 x = kπ
(k
Z)
b. Phương trình cos x = m
m [-1;1] : ptvn
m [-1;1] : m = cos
α
Vậy ta có phương trình: cos x = cos α
Chú ý:
cos x = 1 x = k2π
cos x = 1 x =
π + k2π
π
cos x = 0 x = + k2
π
2
(k
Z)
c. Phương trình tan x = m
Điều kiện:
π
x k
π
2
Ta có phương trình: tan x = m = tan α
x =
α + kπ (k Z)
d. Phương trình cot x = m
Điều kiện:
x k
π
Ta có phương trình: cot x = m = cot α
x =
α + kπ (k Z)
2. Một số dạng phương trình lượng giác đơn giản
a. Dạng a.sin
2
x + b.sinx + c = 0
Đặt sinx = t (-1
t
1), phương trình trở thành: a.t
2
+ b.t + c = 0
Giải phương trình, tìm t
[-1;1]
Giải lại phương trình: sin x = t
b. Dạng a.sinx + b.cos x = c
Điều kiện: c
2
a
2
+ b
2
Chia 2 vế cho
2 2
a + b
, phương trình trở thành:
2 2 2 2 2 2
a b c
sin x + cos x =
a +b a +b a +b
cosα.sinx + sinα.cosx = m
sin(x+α) = m
c. Dạng a.sin
2
x + b.sinx.cosx + c.cos
2
x = d
Trường hợp 1. Xét cos x = 0 có phải là nghiệm của phương trình hay không.
Trường hợp 2. Xét cos x
0, chia hai vế cho cos
2
x, ta được phương trình:
a.tan
2
x + b.tanx + c = d(1 + tan
2
x)
Giải phương trình tìm tanx, sau đó tìm x.
2 2
2
2
2
2
sin α + cos α = 1
1 π
1 + tan
α = (α kπ,k Z)
cos α 2
1
1 + cot α = (α kπ,k Z)
sin α
π
tan α.cot α 1 (α k ,k Z)
2
2 2
2 2
2
3
3
3
2
sin2α = 2sinαcosα
cos2α = cos α sin α
= 2cos
α 1 1 2sin α
2tanα
tan2α = 1 tan α
sin3α = 3sinα 4sin α
cos3α = 4cos α 3cosα
3tanα tan α
tan3α = 1 3tan α
π
sin
α cos α 2sin(α )
4
π
2 cos(
α )
4
π
sin
α cos α 2 sin(α )
4
π
2 cos(
α )
4
x = α + k2π
(k Z)
x = π α + k2π
x = α + k2π
(k Z)
x = α + k2π
ÔN TẬP TOÁN 11 HKI
TRỊNH ĐĂNG DƯƠNG – LỚP 11A1 – TRƯỜNG THPT TRẦN QUỐC TUẤN
TỔ HỢP VÀ XÁC SUẤT
1. Hai quy tắc đếm cơ bản
a. Quy tắc cộng
Để thực hiện một công việc X có thể thực hiện phương án A hoặc phương án B
+ Phương án A có m cách thực hiện
+ Phương án B có n cách thực hiện
Vậy có (m+n) cách thực hiện công việc X.
b. Quy tắc nhân
Để thực hiện một công việc Y cần trải qua hai công đoạn A và B
+ Có m cách thực hiện công đoạn A
+ Có n cách tiếp tục thực hiện công đoạn B
Vậy có (m×n) cách thực hiện công việc Y
2. Hoán vị, chỉnh hợp, tổ hợp
a. Hoán vị: là một cách sắp xếp n phần tử của tập A theo một thứ tự
CT: P
n
= n! = 1.2.3. … . n
b. Chỉnh hợp: là một cách xếp k trong n phần tử của tập A, mỗi hoán vị của chỉnh hợp
cho một kết quả khác nhau.
CT: A
kn
= n.(n-1).(n-2). … .(n-k+1) =
n!
(n-k)!
c. Tổ hợp: là một tập con gồm k trong n phần tử của tập A, mỗi hoán vị của tổ hợp đều
cho một kết quả giống nhau.
CT: C
kn
=
k
n
A
n!
=
k! k!(n-k)!
Tính chất: C
kn
= C
n-kn
(Chú ý: C
on
= 1 = C
nn
; C
1n
= n = C
n-1n
)
C
kn
+ C
k-1n
= C
kn+1
3. Nhị thức Niu-tơn
CT:
4. Xác suất
Xác suất của biến cố A là:
A
Ω
P(A)=
Ω
Trong đó: Ω là không gian mẫu (tập tất cả các kết quả có thể xảy ra của một phép thử)
-Ω
A
là tập các kết quả thuận lợi cho A
Lưu ý: 0
P(A)
1
5. Các quy tắc tính xác suất
a. Quy tắc cộng:
P(A B) = P(A) + P(B)
khi A và B xung khắc nhau
P(A) + P(A) = 1 P(A) 1 P(A)
b. Quy tắc nhân: P(AB) = P(A).P(B) khi A và B độc lập nhau
PHẦN HÌNH HỌC
PHÉP BIẾN HÌNH
1. Phép tịnh tiến
Cho
(a;b), M(x,y). Gọi M’(x’;y’) là ảnh của M qua
u
T
. Ta có:
x' = x + a
y' = y + b
2. Phép đối xứng trục
a) Trục Ox: Gọi M’(x’;y’) là ảnh của M(x;y) qua Đ
Ox
. Ta có:
x' = x
y' = - y
b) Trục Oy: Gọi M’(x’;y’) là ảnh của M(x;y) qua Đ
Oy
. Ta có:
x' = - x
y' = y
3. Phép quay
Cho điểm O và góc lượng giác φ không đổi. Ta có: Q
(O;φ)
(M) = M’
OM = OM'
(OM;OM') =
φ
Trong mp Oxy, gọi M’(x’;y’) là ảnh của M(x;y) qua Q
(O;α)
thì:
x' = x.cos
α y.sinα
y' = x.sin
α y.cosα
4. Phép đối xứng tâm
Cho điểm O và M. Ta có: Đ
O
(M) = M’
O là trung điểm MM’
Cho M(x;y), I(a;b). Gọi M’(x’;y’) là ảnh của M qua Đ
I
. Ta có:
x' = 2a x
y' = 2a y
5. Phép vị tự
Phép vị tự tâm O tỉ số k
0 được kí hiệu là V
(O;k)
. V
(O;k)
(M) = M’
OM' = k. OM
HÌNH HỌC KHÔNG GIAN
1. Hai đường thẳng song song
a // c
b // c a // b
a,b phan biet
(P) (Q) = a a//b//c
(Q) (R) = b
a,b,c dong quy
(R) (P) = c
2. Đường thẳng song song mặt phẳng
a (P)
a // b a // (P)
b (P)
a // (P)
a (Q) b // a
(P) (Q) = b
(P) // a
(Q) // a a //
(P) (Q)
3. Hai mặt phẳng song song
a b = A trong (P)
a // (Q) (P) // (Q)
b // (Q)
n 0 n 1 n-1 1 2 n-2 2 k n-k k n-1 1 n-1 n n
n n n n n n
nk n-k k
n
k=0
(a+b) =C .a +C .a .b +C .a .b +...+C .a .b +...+C .a .
b +C .b
= C .a .b