PHÂN TÍCH H THANH BÊ TÔNG C T THÉPỆ Ố
CÓ XÉT Đ N Đ C TR NG BI N D NG C A BÊ TÔNGẾ Ặ Ư Ế Ạ Ủ
ANALYSIS OF REINFORCED CONCRETE FRAME STRUCTURE
CONSIDERING THE DEFORMATION CHARACTERISTIC OF CONCRETE
TR NH QUANG TH NHỊ Ị
Tr ng Đ i h c Bách khoa, Đ i h c Đà N ngườ ạ ọ ạ ọ ẵ
TÓM T TẮ
Phân tích h thanh bê tông c t thép có xét đ n đ c tr ng bi n d ng c a bê tông: bi n d ngệ ố ế ặ ư ế ạ ủ ế ạ
d o, khe n t... nh m đánh giá s phân b l i n i l c, đ k t qu phân tích chính xác h n vàẻ ứ ằ ự ố ạ ộ ự ể ế ả ơ
s d ng v t li u hi u qu h n.ử ụ ậ ệ ệ ả ơ
L p thu t toán xây d ng ma tr n đ c ng và vect ng l c nút c a ph n t thanh bê tôngậ ậ ự ậ ộ ứ ơ ứ ự ủ ầ ử
c t thép. K t h p v i ph ng pháp ph n t h u h n đ phân tích k t c u bê tông c t thépố ế ợ ớ ươ ầ ử ữ ạ ể ế ấ ố
trên máy tính đi n t .ệ ử
ABSTRACT
Analysis of reinforced – concrete frame structure with consideration to deformation
characteristic of concrete: plastic strain, cracks, and others is used to determine the
redistribution of stress, to achieve more accurate analysis results and to use materials more
effectively. The paper also presents the establishment of algorithm to build matrix of stiffness
and node stress vector of reinforced – concrete frame elements, and in combination with the
Finite Element Method to analyze reinforced-concrete structures on computer.
1. M đ uở ầ
Bi n d ng d o và s có m t c a các khe n t trong bê tông làm cho s phân b n iế ạ ẻ ự ặ ủ ứ ự ố ộ
l c trong các k t c u bê tông c t thép khá ph c t p.ự ế ấ ố ứ ạ
Các ph n m m đ phân tích k t c u công trình ph n nhi u là s d ng ph ng phápầ ề ể ế ấ ầ ề ử ụ ươ
ph n t h u h n. Tuy nhiên vi c xem xét m t cách đ y đ và chính xác nh h ng c aầ ử ữ ạ ệ ộ ầ ủ ả ưở ủ
bi n d ng ph c t p c a bê tông trong vi c xác đ nh đ c ng và ng l c nút c a các ph nế ạ ứ ạ ủ ệ ị ộ ứ ứ ự ủ ầ
t m u cho ph ng pháp ph n t h u h n còn h n ch .ử ẫ ươ ầ ử ữ ạ ạ ế
Bài vi t này mu n đ xu t m tế ố ề ấ ộ
bi n pháp k t h p các qui t c tính toánệ ế ợ ắ
hi n có đ gi i quy t khó khăn này. ệ ể ả ế
2. C s lý thuy tơ ở ế
Xét d m ch u u n v i t i tr ngầ ị ố ớ ả ọ
tăng d n: lúc đ u ch a b n t, toàn b ti tầ ầ ư ị ứ ộ ế
di n bê tông ch u ng su t, d m có đệ ị ứ ấ ầ ộ
c ng l n. T i tr ng tăng, bê tông có bi nứ ớ ả ọ ế
d ng d o, v t n t xu t hi n, t i ti t di nạ ẻ ế ứ ấ ệ ạ ế ệ
n t mô men quán tính gi m làm gi m rõứ ả ả
r t đ c ng c a d m.ệ ộ ứ ủ ầ
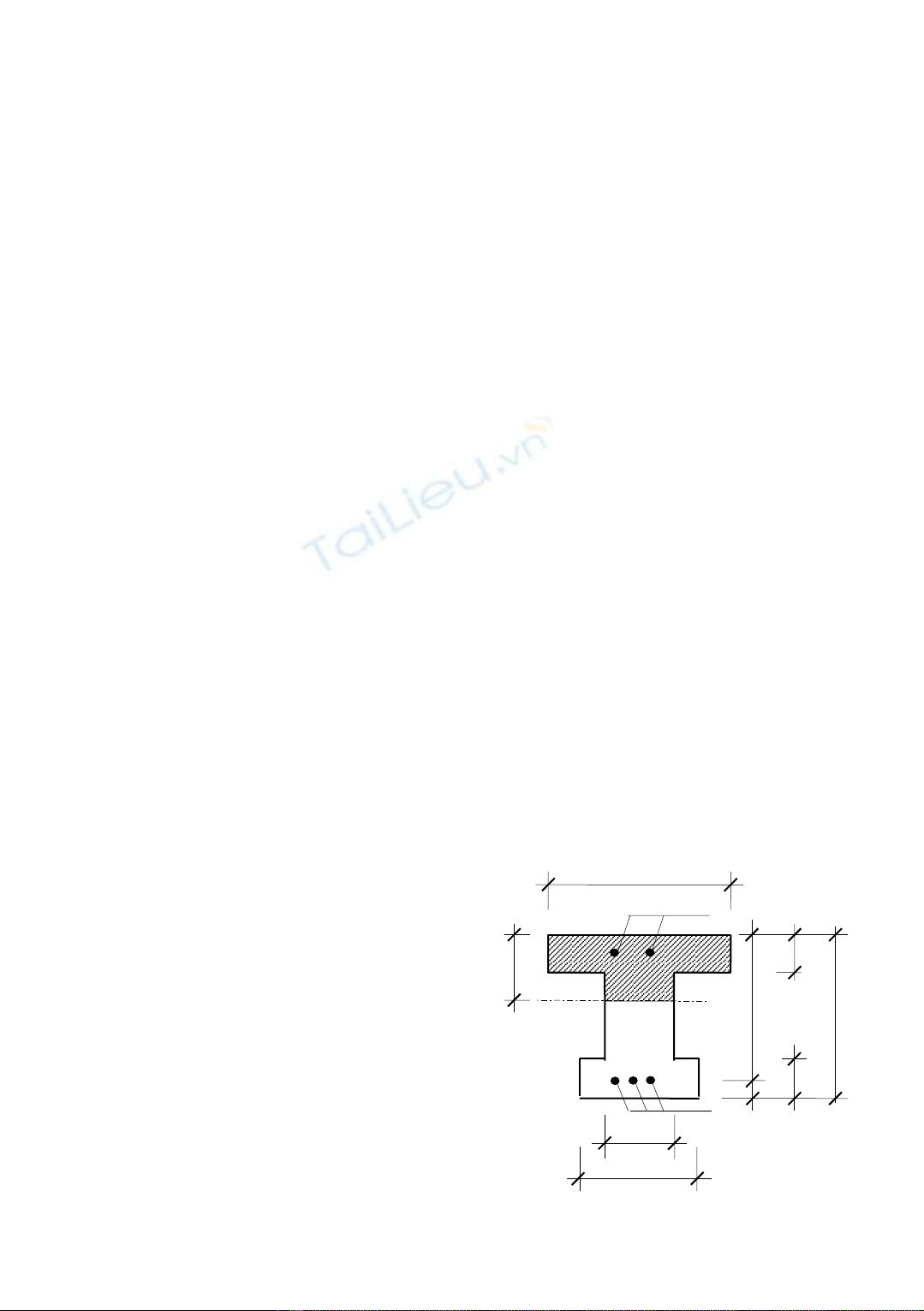
bc’
Fa’
hc’
hc
Fa
bc
h
b
x
a
h0
Hình 1: Ti t di n d m t i v trí khe n tế ệ ầ ạ ị ứ
2.1. Các đ c tr ng hình h c và bi n d ng c a c u ki n b ng bê tông c t thépặ ư ọ ế ạ ủ ấ ệ ằ ố
th ng sau khi xu t hi n khe n tườ ấ ệ ứ
* Di n tích mi n BT ch u nén qui đ i: ệ ề ị ổ
Fbqđ=(bc’ - b).hc’ +
n
ν
.Fa’ + b.x. (1 - 1)
* Đ c ng ch ng u n c a TD:ộ ứ ố ố ủ B =
+
bqdb
b
aa
a
FEFE
Zh
.
10
ν
ψψ
(1 - 2)
Trong đó:
ν là h s đàn h i c a bê tông.ệ ố ồ ủ
Ζ1 kho ng cách t h p l c vùng nén đ n tr ng tâm c t thép ch u kéo.ả ừ ợ ự ế ọ ố ị
ψb: H s xét đ n bi n d ng không đ u c a th bê tông ch u nén ngoài cùng, (l y =ệ ố ế ế ạ ề ủ ớ ị ấ
0.9 trong các tr ng h p bình th ng, khi ch u t i tr ng rung đ ng l y = 1).ườ ợ ườ ị ả ọ ộ ấ
ψa: H s xét s làm vi c ch u kéo c a bê tông; (ệ ố ự ệ ị ủ ψa ≤ 1)
* Đ c ng c a thanh khi ch u kéo (nén): EF ộ ứ ủ ị
C u ki n ch u kéo l ch tâmấ ệ ị ệ có l c d c Nự ọ c n m trong ph m vi gi a các tr ng tâmằ ạ ữ ọ
c t thép Fốa và Fa’:
;
).( '
a
aaa FFE
EF
ψ
+
=
(1 -
3)
C u ki n ch u nén l ch tâm:ấ ệ ị ệ
;
)...(
a
bqdbaa FEFE
EF
ψ
ν
+
=
(1 - 4)
2.2. Ma tr n đ c ng và vect ng l c nút t ng đ ng c a ph n t trongậ ộ ứ ơ ứ ự ươ ươ ủ ầ ử
ph ng pháp phàn t h u h nươ ử ữ ạ
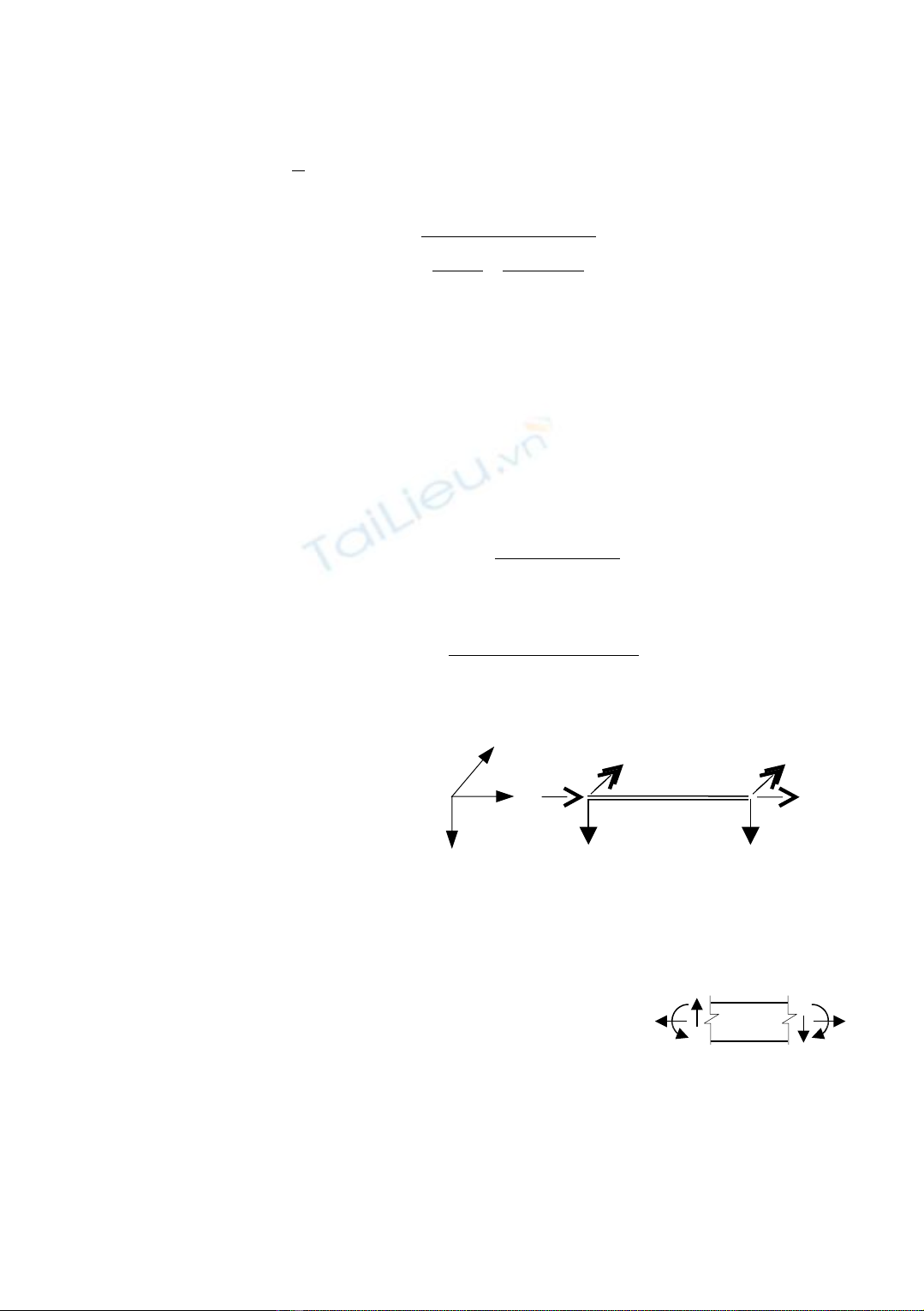
T ng quát v i ph n t thanhổ ớ ầ ử
lăng tr trong bài toán ph ng (h thanhụ ẳ ệ
ph ng):ẳ
G i qọ1, q2 là t i tr ng phân bả ọ ố
theo ph ng tr c 1, tr c 2, m là mô menươ ụ ụ
phân b . ố
G i tọ1, t2 là nhi t đ tăng lên m t d i và m t trên c a ph n t .ệ ộ ở ặ ướ ặ ủ ầ ử
Các thành ph n chuy n v {V} = {ầ ể ị u, v, ϕ} (u: chuy n vể ị
th ng d c tr c 1, v: chuy n v th ng theo tr c 2, ắ ọ ụ ể ị ắ ụ ϕ: chuy n vể ị
xoay quanh tr c 3ụ)
Và n i l cộ ự {F} = {N, Q, M.} (qui c d u theo hình vướ ấ ẽ
bên)
- Vect chuy n v nút {ơ ể ị δ} ≡ [δ1 δ2.. δ6]T ≡ [u1 v1 ϕ1 u2 v2 ϕ2]T;
- Vect ng l c nút {F} ơ ứ ự ≡ [F1 F2.. F6]T ≡ [N1 Q1 M1 N2 Q2 M2]T;
- Các quan h vi phân gi a chuy n v và n i l c:ệ ữ ể ị ộ ự
2
1
3
Hình 2: Ph n t thanh ph ngầ ử ẳ
u1 - N1
v1 - Q1
ϕ1 -
M1
v2 - Q2
ϕ2 -
M2
u2 - N2
NQ
M

dx
dM
dx
dQ
dx
dN
dx
d
dx
dv
dx
du
ϕ
=
−010000
000000
000000
.
1
00000
000100
00
.
1
000
JE
FE
x
M
Q
N
v
u
ϕ
+
−
−
−
−
+
m
q
ql
tt
tt
2
1
12
21
.2
.
0
2
.
α
α
; (2 - 1)
Hay
dx
dZ
= [A]. {Z} + {B}; (2 - 2)
Theo ph ng pháp ph n t h u h n - Mô hình chuy n v , có đ c ươ ầ ử ữ ạ ể ị ượ ph ng trình cươ ơ
b n c a ph n t h u h n: ả ủ ầ ử ữ ạ [K] {δ} = {F};
[K] -Ma tr n đ c ng c a ph n t .ậ ộ ứ ủ ầ ử
{δ} -Vect các chuy n v nút.ơ ể ị
{F} -Vect các l c nút t ng đ ng c a ph n tơ ự ươ ươ ủ ầ ử.
V i ph n t thanh có các đ c tr ng ti t di n không thay đ i, có th v i các phépớ ầ ử ặ ư ế ệ ổ ể ớ
khai tri n tích phân thông th ng, ho c v i các ti t di n quen thu c có th s d ng cácể ườ ặ ớ ế ệ ộ ể ử ụ
b ng tra l p s n đ xác đ nh các ph n t c a ma tr n đ c ng và vect ng l c nút t ngả ậ ẵ ể ị ầ ử ủ ậ ộ ứ ơ ứ ự ươ
đ ng c a ph n t .ươ ủ ầ ử
3. Ph ng pháp gi i v i c u ki n bê tông c t thépươ ả ớ ấ ệ ố
V i c u ki n bê tông c t thép, do các đ c tr ng c a ti t di n: đ c ng d c tr c EF,ớ ấ ệ ố ặ ư ủ ế ệ ộ ứ ọ ụ
đ c ng ch ng u n B (t ng đ ng v i EJ) xác đ nh theo (1-3), (1-12) là thay đ i nên ch aộ ứ ố ố ươ ươ ớ ị ổ ư
th gi i đ c nghi m đúng c a h ph ng trình trên. Trong tr ng h p này, có th gi iể ả ượ ệ ủ ệ ươ ườ ợ ể ả
theo ph ng pháp g n đúng Runge-Kutta (b c 4):ươ ầ ậ
Ph ng trình (2 - 2) đ c vi t l i: ươ ượ ế ạ
)(
..
..
)(
)(
2
1
xZ
xZ
xZ
dx
d
n
=
)(..)()(
........
........
)(..)()(
)(..)()(
21
22221
11211
xaxaxa
xaxaxa
xaxaxa
nnnn
n
n
x
)(
..
..
)(
)(
2
1
xZ
xZ
xZ
n
+
)(
..
..
)(
)(
2
1
xb
xb
xb
n
; (2 - 3)
Nghi m c a h ph ng trình t i x: ệ ủ ệ ươ ạ Z(x) = α(x).Z(0) + β(x); (2 - 4)
V i kho ng chia h, t i x+h có: ớ ả ạ Z(x+h) = α(x+h).Z(0) + β(x+h); (2 - 5)
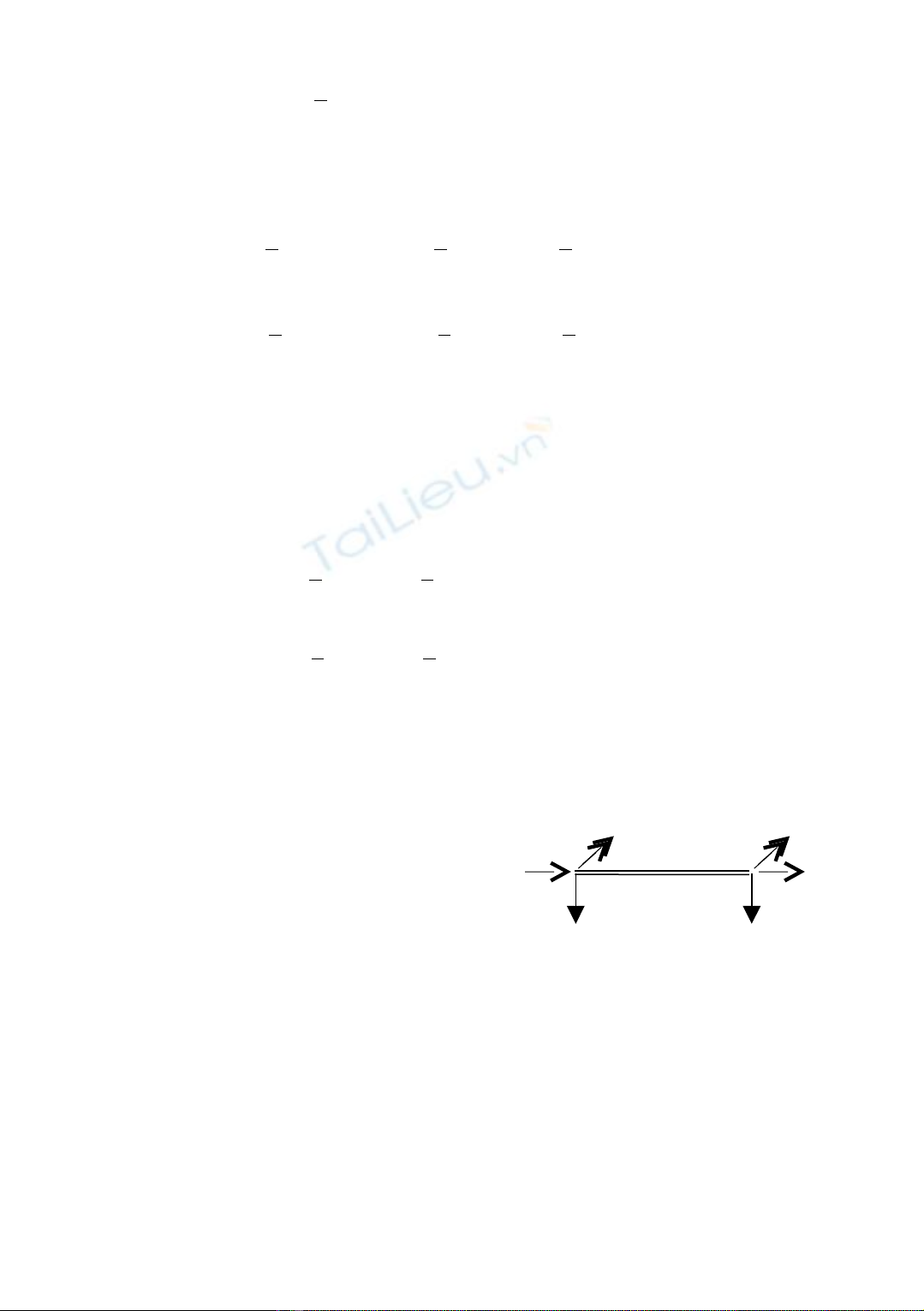
V i các công th c truy h i, có đ c s liên h c a các giá tr ớ ứ ồ ượ ự ệ ủ ị α và β 2 b c tíchở ướ
phân x và x+h nh sau:ư
( )
IV
iiiiiji KKKKxhx ++++=+ )(2
6
1
)()( ''''''
αβ
;
( )
IV
ijijijijijij KKKKxhx ++++=+ )(2
6
1
)()( ''''''
αα
;
V i:ớ
( )
+= ∑
=
n
pippii xaxxbhK
1
')().()(.
β
;
+
+++= ∑
=
n
pipppii h
xaKx
h
xbhK
1
''' )
2
(.
2
1
)()
2
(.
β
;
+
+++= ∑
=
n
pipppii h
xaKx
h
xbhK
1
''''' )
2
(.
2
1
)()
2
(.
β
;
( )( )
++++= ∑
=
n
pipppi
IV
ihxaKxhxbhK
1
''' )(.)()(.
β
;
Và:
( )
∑
=
=n
ppjipij xxahK
1
')().(.
α
;
∑
=
++= n
ppjpjipij Kx
h
xahK
1
'''
2
1
)().
2
(.
α
;
∑
=
++=
n
ppjpjipij
Kx
h
xahK
1
'''''
2
1
)().
2
(.
α
;
( )( )
∑
=++= n
ppjpjip
IV
ij KxhxahK
1
'''
)().(.
α
;
V y hàm Z(x) đ c xác đ nh v i m i đi m n u bi t Z(0) và v i các giá tr [ậ ượ ị ớ ọ ể ế ế ớ ị α(0)] =
[I] và {β(0)} = {0};
V i ph n t (ik), (2 – 4) s là: ớ ầ ử ẽ
Z(k) = α(k).Z(i) + β(k);
Hay
{ }
{ }
[ ] [ ]
[ ] [ ]
{ }
{ } { }
{ }
K
i
i
K
k
k
F
V
F
V
+
=
2
1
43
21 .
β
β
αα
αα
⇒ {Vk} = [α1]k.{Vi} + [α2]k.{Fi} + {β1}k; (2 - 6)
{Fk} = [α3]k.{Vi} + [α4]k.{Fi} + {β2}k; (2 - 7)
(2 - 6) ⇒ {Fi} =
[ ]
1
2−
k
α
.{Vk} -
[ ]
1
2−
k
α
.[α1]k.{Vi} -
[ ]
1
2−
k
α
.{β1}k;
(2 - 7) ⇒{Fk}=([α3]k-[α4]k.
[ ]
1
2−
k
α
.[α1]k).{Vi}+[α4]k.
[ ]
1
2−
k
α
.{Vk}-[α4]k.
[ ]
1
2−
k
α
.{β1}k)+{β2}k;
M t khác: {F} = [K] {ặδ} + {F0};
u1 - N1
v1 - Q1
ϕ1 - M1
v2 - Q2
ϕ2 - M2
u2 - N2
i
k
Hay:
{ }
{ }
[ ] [ ]
[ ]
[ ]
{ }
{ }
{ }
{ }
;.
0
0
,
,,
+
=
−
k
i
F
F
V
V
KkK
KK
F
F
k
i
iki
kikiik
k
i
V y, ma tr n đ c ng và vect ng l c nút t ng đ ng c a ph n t đang xét:ậ ậ ộ ứ ơ ứ ự ươ ươ ủ ầ ử
[ ]
iik
K,
=
[ ]
1
2−
k
α
.[α1]k;
[ ]
kik
K,
= -
[ ]
1
2−
k
α
;
{ }
0
i
F
=
[ ]
1
2−
k
α
.{β1}k;
[ ]
iki
K,
= [α3]k- [α4]k.
[ ]
1
2−
k
α
.[α1]k;
[ ]
kki
K,
= [α4]k.(
[ ]
1
2−
k
α
;
{ }
0
k
F
= {β2}k - [α4]k.
[ ]
1
2−
k
α
.{β1}k;
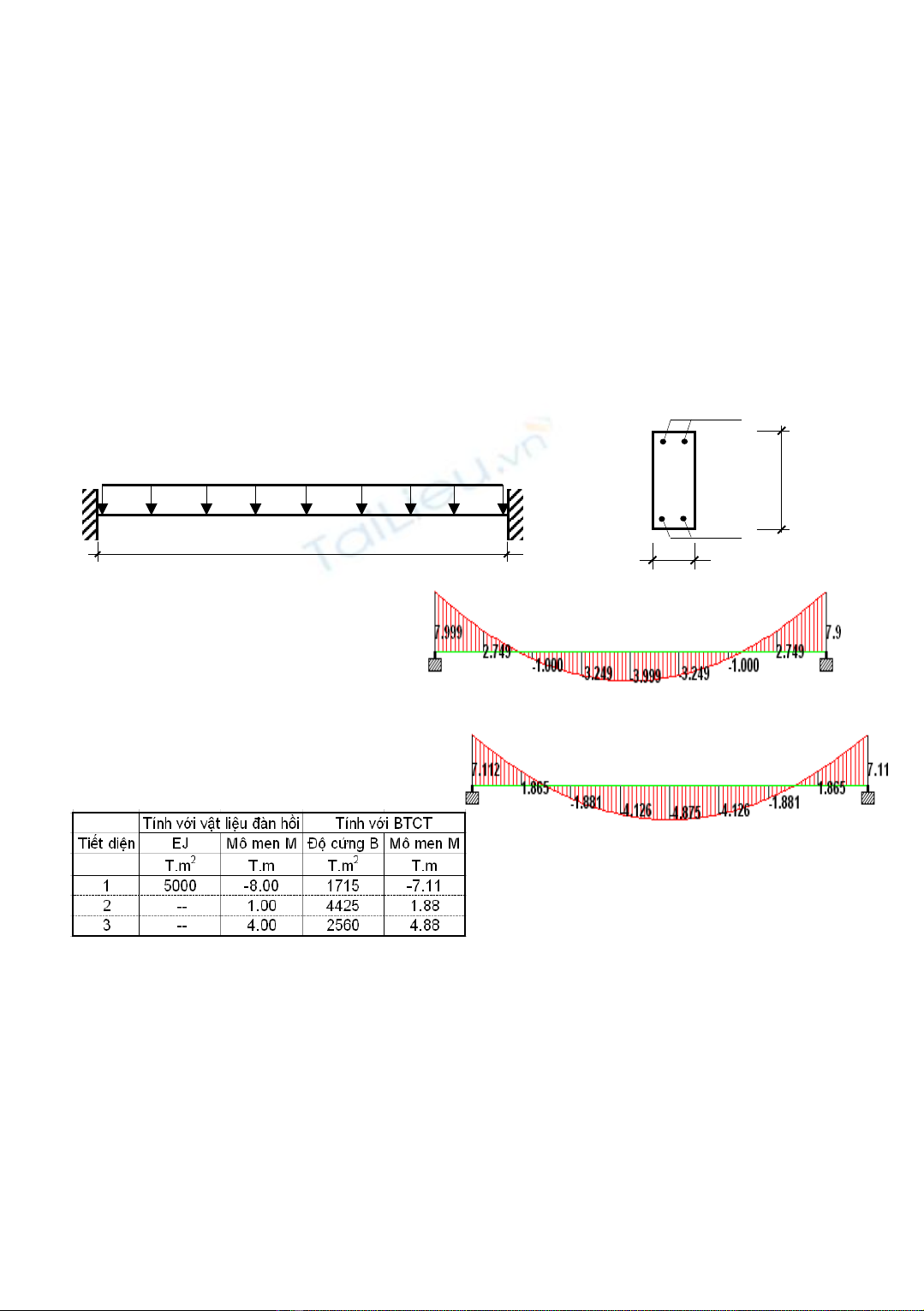
4. K t qu và th o lu nế ả ả ậ
Xét d m có s đ và ti t di n nh hình v ,ầ ơ ồ ế ệ ư ẽ
V i ti t di n ban đ u xem bêớ ế ệ ầ
tông là v t li u đàn h i, đ c ng c aậ ệ ồ ộ ứ ủ
d m là EJ= 5.10ầ3 T.m2; N i l c xácộ ự
đ nh đ c nh s đ .ị ượ ư ơ ồ
Xác đ nh đ c ng c a d m bê tôngị ộ ứ ủ ầ
c t thép theo (1-3), có đ c s phân b l iố ượ ự ố ạ
n i l c nh s đ sau:ộ ự ư ơ ồ
- Theo k t qu phân tích, n u có xét bi n d ng d o và n t trong bê tông thì đ c ngế ả ế ế ạ ẻ ứ ộ ứ
c a d m thay đ i đáng k . T i ti t di n có n i l c x p x gi i h n ch u l c, đ c ng cóủ ầ ổ ể ạ ế ệ ộ ự ấ ỉ ớ ạ ị ự ộ ứ
th gi m 2-3 l n đ c ng ban đ u.ể ả ầ ộ ứ ầ
- Giá tr c a h s đàn h i c a bê tông gi m nhi u khi ng su t tăng, do đó đ c ngị ủ ệ ố ồ ủ ả ề ứ ấ ộ ứ
c a d m không nh ng thay đ i nhi u h n, mà còn khác nhau nhi u gi a các ti t di n cóủ ầ ữ ổ ề ơ ề ữ ế ệ
n i l c chênh l ch l n. N u xét đ n y u t này s phân b l i n i l c càng rõ r t.ộ ự ệ ớ ế ế ế ố ự ố ạ ộ ự ệ
- Phân tích k t c u bê tông c t thép n u không xét s phân b l i n i l c do đế ấ ố ế ự ố ạ ộ ự ộ
c ng c a các c u ki n thay đ i s làm m t ý nghĩa c a nh ng c g ng chính xác hóa khiứ ủ ấ ệ ổ ẽ ấ ủ ữ ố ắ
tính toán ti t di n bê tông c t thép.ế ệ ố
2φ18
500
200 2φ20
q=1.5T/m
6m
1
3
2


























