
BỘ GIÁO DỤC VÀ ĐÀO TẠO
BỘ CÔNG THƯƠNG
VIỆN NGHIÊN CỨU ĐIỆN TỬ, TIN HỌC, TỰ ĐỘNG HÓA
===***===
PHÁT TRIỂN MỘT SỐ PHƯƠNG PHÁP HỌC TRỌNG SỐ
CHO MẠNG NƠ RON TẾ BÀO BẬC HAI
TÓM TẮT LUẬN ÁN TIẾN SĨ
Chuyên Ngành: Kỹ thuật điện tử
Mã số: 9520203
HÀ NỘI – NĂM 2024

1
MỞ ĐẦU
Thời đại số ở Việt Nam và trên thế giới đang sử dụng trí tuệ nhân tạo làm hạt nhân cho sự phát
triển, trong đó mạng nơ ron phỏng theo não người đang nổi lên như một công cụ hiện đại. Hai lớp
cấu trúc cơ bản của mạng nơ ron là mạng nơ ron truyền thẳng và mạng nơ ron hồi quy (phản hồi).
Mạng nơ ron hồi quy là một hướng phát triển có thể cấy trên các phần sụn (chương trình phần mềm
được ghi trên các chip phần cứng như bộ nhớ ROM) và đã được chế tạo thành máy tính nơ ron trên
thế giới. Chiếc máy tính này được phát triển dựa trên cấu trúc mạng nơ ron tế bào (do L. Chua và L.
Yang đề xuất năm 1988). Hướng phát triển của mạng nơ ron tế bào hiện nay bên cạnh về cấu trúc còn
các luật học và khả năng ứng dụng thực tế. Trong luận án này, nghiên cứu sinh phát triển một số thuật
toán học cho mạng nơ ron tế bào bậc cao (SOCeNNS) – dựa trên cấu trúc do Nguyễn Quang Hoan
và cộng sự đề xuất. Các thuật toán SORPLA, GA đề xuất có khả năng tính toán đầy đủ bộ trọng số
của SOCeNNs tuy nhiên để đảm bảo tính hội tụ của thuật toán, nghiên cứu sinh tiếp tục xây dựng
một thuật toán lai GASORPLA để đảm bảo tính hội tụ toàn cục bộ trọng số tính toán cho mạng nơ
ron tế bào bậc cao.
1. Đối tượng và phạm vi nghiên cứu
➢ Đối tượng nghiên cứu: Các luật học để xác định các bộ trọng số cho mạng nơ ron tế bào bậc
hai với cấu trúc đã chọn trước.
➢ Phạm vi nghiên cứu: Luận án giới hạn nghiên cứu các thuật toán hồi quy và phát triển thành
thuật toán dạng Perceptron (theo kiểu truyền thẳng) phù hợp cho mạng nơ ron tế bào bậc hai. Xây
dựng giải thuật di truyền để xác định bộ trọng số SOCeNNs và phương pháp học kết hợp giữa GA và
SORPLA để giảm thiểu các trường hợp tối ưu cục bộ của phương pháp SORPLA. Thử nghiệm cho
bài toán xác định biên ảnh sử dụng kết quả các thuật toán đã phát triển trong luận án chỉ để chứng tỏ
các bộ trọng số tìm được là đúng, đề xuất khả năng ứng dụng thực tế sau này. Trong nội dung nghiên
cứu tại luân án, NCS không đi sâu vào đánh giá chất lượng xử lý ảnh so với các phương pháp khác;
đây là một hướng nghiên cứu mà NCS sẽ định hướng vào giai đoạn tiếp theo.
2. Mục tiêu của luận án
Mục tiêu tổng quát: phát triển các luật học để xác định các bộ trọng số cho mạng nơ ron tế
bào bậc hai.
Mục tiêu cụ thể: Phát triển các luật học Perceptron hồi quy và thuật toán GA cho mạng nơ ron
tế bào bậc cao; Đề xuất thuật toán lai GASORPLA để tính toán bộ trọng số cho mạng nơ ron tế bào
bậc cao đảm bảo tối ưu toàn cục; Thử nghiệm kết quả các thuật toán trên mô phỏng và chương trình
phần mềm.
3. Phương pháp tiếp cận, nghiên cứu của luận án
Phương pháp tiếp cận: từ các tài liệu đã công bố, tham khảo các chuyên gia, mô hình toán học
và thực nghiệm;
Phương pháp nghiên cứu: kết hợp giữa nghiên cứu lý thuyết, các mô hình toán học, tiến hành
mô phỏng, thực nghiệm, đánh giá.
4. Nội dung nghiên cứu của Luận án
Bố cục của Luận án gồm ba chương:
Chương một. Trên cơ sở cấu trúc mạng nơ ron tế bào bậc hai, kết hợp với thuật toán Perceptron
hồi quy của C. Gukzelis và cộng sự, NCS đề xuất và phát triển luật học áp dụng cho mạng nơ ron tế
bào bậc hai để tính toán đầy đủ bộ trọng số SOCeNNs, chứng minh tính hội tụ của luật học đã đề
xuất.
Chương hai. Trên cơ sở cấu trúc mạng nơ ron tế bào bậc cao, kết hợp với thuật toán Perceptron
hồi quy của C. GuKzelis và cộng sự, nghiên cứu sinh đề xuất và phát triển luật học áp dụng cho mạng
nơ ron tế bào bậc cao để tính toán đầy đủ bộ trọng số SOCeNNs.
Chương ba. Dựa theo phương pháp đề xuất ở chương hai, NCS tiếp tục sử dụng giải thuật di

2
truyền xác định bộ trọng số cho mạng nơ rơn tế bào bậc hai, tiếp đó xây dựng thuật toán học lai giữa
GA kết hợp SORPLA để đảm bảo tính tối ưu toàn cục của thuật toán, đưa ra một số chứng minh về
khả năng xử lý ảnh của mạng nơ ron tế bào bậc hai.
Ở phần cuối đã trình bày một số kết luận về kết quả đạt được của luận án và kiến nghị hướng
nghiên cứu tiếp theo.
5. Đóng góp của luận án
Đóng góp thứ nhất: Phát triển luật học Perceptron hồi quy cho mạng nơ ron tế bào bậc hai
(SOCeNNs).
Đóng góp thứ hai: Chứng minh tính hội tụ của thuật toán SORPLA.
Đóng góp thứ ba: Xây dựng thuật toán GA cho mạng nơ ron tế bào bậc hai, và hai thuật toán
lai giữa GA với thuật toán RPLA và thuật toán SORPLA để cải thiện chất lượng học cho mạng nơ
ron tế bào bậc hai.
CHƯƠNG 1. TỔNG QUAN VỀ CẤU TRÚC
VÀ LUẬT HỌC MẠNG NƠ RON
1.1. Cấu trúc và luật học trong mạng nơ ron truyền thống
1.1.1. Khái niệm và phân loại học trong mạng nơ ron truyền thống
Học trong mạng nơ ron nhân tạo có thể chia làm hai loại: học cấu trúc và học tham số. Học cấu
trúc: xác định số lớp kết nối, số các phần tử nơ ron trong mỗi lớp. Học tham số: xác định bộ giá trị
trọng số trong mạng, được chia làm 03 loại:
Học không giám sát: Học từ các cặp mẫu đầu vào/ ra;
Học giám sát: Học từ các nhãn (gồm tín hiệu đầu vào, các đầu ra mong muốn). Nhãn đóng vai trò
như giáo viên nhằm giám sát quá trình học;
Học củng cố: Sử dụng các thông tin trái ngược nhau kết hợp các phản hồi thực tế để củng cố các
tín hiệu khác nhau.
1.1.2. Cấu trúc và luật học của mạng nơ ron truyền thẳng
1.1.2.1. Mạng Perceptron
Luật học Perceptron sử dụng phương pháp định tính : Thử - Sai – Chỉnh như trong học máy để xác
định bộ trọng số cho mạng có nhiều đầu ra.
( )
, , ,
,
1
1
2
0
=
= + − = = −
= − =
=
s
i
s s s s s
i j i j i j i j i i j
mi i i
ss
i i j j j
jii
w k w k w k e u k d y u k
d x khi d y
d sgn w u k u k khi d y
(1.1)
1.1.2.2. Mạng Adaline
Luật học Widrow-Hoff (hay luật học sai số bình phương tối thiểu: LMS) là luật học định lượng
và có sở cứ khoa học từ phương pháp hạ Gradient (Decent Gradient) từ viện nghiên cứu Massachusetts
(Hoa kỳ):
αE
wij wij
(1.2)
( ) ( )
,
1
'
=
= −
Ps s s s
i j i i i j
s
w d f x f x u
(1.3)
1.1.3. Cấu trúc và luật học mạng nơ ron bậc nhất hồi quy
1.1.3.1. Mạng Hopfield
❖ Cấu trúc mạng Hopfield
Năm 1982, Hopfield đề xuất mạng Hopfield rời rạc. Phương trình trạng thái của mạng như sau:

3
( ) ( )
,
j=1
t = y +
n
i i j j i
u w t I
với i, j = 1,2,…,n, I là ngưỡng (1.4)
Hopfield (1984) đưa ra mô hình mạng Hopfield liên tục được mô tả bằng tập phương trình vi
phân:
( )
n
j=1
= − + +
ii
i i, j j i
i
dx t x
C w y I
dt R
(1.5)
( )
=
j j j
y f x
(1.6)
( )
1−
=
i i i
x f y
(1.7)
❖ Ổn định mạng Hopfield
Hopfield sử dụng hàm
V(t)
thỏa mãn hai điều kiện để hàm V(t) là hàm Lyapunov và khi đó
hàm Lyapunov và mạng Hopfield liên tục ổn định theo tiêu chuẩn ổn định Lyapunov.
❖ Luật học mạng Hopfield
Luật cập nhật trọng số mạng Hopfield dựa theo luật Hebb tức là học không giám sát. Khi hàm
tương tác đầu ra là hàm dấu, trọng số của mạng Hopfiled được tính theo biểu thức như sau:
,
1
= =
=
−
W
T
Pss
ij nxn s
w Y Y PI
(1.8)
1.1.3.2. Mạng nơ ron tế bào chuẩn
a. Cấu trúc mạng nơ ron tế bào chuẩn
Năm 1998, L.O. Chua và L. Yang đề xuất mạng nơ ron tế bào (CeNNs). Bản chất của CeNNs là
hai mạng nơ ron Hopfield (nêu tại mục 1.1.3.1) được đưa vào hai hướng trở thành một ma trận đầu
vào (hay mảng). Khi đó, mạng nơ ron tế bào là một mảng các tế bào xử lý song song ở dạng tương
tự. Mỗi tế bào bao gồm các điện trở, tụ điện, các nguồn nuôi tuyến tính và phi tuyến.
Phương trình trạng thái của CeNNs:
( ) ( ) ( ) ( )
( )
( )
( )
,
, , ,
,,
1, ; , , ; ,= − + + +
ij
i j k l k l
k l k l
x
dx t
C x t A1 i j k l y t B1 i j k l u I
dt R
(1.9)
Phương trình đầu ra của mạng nơ ron tế bào như sau:
( ) ( ) ( )
( )
, , ,
111
2
= + − −
i j i j i j
y t x t x t
(1.10)
Phương trình đầu vào:
,,
=
i j i j
uE
(1.11)
Các điều kiện ràng buộc:
( )
,,
0 1; 1
i j i j
xu
(1.12)
Các điều kiện giả định (tính đối xứng):
( ) ( )
A1 i, j;k,l = A1 k,l;i, j
với
1 ;1
;
− + − +
i M j N
i r k i r j r k j r
(1.13)
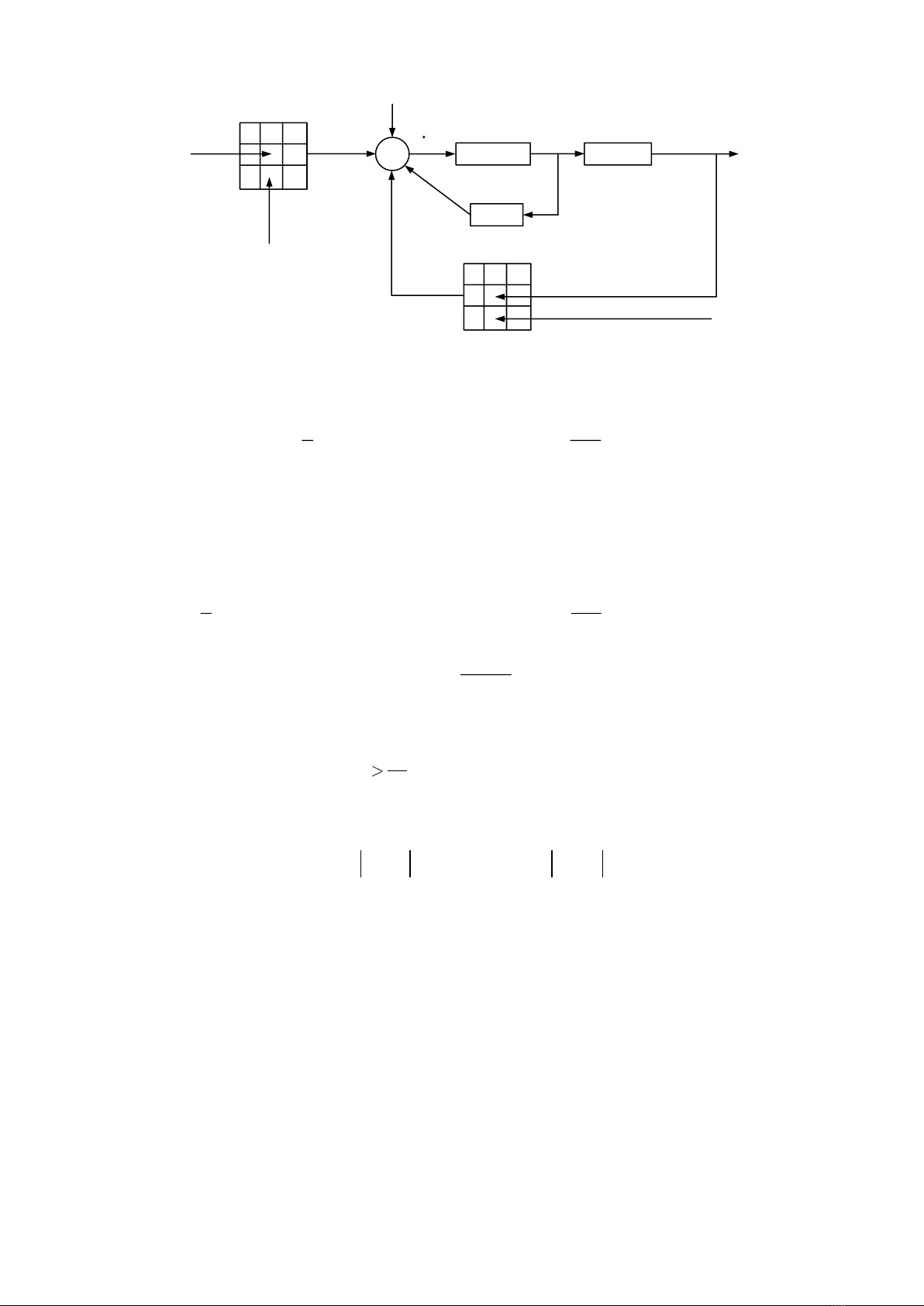
4
+Bộ tích phân f(x)
-1/Rx
Ma trận phản
hồi đầu ra
Phản hồi từ các lân cận
Ma trận điều
khiển đầu vào
Đầu vào Đầu ra
Đầu vào từ các lân cân
Ngưỡng
I
xx (t)
i,j y (t)
i,ji,j
u
Hình 1.1. Sơ đồ cấu trúc mạng nơ ron tế bào chuẩn
b. Tính ổn định của CeNNs:
Định lý 1.1: Cho hàm V(t):
( ) ( ) ( ) ( )
( )( )
( )
( )
( ) ( )
( )( )
( )
( )
2
, , ,
, , ,
, , ,
, , ,
11
= , ; ,
22
, ; ,
−+
−−
i j k l i j
i j k l i j
x
i j k l i j
i j k l i j
V t A1 i j k l y t y t y t
R
B1 i j k l y t u Iy t
(1.14)
thỏa mãn hai điều kiện:
1) hàm V( t) xác định dương và âm hay:
( )
||
max
t
max V t V
(1.15)
với:
( )
( )( )
( )
( )( )
1
2
max
i, j k,l i, j k,l x
1
V = | A1 i, j;k,l |+ | B1 i, j;k,l |+ MN +| I |
2R 0
(1.16)
2) đạo hàm của hàm V(t ) không dương, hay
( )
0
dt
dV t
(1.17)
thì hệ thống được mô tả theo các phương trình (1.9)-(1.13) ổn định đầy đủ.
Định lý 1.2: Nếu mạch điện tương ứng CeNNs thỏa mãn điều kiện:
1
x
A i, j;i, j R
(1.18)
thì sau quá trình quá độ, mỗi tế bào của CeNNs ổn định tại một điểm cân bằng. Khi đó, độ lớn của
điểm (trạng thái) cân bằng có giá trị tuyệt đối lớn hơn một, tức là:
( ) ( )
,,
lim 1;lim 1
→ →
= =
i j i j
tt
x t constant y t
(1.19)
c. Học trong mạng nơ ron tế bào:
Trong công bố về mạng nơ ron tế bào chuẩn, L. O. Chua giả định các tham số của ma trận
trọng số điều khiển
( )
, ; ,B1 i j k l
và ngưỡng I là các hằng số; còn các giá trị của ma trận trọng số phản
hồi
( )
, ; ,A1 i j k l
được tính theo luật học Hebb. Để tổng quát, bộ ma trận trọng số
( )
, ; ,B1 i j k l
và
ngưỡng I cũng cần phải dùng luật để tính. Hiện nay, nhiều phương pháp học được công bố để tính
các bộ trọng số
( )
, ; ,A1 i j k l
,
( )
, ; ,B1 i j k l
, và I. Một trong các phương pháp đó là biến đổi mạng
nơ ron tế bào có phản hồi (hay hồi quy) sang cấu trúc mạng truyền thẳng (các ma trận A1, B1, I được
ẩn bên trong và thay bằng một ma trận trọng số tổng W. Khi đó, mô hình cấu trúc mạng CeNNs
tương đương mạng Perceptron và có thể sử dụng luật học Perceptron để tính W. Ý tưởng và thuật
toán đó được C. Gukzelis đề xuất và gọi là thuật toán Perceptron hồi quy (RPLA).


























