Abstract: Nowadays, Performance Evaluation is one of
the most important fields of information technology. Hence,
it has been widely studied in recent years. This paper
presents the performance evaluation method using
Stochastic Petri Net. With the capability of simulating
complex systems and mapping to Markov chain, this
method is powerful widely used in many systems, especially
in computer and communication systems.
I. ĐẶT VẤN ĐỀ
Đánh giá hiệu năng thông qua mô phỏng hệ thống
là một phương pháp hiệu quả và đặc biệt hữu ích đối
với các nhà thiết kế, xây dựng hệ thống. Nền tảng của
phương pháp là:
− Mô phỏng hệ thống: mô hình hoá cấu trúc
(structure) và mô tả hành vi (behaviour) của hệ
thống.
− Phân tích, đánh giá hiệu năng trên mô hình mô
phỏng hệ thống.
Hiện nay, có ba phương pháp đánh giá hiệu năng
thông qua mô phỏng hệ thống [1], đó là: phương pháp
sử dụng Mạng hàng đợi (Queue Network - QN) [1,2],
phương pháp sử dụng Mạng Petri (Petri Net - PN) [3]
và phương pháp sử dụng Chương trình máy tính được
thiết kế đặc thù chỉ để mô phỏng cho một hệ thống [1].
Trong đó, phương pháp cuối cùng tuy cho kết quả với
độ tin cậy và chính xác cao nhưng phải trả giá về sự
đòi hỏi và chiếm dụng tài nguyên rất lớn, vì vậy,
phương pháp này thường ít được sử dụng trong đánh
giá hiệu năng. Phương pháp sử dụng mạng hàng đợi,
với nền tảng là lý thuyết xếp hàng và luật Little, do
chi phí thấp, việc mô phỏng đơn giản, trở nên rất hữu
dụng đối với các hệ thống không phức tạp, đòi hỏi độ
chính xác của kết quả phân tích không cao. Đối với
các hệ thống phức tạp do khả năng hạn chế trong việc
biểu diễn các quan hệ tương tranh (concurrency),
đồng bộ (synchronization) cũng như các hoạt động
nội tại của server nên phương pháp sử dụng mạng
hàng đợi không đáng tin cậy. Trong bối cảnh đó,
phương pháp sử dụng mạng Petri để mô phỏng hệ
thống, sau đó, trên cơ sở phân tích cây trạng thái
(được thể hiện thông qua tập hình trạng của mạng) để
rút ra các kết quả đánh giá hiệu năng cả về định tính
và định lượng, được coi như một giải pháp dung hoà
hai phương pháp trên, trong đó, kết hợp khả năng mô
phỏng phức tạp của phương pháp thứ ba với khả năng
phân tích đơn giản, hiệu quả của phương pháp đầu.
Phương pháp dùng mạng Petri có thể áp dụng đối với
các hệ thống có hoạt động phức tạp với đầy đủ các
mối quan hệ giữa các thành phần trong hệ thống.
Mô hình mạng Petri được Carl Adam Petri đề xuất
vào năm 1962, trải qua hơn 40 năm phát triển, từ một
mạng Petri đơn giản ban đầu, những người quan tâm
nghiên cứu đã cho ra đời một loạt các loại mạng Petri
mức cao (Coloured Petri Net, Predicate Petri Net,
Stochastic Petri Net...) có thể mô phỏng cũng như
phân tích hiệu năng cho các hệ thống từ đơn giản đến
phức tạp. Trong đó, mạng Stochastic Petri (SPN) [1,4]
do khả năng quy tương đương về chuỗi Markov đã tạo
ra một ưu thế vượt trội trong đánh giá hiệu năng định
lượng và trở thành một hướng nghiên cứu nhiều hứa
hẹn. PN nói chung và SPN nói riêng là những vấn đề
Phương pháp đánh giá hiệu năng hệ thống
sử dụng mạng Stochastic Petri
A System Performance Evaluation Method
Using Stochastic Petri Net
Tạ Hải Tùng
tương đối phức tạp, vì vậy, trong giới hạn ngắn gọn
của bài báo chúng tôi tập trung vào việc ứng dụng
SPN trong đánh giá hiệu năng, các khía cạnh chuyên
sâu có thể được tìm hiểu thêm trong các tài liệu tham
khảo [1,3,4,6].
II. PHƯƠNG PHÁP ĐÁNH GIÁ HIỆU NĂNG
HỆ THỐNG SỬ DỤNG MẠNG STOCHASTIC
PETRI
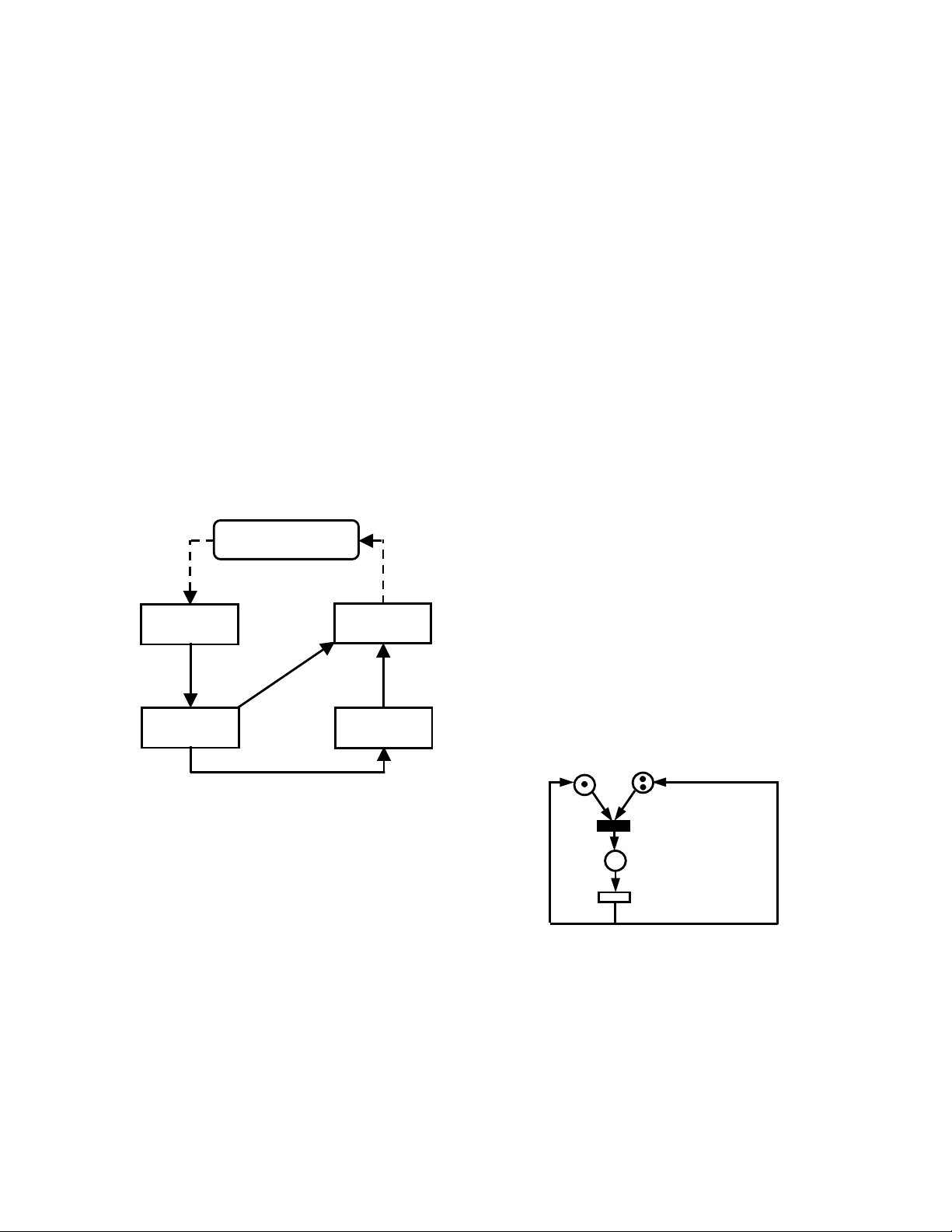
Hình1 chỉ rõ các bước của phương pháp (mỗi bước
ứng với một cung, bước tương ứng với cung đứt nét
có thể được thực hiện nhiều lần để mang lại kết quả
tối ưu):
Bước 1: Mô phỏng hệ thống thành một SPN.
Bước 2: Xây dựng cây trạng thái của hệ thống
thông qua việc xây dựng tập hình trạng của SPN.
Bước 3: Tiến hành phân tích hiệu năng định tính.
Hình 1: Sơ đồ ứng dụng SPN trong đánh giá hiệu năng
Bước 4: Trên cơ sở cây trạng thái, xây dựng chuỗi
Markov thời gian liên tục (Continuous Time Markov
Chain - CTMC) đại diện cho hệ thống.
Bước 5: Tiến hành phân tích hiệu năng định lượng.
Bước 6: Từ kết quả đánh giá hiệu năng tiến hành
xây dựng hệ thống (bước này không được đề cập do
ngoài phạm vi bài báo).
Các mục tiếp sau sẽ đi vào cụ thể của từng bước.
1. Mô phỏng hệ thống về SPN
a) SPN
Mô hình SPN là một đồ thị có hướng. Trong đó các
đỉnh là: các place đại diện bởi các hình tròn, các
transition đại diện bởi các hình chữ nhật: hình chữ
nhật đen là transition tức thời (immediate transition –
i-transition), hình chữ nhật trắng là các transition gắn
thời gian (timed transition – t-transition). Các đỉnh
khác loại nối với nhau bởi các cung, đối với đỉnh là
transition tương ứng có các cung vào (input arc), cung
ra (output arc), cung ức chế (inhibitor arc) phân biệt
bởi đoạn thằng có hình tròn ở đầu. Mỗi place có chứa
các token, được biểu diễn bởi các hình tròn đen (do
vấn đề ngữ nghĩa nên trong bài báo này vẫn sử dụng
nguyên gốc các thuật ngữ: place, transition, token).
Một sự phân bố các token tại mỗi place là một hình
trạng (marking) của SPN
Về mặt hình thức, SPN được định nghĩa như sau:
Định nghĩa 1: Một SPN được biểu diễn bởi:
SPN = (P, T, Pr, I, O, H, W, m0)
Trong đó: P: tập các place (|P| = np).
T: là tập các transition (|T| = nt).
Pr: tập ưu tiên gắn với mỗi transition. Với lưu ý một i-
transition luôn có giá trị ưu tiên lớn hơn bất kỳ một t-
transition nào.
I, O, H: Các tập trọng số tương ứng với cung vào, cung
ra, cung ức chế.
W:T
→
R+ là một hàm liên kết với mỗi transition t. Đối
với t-transition thì W(t) là tốc độ kích hoạt (firing rate).
P
m
Nm ∈
0 là hình trạng ban đầu.
Hình 2: Mạng Stochastic Petri
Trong hình 2:
P = {p1,p2,p3}; T = {t1,t2}; m0 = (1,2,0)
Nét đặc thù của SPN là sự liên kết yếu tố thời gian
(tuân theo phân bố xác suất mũ) với sự kích hoạt của
t-transition trong SPN thông qua tốc độ kích hoạt W(t-
Bộ nh
ớ
p2
t2 CPU kết thúc
xử lý lệnh
t1 CPU bắt đầu
xử lý lệnh
p3 CPU đang xử lý
lệnh
CPU sẵn sàng
p1
Mô phỏng
(1)
Xây dựng
cây
trạng thái
(
2
)
Phân tích
định lượng
(5)
Phân tích
định tính
(3)
Diễn giải,
xây dựng
hệ thống
(6)
Xây dựng CTMC
(4)
Hệ thống mong đợi
SPN
Cây trạng thái CTMC
Kết quả đánh
g
iá hi
ệ
u năn
g
transition).
Ngoài các thành phần cơ bản trên, hiện nay để mô
phỏng các hệ thống phức tạp, người ta còn thêm vào
một số thành phần mở rộng tạo nên mạng Stochastic
Reward (SRN) [6,7]
− Ý nghĩa các thành phần của SPN trong mô phỏng hệ
thống:
Place: Đại diện cho tài nguyên hay tình trạng của
tài nguyên.
Transition: Đại diện cho một sự kiện trong chuỗi sự
kiện xảy ra trong quá trình hoạt động của hệ thống.
i-transition: Đại diện cho sự kiện xảy ra tức thời khi
mà điều kiện kích hoạt được thoả mãn.
t-transition: Đại diện cho sự kiện cần trải qua thời
gian trễ trước khi kích hoạt.
Cung: Đại diện cho luồng vào và luồng ra của hệ
thống.
Token: Bản thân token không có ý nghĩa bằng số
lượng token. Số lượng token đại diện cho số lượng tài
nguyên, số lượng yêu cầu... Số lượng token kết hợp
với các place và các cung cấu thành điều kiện để kích
hoạt một transition (cấu thành một sự kiện). Sự lưu
chuyển token thể hiện hoạt động của hệ thống. Sự
phân bố các token đại diện cho các trạng thái của hệ
thống.
Xuất phát từ ý nghĩa trên chúng ta thấy được rằng:
− Cấu trúc của hệ thống có thể được mô phỏng bởi sự
biểu diễn về mặt hình học các thành phần của SPN
(place, transition, token, cung).
− Hoạt động của hệ thống có thể được mô phỏng bởi
sự lưu chuyển các token (chính là sự biến đổi các
trạng thái của hệ thống) giữa các đỉnh của SPN
thông qua sự kích hoạt của các transition (hay sự
xuất hiện của các sự kiện). Đây chính là quá trình
mô tả hành vi trong mô phỏng hệ thống.
Định nghĩa 2: Một transition t gọi là có khả năng
kích hoạt (enabled) trong một hình trạng m khi mà
mọi place đầu vào của t chứa số token không nhỏ hơn
trọng số của cung liên kết và mọi place đầu vào ức
chế có số lượng token nhỏ hơn trọng số của cung ức
chế liên kết.
Định nghĩa 3: Hình trạng m tồn tại một i-transition
có khả năng kích hoạt được gọi là hình trạng vô hình
(vanishing marking). Ngược lại, ta có hình trạng hữu
hình (tangible marking).
Một transition có khả năng kích hoạt t được chọn
kích hoạt sẽ trải qua một khoảng thời gian trễ tuân
theo phân bố hàm mũ (nếu là i-transition thì thời gian
trễ bằng 0) trước khi kích hoạt. Khi kích hoạt, t sẽ loại
khỏi các place vào (kết nối với t thông qua cung vào)
số lượng token tương ứng với trọng số của cung liên
kết và đưa ra place ra (kết nối với t thông qua cung
ra) số token tương ứng với trọng số của cung liên kết.
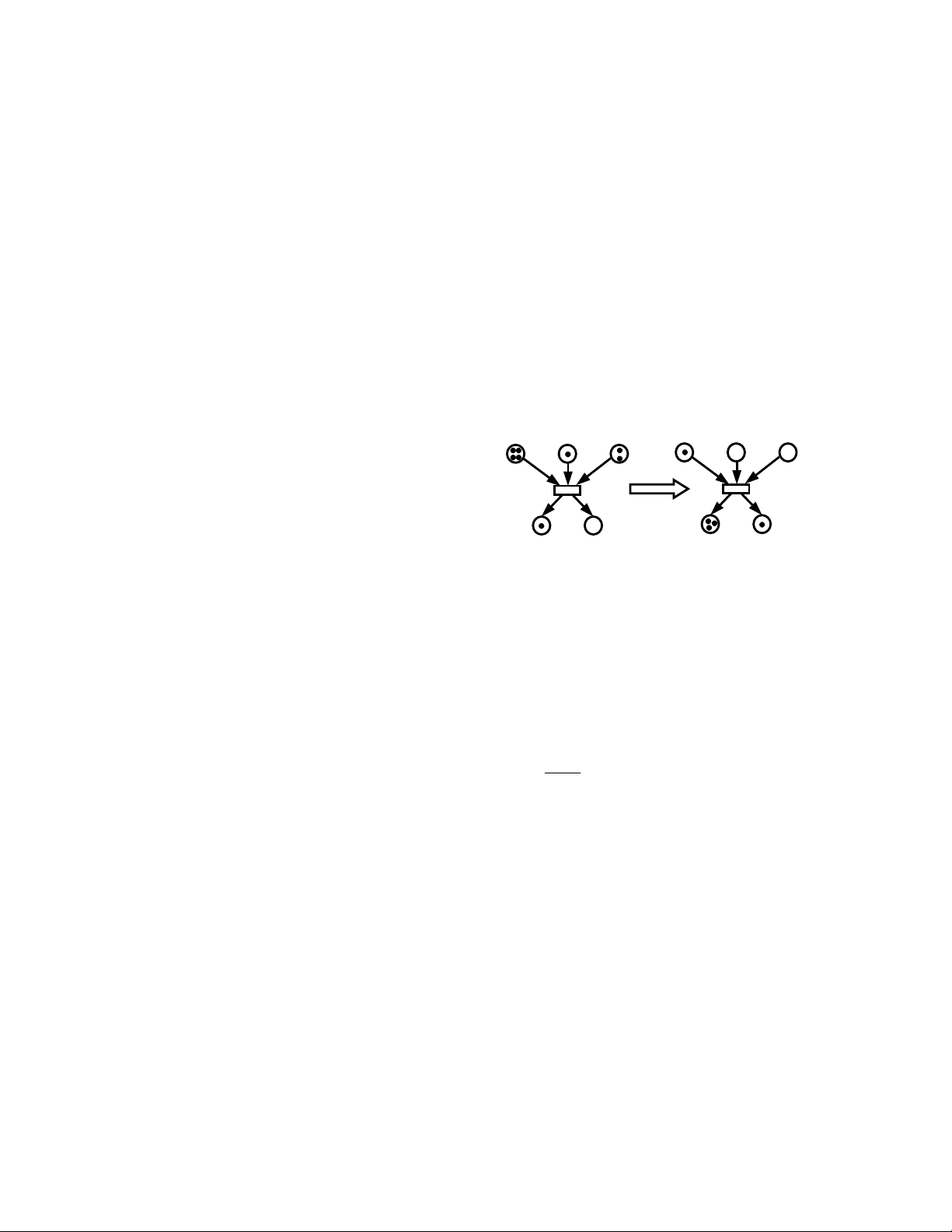
Trong hình 3 , chúng ta sẽ xem xét sự biến đổi hình
trạng của SPN khi kích hoạt t.
Hình 3: Sự lưu chuyển token trong SPN
Khi trong một hình trạng có nhiều hơn một
transition có khả năng kích hoạt thì luật sau sẽ được
áp dụng để chọn ra một transition được kích hoạt [4]:
Một transition trong số các i-transition có khả năng
kích hoạt (nếu tồn tại) sẽ được chọn đầu tiên theo xác
suất: W
W(t)
=p. Với W là tổng độ phức tạp của các
i-transition có khả năng kích hoạt.
Nếu không tồn tại i-transition có khả năng kích
hoạt, một t-transition sẽ được chọn theo một trong hai
chiến lược:
1. Chiến lược “chạy đua” (race policy)
Trong chiến lược này thì t-transition nào có tốc độ
lớn nhất (hay thời gian trễ nhỏ nhất) trong số các t-
transition có khả năng kích hoạt sẽ được chọn kích
hoạt trước. Chính vì vậy, nảy sinh một vấn đề: So
sánh thời gian trễ giữa các t-transition có gốc thời gian
khác nhau. Trong bối cảnh đó có hai phương pháp:
− Phương pháp khởi tạo lại từ đầu (resampling): Khi
2
2
3
t
(b)
M’ = (1,0,0,3,1)
(a)
M = (4,1,2,1,0)
kích hoạt t
2
2
3
t
xét chọn transition kích hoạt thì đồng thời khởi tạo
lại gốc thời gian đối chứng. Nghĩa là không hề xét
đến các yếu tố lịch sử.
− Phương pháp nhớ (memory policy) được bổ sung
thêm vào chính sách để lưu lại các thông tin lịch sử
kích hoạt, phương pháp nhớ gồm các phương pháp
con sau:
Phương pháp nhớ mức thấp: Trong phương pháp
này, tại hình trạng hiện tại, nếu transition ti vẫn tiếp
tục giữ khả năng kích hoạt có được từ các nhịp trước
nhưng tại đó không được chọn kích hoạt thì sẽ không
phải khởi tạo lại gốc thời gian khi đem so sánh với các
transition có khả năng kích hoạt khác.
Phương pháp nhớ mức cao: Phương pháp này,
ngoài khả năng lưu vết các transition vẫn tiếp tục giữ
khả năng kích hoạt, còn có khả năng lưu vết một
transition khi nó không có khả năng kích hoạt ở nhịp
sau, để đến khi nó lại có khả năng này ở một nhịp nào
đó trong tương lai thì gốc thời gian không phải khởi
tạo lại.
2. Chiến lược lựa chọn trước (preselection policy)
Trong đó t-transition sẽ được chọn với xác suất
W
W(t)
=p. Với W là tổng tốc độ kích hoạt của các t-
transition có khả năng kích hoạt.
b) Các bước mô phỏng hệ thống
Bước 1: Xác định các hoạt động, chuỗi sự kiện của
hành động và tài nguyên cần thiết cho quá trình hoạt
động của hệ thống.
Bước 2: Sắp đặt các hoạt động theo mối quan hệ
nhân quả xác định trước (hoạt động nào kéo theo
hoạt động nào)
Bước 3: Mỗi hoạt động hoặc sự kiện sẽ được đại
diện bởi một transition.
Bước 4: Các tài nguyên cần thiết, các trạng thái
trải qua trong quá trình hoạt động của tài nguyên
được đại diện bởi các place.
Bước 5: Xác định hình trạng ban đầu của hệ thống.
Bước 6: Chọn lựa chiến lược hoạt động (một trong
hai chiến lược: chạy đua hay lựa chọn trước)
2. Xây dựng cây trạng thái
Cây trạng thái của hệ thống được thể hiện thông
qua tập hình trạng của SPN, với mỗi hình trạng đại
diện cho một trạng thái. Gọi:
RS (Reachability Set) là tập hình trạng của hệ
thống.
NM (New Marking) là tập hình trạng mới chưa
được xét.
Et(m) là tập các transition có khả năng kích hoạt tại
hình trạng m.
Ta có thuật toán xây dựng cây trạng thái với tư
tưởng của thuật toán là: Xuất phát từ hình trạng ban
đầu, ta xác định các transition có khả năng kích hoạt
(chính là các sự kiện có thể xảy ra trong hệ thống), lần
lượt kích hoạt các transition để tạo ra các hình trạng
mới (trạng thái mới của hệ thống), đồng thời lưu trữ
các thông tin về phép chuyển đổi hình trạng đó để tạo
ra ma trận Q' (với m, m' là chỉ số hàng và cột, W(t,m)
là giá trị của phần tử tương ứng). Công việc được tiếp
tục lặp lại với các hình trạng mới (theo nghĩa không
có trong tập các hình trạng đã có), đến khi không thể
nảy sinh ra một hình trạng mới nào.
1. input {P,T,PR,I,O,H,W,m0}
2. NM := {m0}; RS := {m0}
3. while NM
≠
∅
4. begin
5. let m
∈
NM
6. NM := NM - {m}
7. for all t
∈
Et(m)
8. begin
9. let m
→
t m'
10. store_Q’(m,m',W(t,m))
11. if m'
∉
RS
12. then NM := NM
∪
{m'}
13. RS := RS
∪
{m'}
14. else mark(m’)
15. end
16. end
17. p(0) = (1,0,...,0)
18. Output RS,Q’,p(0)
Với đầu vào là SPN trải qua thuật toán trên chúng ta
thu được tập hình trạng của SPN, đồng thời thu được
ma trận Q’ có số chiều bằng số trạng thái trong hệ
thống và xác suất thời điểm ban đầu p(0) phục vụ cho
quá trình xây dựng CTMC sau này.
Thuật toán trên chỉ dừng khi số lượng trạng thái của
hệ thống là hữu hạn. Đối với các hệ thống mà việc
xuất hiện các trạng thái mới là vô hạn thì cây trạng
thái cũng có số nút không thể xác định được và thuật
toán không dừng, đó chính là hiện tượng bùng nổ
trạng thái (state explosion). Phương pháp đánh giá
hiệu năng đề cập trong bài báo này chỉ quan tâm đến
các hệ thống hữu hạn trạng thái.
3. Phân tích hiệu năng định tính
Phân tích hiệu năng định tính đem lại câu trả lời về
các tính chất, thuộc tính của hệ thống. Dưới đây sẽ
định nghĩa một số thuộc tính tiêu biểu của hệ thống
cũng như cách phân tích nó trong SPN.
a) Tính dừng
Định nghĩa 4: Hệ thống được gọi là dừng nếu trong
quá trình hoạt động hệ thống đạt tới “điểm chết”
(deadlock) (điểm tại đó không có sự kiện tiếp theo xảy
ra và hệ thống sẽ giữ trạng thái mà nó đạt được đến
khi nào có tác động của môi trường bên ngoài).
Ngược lại ta có hệ thống “sống” (live)
Tính chất này được phân tích trong SPN dựa vào
tập hình trạng của hệ thống: Nếu tồn tại hình trạng
không có khả năng kích hoạt một transition nào, ta kết
luận: hệ thống dừng.
b) Tính giới hạn (Bounded)
Định nghĩa 5: Một hệ thống được gọi là giới hạn
nếu số lượng trạng thái của nó là giới hạn.
Trong SPN, khái niệm giới hạn được gắn với số
lượng token tại mỗi place: Nếu tồn tại một place có số
lượng token tăng lên không ngừng vượt quá một giới
hạn định trước thì coi hệ thống là không giới hạn. Nếu
hệ thống có số lượng token tại mỗi place luôn nhỏ hơn
một số k thì hệ thống được gọi là k-bounded.
c) Tính bảo toàn (Conservative)
Định nghĩa 6: Một SPN được coi là bảo toàn nếu
số lượng token tại mọi hình trạng trong tập hình trạng
của nó là như nhau.
d) Tính khôi phục ngược (Reversible)
Định nghĩa 7: Hệ thống được gọi là có khả năng
khôi phục ngược nếu trong quá trình hoạt động có khả
năng quay lại trạng thái ban đầu.
Trong SPN, tính chất này sẽ được phân tích thông
qua việc tìm kiếm hình trạng ban đầu tại các node
khác node gốc của tập hình trạng.
4. Xây dựng CTMC
CTMC – Continuous Time Markov Chain – được
xác định theo quan hệ sau:
Pr{Xn+1=xn+1/Xn=xn,...,X0=x0} = Pr{Xn+1=xn+1/Xn=xn} (1)
Với Xi∈
Τ
là trạng thái tại thời điểm ti,
Τ
là tập
trạng thái, t0<t1<...<tn+1. Do thời gian là liên tục mà
không gian trạng thái lại rời rạc, nên khi đạt đến một
trạng thái thì CTMC sẽ “ở” trạng thái đó trong một
khoảng thời gian gọi là thời gian trễ (residence time)
tuân theo phân bố xác suất mũ với hàm phân bố:
)2(0,1)( ≥−= −tetF t
i
i
µ
Vì vậy một CTMC được đại diện bởi ma trận Q và
véc-tơ xác suất thời điểm ban đầu p(0), trong đó, các
phần tử của ma trận Q chính là thành phần tốc độ (
µ
i)
dùng để xác định thời gian trễ tại mỗi trạng thái i
trong (1).
Trong SPN do yếu tố thời gian được gắn với t-
transition nên các phần tử của ma trận Q lúc này chính
là tốc độ kích hoạt của t-transition. Q được xây dựng
từ Q' sau khi đã loại các phần tử tương ứng với các
hình trạng (trạng thái) vô hình (định nghĩa 3) (do
trạng thái này thực tế không tồn tại, hệ thống sẽ ngay
lập tức chuyển sang trạng thái hữu hình kế tiếp). Cơ
sở để xây dựng Q được mô tả thông qua hình 4:
Hình 4: Xây dựng ma trận đặc trưng Q từ cây trạng thái
Trong đó: 1 và 3 là các trạng thái hữu hình, 2 là
trạng thái vô hình
21
1
t
→ với t1 là t-transition với tốc độ kích hoạt
µ
1.
λ
Q =
µ
2
µ
1
1
3
2
-
µ
1
µ
2
µ
1
µ
2
λ
-
λ