TR NG THPT HÙNG V NG SÁNG KIÉN KINH NGHI MƯỜ ƯƠ Ệ
NĂM H C 2011-2012 GV TRÁC TH HU NH LIÊNỌ Ị Ỳ
1
SÔÛ GIAÙO DUÏC ÑAØO TAÏO BÌNH PHÖÔÙC
TRÖÔØNG THPT HUØNG VÖÔNG
SAÙNG KIEÁN KINH NGHIEÄM
MOÂN TOAÙN
ÑEÀ TAØI:M T S PH NG PHÁPỘ Ố ƯƠ
H NG D N H C SINH H C T TƯỚ Ẫ Ọ Ọ Ố
QUAN H VUÔNG GÓC TRONG HÌNHỆ
H C KHÔNG GIANỌ
GV : TRAÙC THÒ HUYØNH LIEÂN
GV : TRAÙC THÒ HUY ØNH LIEÂN
NAÊM HOÏC 2011 - 2012
TR NG THPT HÙNG V NG SÁNG KIÉN KINH NGHI MƯỜ ƯƠ Ệ
A/ PHAÀN MÔÛ ÑAÀU
I/ LYÙ DO CHOÏN ÑEÀ TAØI :
Trong quá trình d y toán b c THPT tôi nh n th y đa s h c sinh r t e ng i bàiạ ở ậ ậ ấ ố ọ ấ ạ
toán hình h c không gian, tình tr ng này có nhi u lý doọ ạ ề :
1/ Đ h c t t phân môn HHKG đòi h i ng i h c ph i có t duy nh i bén, ócể ọ ố ỏ ườ ọ ả ư ạ
t ng t ng phong phú, ph i n m đc các qui c v hình. Nh ng hi n nay đa sưở ượ ả ắ ượ ướ ẽ ư ệ ố
h c sinh l i l i t duy, ít suy nghĩ, bài toán nào h i khó là b qua không kiên trì ọ ạ ườ ư ơ ỏ
tìm ki m ph ng pháp gi i.ế ươ ả
2/ Phân môn HHKG đc h c ph n c b n l p 11 và ph n t ng h p l p 12.ượ ọ ầ ơ ả ở ớ ầ ổ ợ ở ớ
Do đó đa s h c sinh không chú ý, không n m v ng v n đ c t lõi c a ch ng trìnhố ọ ắ ữ ấ ề ố ủ ươ
l p 11, không rèn luy n k năng gi i toán t l p 11 nên khi lên l p 12 h u h t các ớ ệ ỹ ả ừ ớ ớ ầ ế
em đu s ph n HHKG này.ề ợ ầ
M t khác trong đ thi t t nghi p THPT và đ thi ĐH luôn có m t bài toán HHKGặ ề ố ệ ề ộ
ph n b t bu c,ở ầ ắ ộ vì v y ậđeå giuùp caùc em hoïc sinh làm t t h n bài toán HHKGố ơ
trong
các kỳ thi toâi maïnh daïn vieát ñeà taøi naøy.N i dung đ tài này tôi ch g i ý m t vàiộ ề ỉ ợ ộ
d ng toán ch l c và ph ng pháp gi i đ t đó h c sinh v n d ng vào gi i đạ ủ ự ươ ả ể ừ ọ ậ ụ ả ề
toán trong các k thi.ỳ
Tôi raát mong nhaän ñöôïc yù kieán ñoùng goùp chaân thaønh cuûa quí thaày coâ
cuøng
ñoàng nghieäp ñeå baøi vieát ñöôïc toång quaùt hôn, hay hôn
II/ NỘI DUNG :
Bài vi t g m các ph n sau:ế ồ ầ
1/ Cách xác đnh đo n vuông góc h t m t đi m đn m t m t ph ng. T d ngị ạ ạ ừ ộ ể ế ộ ặ ẳ ừ ạ
toán này h c sinh tính đc kho ng cách t m t đi m đn m t m t ph ng, kho ngọ ượ ả ừ ộ ể ế ộ ặ ẳ ả
cách t m t đng th ng đn m t m t ph ng song song v i nó, kho ng cách gi a ừ ộ ườ ẳ ế ộ ặ ẳ ớ ả ữ
hai m t ph ng song song, kho ng cách gi a hai đng th ng chéo nhau, tính góc ặ ẳ ả ữ ườ ẳ
gi a đng th ng và m t ph ng.ữ ườ ẳ ặ ẳ
2/ Cách v m t ph ng ẽ ặ ẳ qua M vaø song song với hai đng th ng a và b cho tr cườ ẳ ướ ,
tìm thieát dieän.
Từ d ng toán này h c sinh ạ ọ v đc ẽ ượ maët phaúng qua M và song song với maët
phaúng
cho tr cướ , v đc ẽ ượ maët phaúng qua M và vuông góc với đng th ng a cho tr c,ườ ẳ ướ
v đc ẽ ượ maët phaúng chöùa ñöôøng thaúng a vaø vuông góc với maët phaúng cho
tr cướ .
Đng Xoài, ngày 26 tháng 1 năm 2012ồ
Giáo viên
NĂM H C 2011-2012 GV TRÁC TH HU NH LIÊNỌ Ị Ỳ
2
TR NG THPT HÙNG V NG SÁNG KIÉN KINH NGHI MƯỜ ƯƠ Ệ
TRÁC TH HU NH LIÊNỊ Ỳ
B/ PHAÀN NOÄI DUNG
D ạ ng 1 : Caùch xaùc ñònh ñoïan vuoâng goùc haï töø ñieåm M ñeán maët
phaúng (
)
TH1 : Ta có đnh lýị : « Neáu từ M coù caùc ñoïan xieân daøi baèng nhau thì hình chieáu cuûa
chuùng
phải baèng nhau và ng c l iượ ạ », căn c vào đnh lý này ta xác đnh chân đng vuông góc h t ứ ị ị ườ ạ ừ
đi m M ể
TH2 : Neáu từ M khoâng coù caùc ñoïan xieân daøi baèng nhau thì :
+ Choïn maët phaúng
)(
qua Mvaø (
)
)(
+ Tìm c = (
)
)(
+ Töø M haï ñöôøng vuoâng goùc MH ñeán ñöôøng giao tuyeán c
)(
MH
Ứng dụng 1 : Kho ng cách t đi m M đn ả ừ ể ế maët phaúng (
): là đ dài MHộ
Gi i:ả
Nh n xét:ậDo SA = SB = SC nên bài toán này thu c TH1ộ
G i H là hình chi u vuông góc c a S trên m t ph ng (ABC)ọ ế ủ ặ ẳ
Do SA = SB = SC nên HA = HB = HC
H là tâm đng tròn ngo i ti p tam giác ABCườ ạ ế
Do tam giác ABC đu nên H là tr ng tâm tam giác ABCề ọ
d( S, (ABC)) = SH
Ta có HA =
Xét tam giác SAH:
2 2
SH SA AH a= − =
VSABC =
1.
3
ABC
S SH
=
3
3
12
a
b/
( )
( )
( )
ﾷ
, ,SA ABC SA AB SAH= =
cos
ﾷ
SAH
=
ﾷ
0
160
2
AH SAH
SA = =�
T cách xác đnh TH1 ta đi đn m t nh n xét cho hình chóp đa giác đu:ừ ị ở ế ộ ậ ề
“ Trong hình chóp đa giác đu thì hình chi u vuông góc c a đnh trên m t ph ng đáy ph i trùng ề ế ủ ỉ ặ ẳ ả
v i ớ
NĂM H C 2011-2012 GV TRÁC TH HU NH LIÊNỌ Ị Ỳ
3
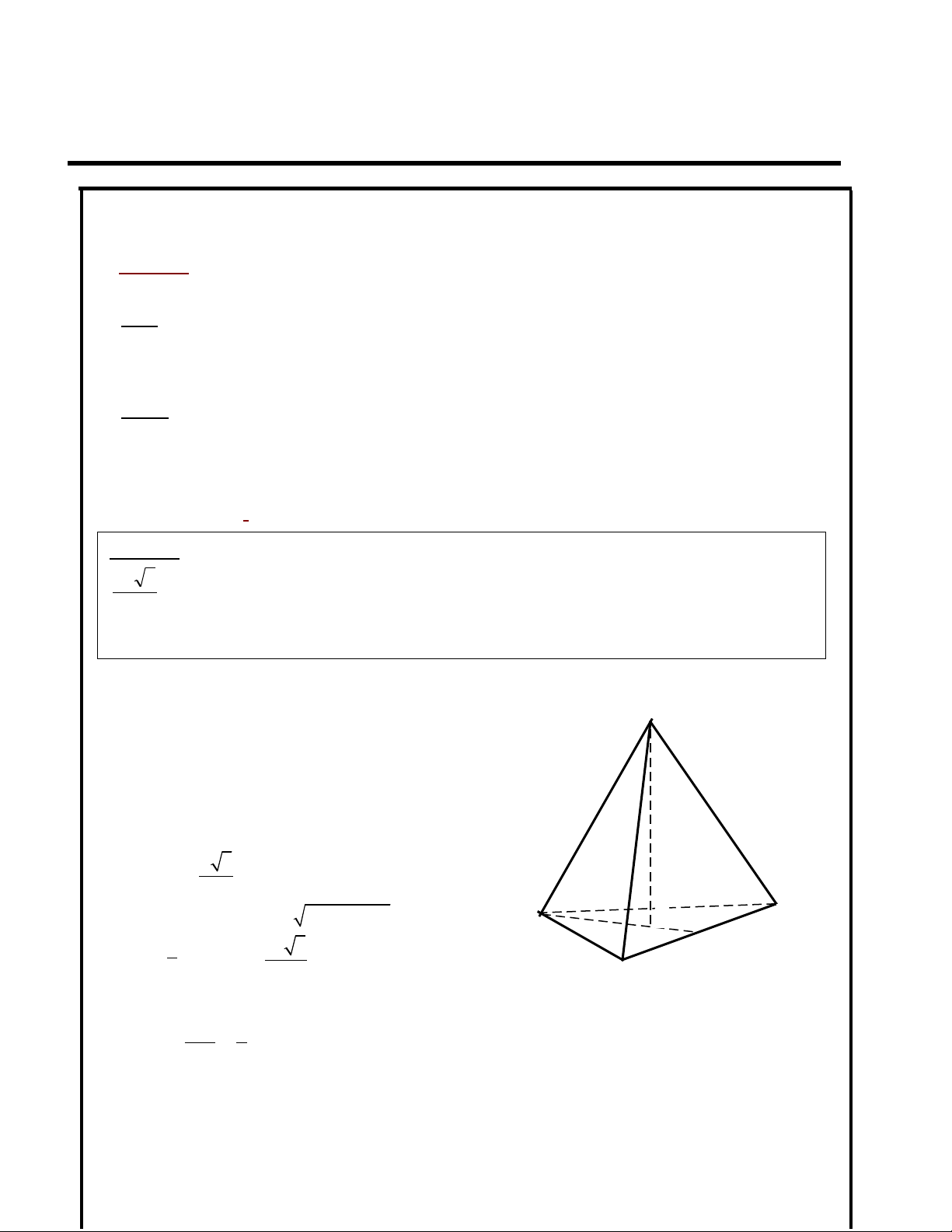
Ví duï 1: Cho hình choùp S.ABC coù ABC laø tam giaùc ñeàu caïnh a , SA =
SB = SC =
3
32a
a/ Tính khoaûng caùch töø S ñeán maët phaúng (ABC) ?
b/ Tính goùc giöõa SA vaø maët phaúng ( ABC) ?
S
A
B
C
H
TR NG THPT HÙNG V NG SÁNG KIÉN KINH NGHI MƯỜ ƯƠ Ệ
tâm c a đng tròn ngo i ti p đa giác đáy”ủ ườ ạ ế
Nh n xétậ Vì S.ABCD là hình chóp đu nên hình chi u c a S trên m t ph ng (ABCD) ph i trùng ề ế ủ ặ ẳ ả
v i ớ
tâm đng tròn ngo i ti p hình vuông ABCD .T đó ta có cách v hình nh sau:ườ ạ ế ừ ẽ ư
* B c 1: V hình vuông ABCD, l y giao đi m hai đng chéo là Oướ ẽ ấ ẻ ườ
* B c 2: T O d ng đng vuông góc v i m t ph ng (ABCD), ch n đnh S khác O trên đng ướ ừ ự ườ ớ ặ ẳ ọ ỉ ườ
vuông góc này
* B c 3: N i S v i các đnh A, B, C, D ta đc hình chóp S.ABCDướ ố ớ ỉ ượ
Gi i:ả
Vì S.ABCD là hình chóp đu nên SO ề
⊥
(ABCD) v i O = ACớ
BD
VSABCD =
1.
3
ABCD
S SO
SABCD = a 2
Xét tam giác SAO vuông t i O có SA = ạa
2
,
OA =
1 1 2
2 2
AC a=
2
2 2 2
3
222
a a
SO SA OA a= − = − =�
V y ậ
3
2
1 3
.
32 6
SABCD
a a
V a= =
Gi i:ả
1/ Nh n xét : ta c n xác đnh đo n vuông góc h t D ậ ầ ị ạ ạ ừ
đn m t ph ng ( ABC)ế ặ ẳ
DB = DC = a, DA = a
2
( xét tam giác ABD vuông t i B)ạ
ta tìm hai m t ph ng vuông góc nhau trong đó có m t ặ ẳ ộ
m t ph ng đi qua Dặ ẳ
Ta có :
AB
⊥
(BCD)
(ABC)
⊥
(BCD)
NĂM H C 2011-2012 GV TRÁC TH HU NH LIÊNỌ Ị Ỳ
4
Ví duï 3: Cho tø diÖn ABCD cã BCD lµ tam gi¸c ®Òu c¹nh a, AB
(BCD)
vµ AB = a. TÝnh kho¶ng c¸ch:
A
B
C
D
MH
K
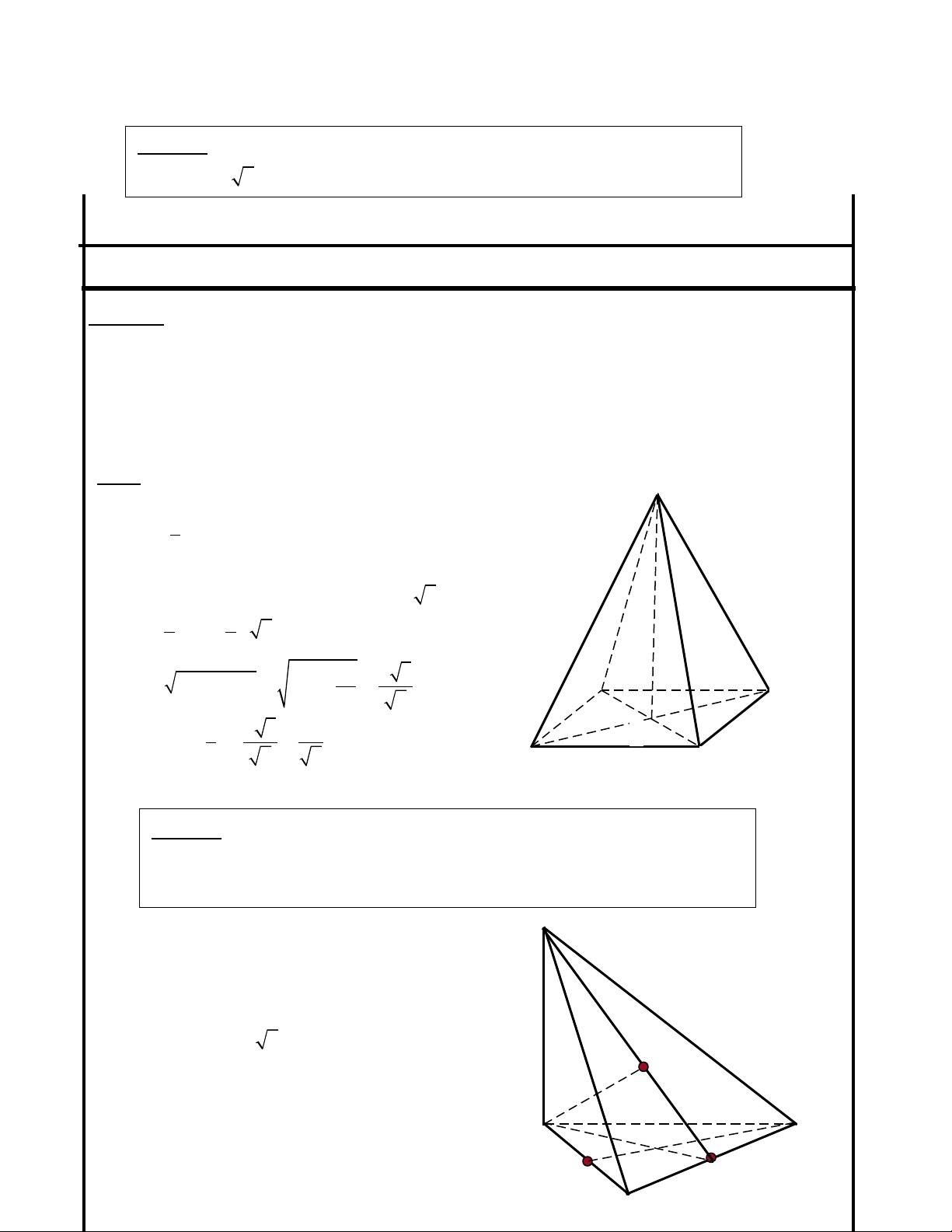
Ví duï 2: Cho hình chóp t giác đu S.ABCD có c nh đáy b ng a, c nhứ ề ạ ằ ạ
bên b ng aằ
2
,Tính th tích kh i chóp đu S.ABCD ể ố ề
S
A
B
C
D
O
TR NG THPT HÙNG V NG SÁNG KIÉN KINH NGHI MƯỜ ƯƠ Ệ
Mà (ABC)
(BCD) = BC
K DH ẻ
⊥
BC
DH
⊥
( ABC)
V y kho ng cách t D đn (ABC) là DH = aậ ả ừ ế
3
2
( do DH là đng cao trong tam giác đu BCD)ườ ề
2/ Tính d( B,(ACD))?
Cách 1 : G i M là trung đi m CD, ta cóọ ể :
( )
, ( )
BM CD
AB CD CD ABM
BM AB ABM
⊥s
⊥ ⊥�
�
(ACD)
⊥
(ABM)
Mà (ABM)
(ACD) = AM
K BK ẻ
⊥
AM
BK
⊥
( ACD)
V y kho ng cách t B đn (ACD) là BKậ ả ừ ế
Xét tam giác ABM vuông t i Bạ
2 2 2 2 2 2
1 1 1 1 4 7
3 3BK BA BM a a a
= + = + =
d( B,(ACD)) = BK =
Cách 2 : Nh n xét : ta có BA = BC = BD = a ậ
n u K là hình chi u vuông góc c a B trên (ACD) ế ế ủ
thì KA = KC = KD
K là tâm đng tròn ngo i ti p tam giác ACDườ ạ ế
Do AC = AD = a
2
nên K n m trên AM, tính BK = ằ
Ứng d ụng 2 : Kho ng cách t đng th ng a đn ả ừ ườ ẳ ế ma ët pha ún g (
)
song song v i aớ
Gi i:ả
1/ Tính d(B,(SCD)) ?
Nh n xét : T B ta không có các đo n xiên b ng nhau đn ậ ừ ạ ằ ế
m t ph ng (SCD) và cũng không tìm đc m t m t ph ng ch a ặ ẳ ượ ộ ặ ẳ ứ
B và vuông góc v i (SCD), nh ng B n m trên c ng AB và ớ ư ằ ạ
AB//CD nên AB//(SCD)
NĂM H C 2011-2012 GV TRÁC TH HU NH LIÊNỌ Ị Ỳ
5
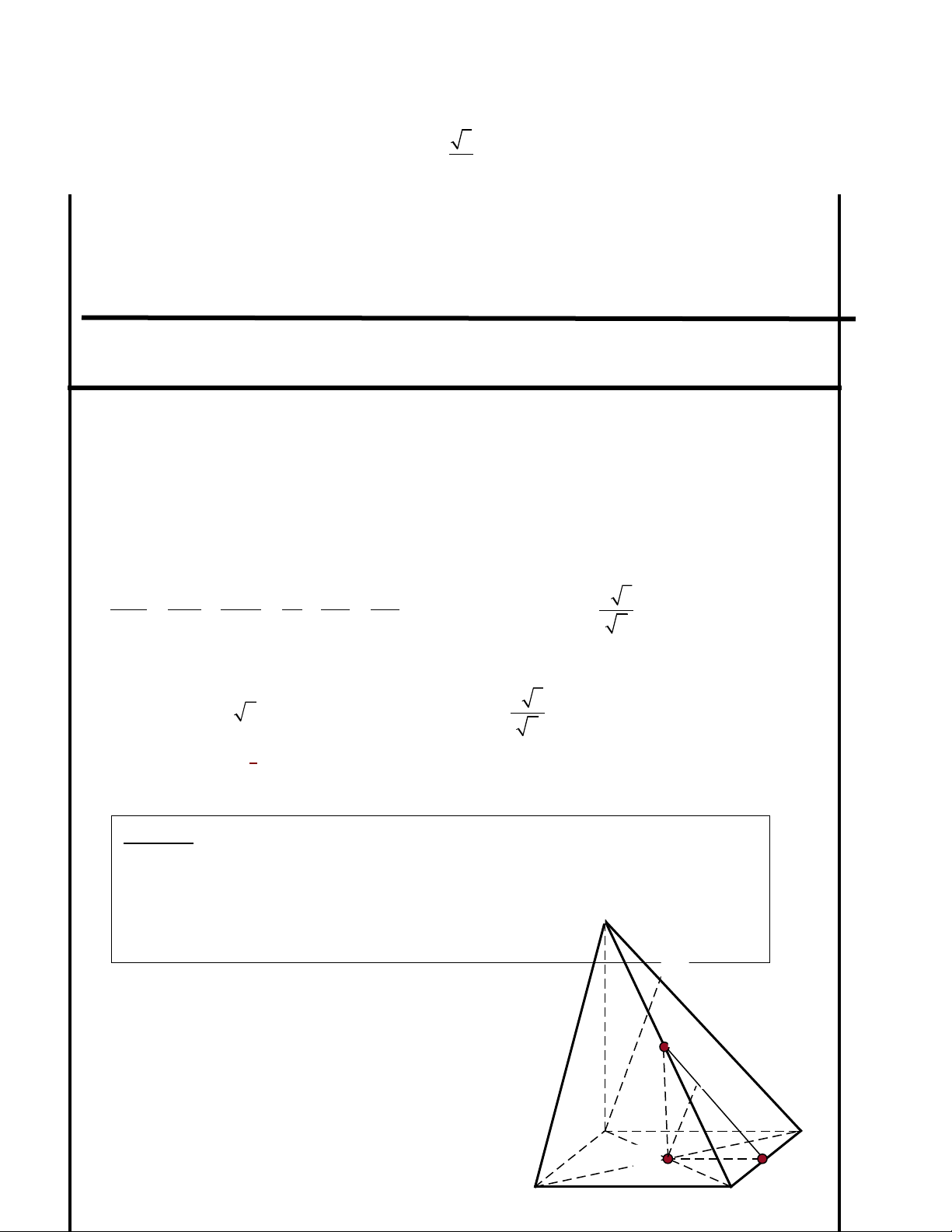
Ví duï 3: Cho h×nh chãp S.ABCD cã ®¸y ABCD lµ h×nh vu«ng c¹nh a,
SA (ABCD), SA = h. Gäi O lµ t©m h×nh vu«ng ABCD. TÝnh kho¶ng
c¸ch:
1) Tõ B ®Õn (SCD) 2) Tõ O ®Õn (SCD)
3)Gi a SC và BD 4) Gi a AB và SC ữ ữ
S
B
A
D
C
O
K
I
H
E