PH NG PHÁP TÍNH TOÁN V TRÍ ƯƠ Ị TÀU THEO MA TR N VÒNG Đ NG CAOẬ Ẳ
THIÊN TH TRONG HÀNG H I THIÊN VĂNỂ Ả
POSITION COMPUTING METHOD WITH CIRCLES OF ALTITUDE EQUAL
MATRIX IN CELESTIAL NAVIGATION
KS. NGUY N VĂN S NGỄ ƯỚ
ThS. ĐÀO QUANG DÂN
Khoa Đi u khi n tàu bi n, ề ể ể Tr ng ĐHHHườ
Tóm t tắ : Bài báo đ a ra ph ng pháp m i đ tính toán v trí tàu trên c s thi t l p và gi i cácư ươ ớ ể ị ơ ở ế ậ ả
ma tr n vòng đ ng cao thiên th . V i ph ng pháp này, v trí tàu s có đ chính xác cao h nậ ẳ ể ớ ươ ị ẽ ộ ơ
nhi u so v i ph ng pháp đ ng cao v trí c a Saint – Hilaire. ề ớ ươ ườ ị ủ
Abstract : This paper introduces the new method computing vessel position with establishing and
solving circles of altitude equal matrix. The astronomical vessel position in this method have higher
accuracy than intercept method of Saint – Hilaire.
1. Đ t v n đ :ặ ấ ề
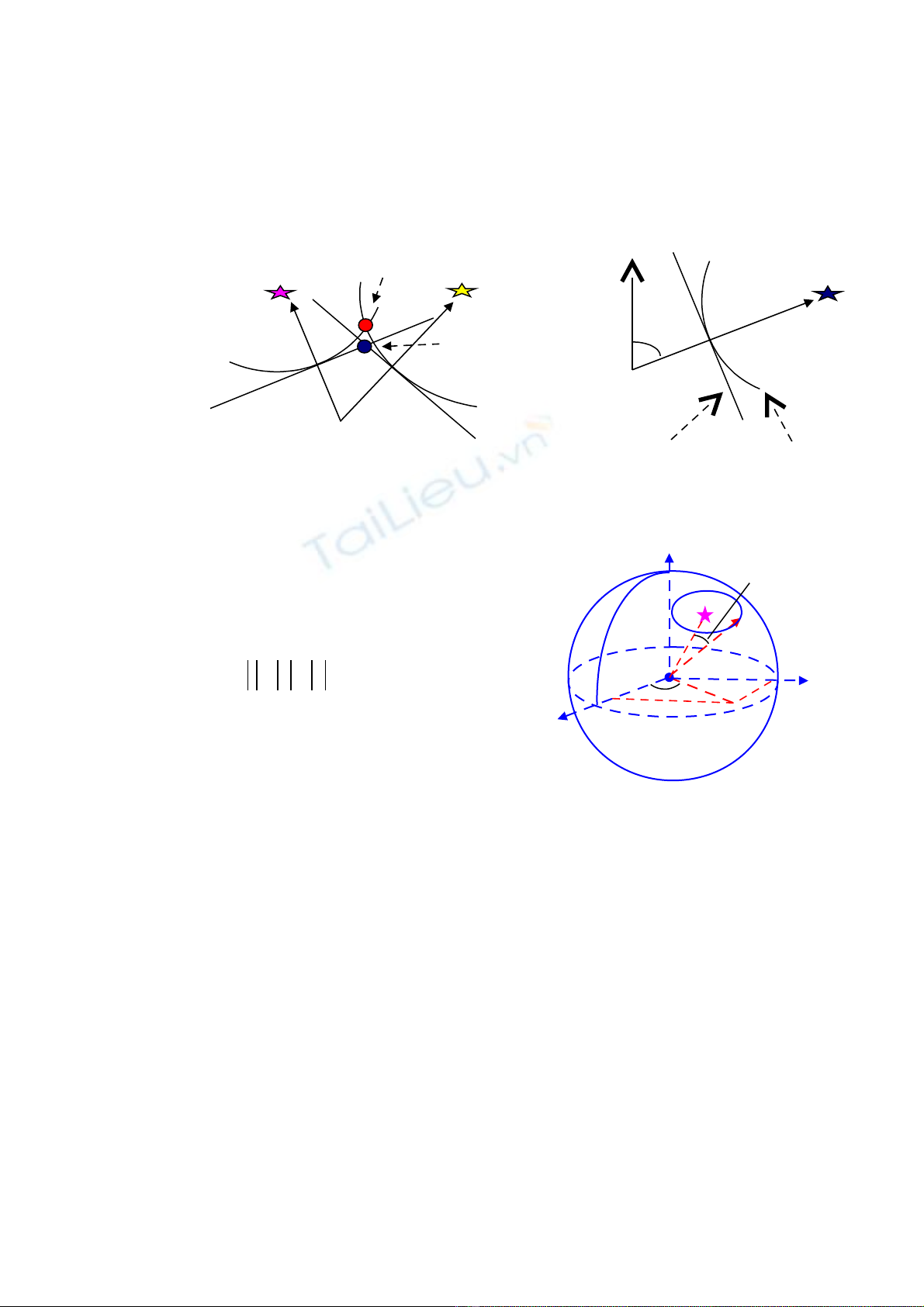
Trong Hàng h i thiên văn, v trí tàu là giao đi m c a ít nh t 2 vòng đ ng cao (ả ị ể ủ ấ ẳ hình 1). Tuy
nhiên, do không v đ c chính xác vòng đ ng cao trên h i đ , h n n a vi c gi i các ph ng trìnhẽ ượ ẳ ả ồ ơ ữ ệ ả ươ
vòng đ ng cao ẳ d ng l ng giác c u khá ph c t p nên th c ti n hàng h i s d ng m t đ ngở ạ ượ ầ ứ ạ ự ễ ả ử ụ ộ ườ
ti p tuy n v i vòng đ ng cao g n v trí d đoán đ thay th , đ ng này đ c g i là đ ng caoế ế ớ ẳ ở ầ ị ự ể ế ườ ượ ọ ườ
v trí. Giao đi m c a các đ ng cao v trí s cho v trí tàu. Ph ng pháp này do nhà hàng h iị ể ủ ườ ị ẽ ị ươ ả
Saint – Hilaire đ xu t, đã đ c các nhà khoa h c ti p t c phát tri n và đ c s d ng đ n ngàyề ấ ượ ọ ế ụ ể ượ ử ụ ế
nay (hình 2).
Th c t , s thay th trên đã m c sai s ph ng pháp trong vi c xác đ nh v trí tàu, ngoài raự ế ự ế ắ ố ươ ệ ị ị
nó còn m c các sai s khi thi t l p đ ng cao v trí. Đ lo i tr các sai s , đ ng th i nâng cao đắ ố ế ậ ườ ị ể ạ ừ ố ồ ờ ộ
chính xác v trí tàu xác đ nh b ng thiên th , trong bài báo này nhóm tác gi đ a ra ph ng phápị ị ằ ể ả ư ươ
tính toán v trí tàu trên c s thi t l p và gi i tr c ti p các ph ng trình vòng đ ng cao thiên th ị ơ ở ế ậ ả ự ế ươ ẳ ể ở
d ng gi i tích. ạ ả
Ph ng trình vòng đ ng cao có d ng :ươ ẳ ạ
sinh sin .sin cos .cos .cos
s L
t
ϕ δ ϕ δ
= +
(1)
Trong đó:
hs - đ cao th t c a thiên th sau khi đã hi u ch nh; ộ ậ ủ ể ệ ỉ
φ – vĩ đ ng i quan sát; δ – xích vĩ c a thiên th ;ộ ườ ủ ể
tL - góc gi đ a ph ng c a thiên th ờ ị ươ ủ ể
N u quan sát đ cao c a 2 thiên th Cế ộ ủ ể 1 và C2 có đ cao l n l t hộ ầ ượ S1, hS2 s nh n đ c hẽ ậ ượ ệ
2 ph ng trình v i 2 n s là ươ ớ ẩ ố φ, tL. Vi c gi i h r t ph c t p, sai s trong các phép toán gây sai sệ ả ệ ấ ứ ạ ố ố
l n đ n v trí tàu, th c ti n s d ng ph ng pháp đ ng cao v trí nh sau: đ cao thiên th đ cớ ế ị ự ễ ử ụ ươ ườ ị ư ộ ể ượ
bi u di n theo hàm s hể ễ ố S = h(φ0; λ0), khai tri n hàm s này theo chu i Taylor t i v trí Mể ố ỗ ạ ị C(φC;λC)
B quaỏ thành ph n ầvô
cùng bé b cậ cao f( Δφ, Δλ)
và đ t ặΔh=h(φ0, λ0) – h(φc, λc),
đ ng th iồ ờ tính các đ o hàm riêng c a đ cao ạ ủ ộ h theo giá tr φ, λ t i Mị ạ C nh n đ c đ ng cao v tríậ ượ ườ ị
[1].
cos sin
sin .
.
.
cc
h A A
λ
ϕ ϕ
∆ = ∆ + ∆
Đây chính là đ ng ti p tuy n v i vòng đ ng cao thiên th g n Mườ ế ế ớ ẳ ể ầ C, thành ph n b c caoầ ậ
f( Δφ, Δλ) là sai s c a ph ng pháp đ ng cao v trí Saint – Hilaire. Ngoài ra khi đ gi i đ ngố ủ ươ ườ ị ồ ả ườ
cao v trí trên h i đ còn mang nh ng sai s khi v ị ả ồ ữ ố ẽ AC, Δh. Nh ng nguyên nhân trên gây ra sai sữ ố
không nh đ i v i v trí tàu xác đ nh. ỏ ố ớ ị ị
0
0
( )
( ; ) ( ; ) . . ( , )
( )
c
c
c
c
dh dh
h h f
dd
ϕ ϕ ϕ λ ϕ λ
λ λ ϕλ
= + ∆ + ∆ + ∆ ∆
2. Thi t l p ph ng trình vòng đ ng cao thiên th b ng ma tr n vector và ph ng phápế ậ ươ ẳ ể ằ ậ ươ
tính toán v trí tàu theo ma tr n vòng đ ng cao:ị ậ ẳ
Trong hàng h i thiên văn, ảvòng đ ng cao thiên th đ c bi u di n d i d ng ph ng trìnhẳ ể ượ ể ễ ướ ạ ươ
(1). Nhóm tác gi xây d ng vòng đ ng cao b ng ma tr n vector:ả ự ẳ ằ ậ
Xét h t a đ vuông góc ệ ọ ộ (OXYZ), thiên c u có bán kính R b t kỳ (ch n R=1), thiên th ầ ấ ọ ể C
(hình 3) có t a đ nhọ ộ ư sau:
Trong đó:
Thiên đ nh ỉZ (X; Y;Z) có t a đ :ọ ộ
Suy ra:
Ph ng trình vòng đ ng cao :ươ ẳ
N u thay t a đ c u c aế ọ ộ ầ ủ thiên th và thiênể
đ nh ng i quan sát vào ph ng trình gi i tích s thu đ c ph ng trình vòng cao d ng (1) : ỉ ườ ươ ả ẽ ượ ươ ạ
M tặ khác,
gi s thiên th ả ử ể Ci b t kỳ có t a đấ ọ ộ (xi; yi; zi) trên thiên c u, v trí ng i quan sát ầ ị ườ Z(X; Y; Z) là giao
đi m c a các vòng đ ng caoể ủ ẳ
os . ost
:os . int
G
G
x c c
y c s
C
z sin
δ
δ
δ
=
=
=
. . .OC x i y j z k
= + +
uuur r r r
. . .i j j k k i 0
i j k 1
= = =
= = =
rr r r rr
r r r
. ....: ; :
x X
OC y OZ Y
z Z
�� � �
�� � �
�� � �
�� � �
�� � �
uuur
uuuv
os . os
: os .
X c c
Z Y c sin
Z sin
ϕ λ
ϕ λ
ϕ
=
=
=
h
i
ii
y
.X + .Y + .Z = sin
x z
Si
0
. . . os(90 )
S
S
OC OZ R R c h sinh
−
= =
uuur uuur
cos . os . os . os os . . os . .
cos . os .( os . os . ) .
cos . os . os .
G G Si
G G Si
LSi
t
t
t t
t
c c c c sin c sin sin sin sinh
c c c sin sin sin sin sinh
c c sin sin sinh
δ ϕ λ δ ϕ λ δ ϕ
δ ϕ λ λ δ ϕ
δ ϕ δ ϕ
+ + =
+ + =
+ =
Δh
vòng đ ng caoẳ
đ ng cao v tríườ ị
MC
AC
NT
Hình 2. Đ ng cao v trí trên h i đườ ị ả ồ
v trí xác đ nh ị ị
MC
v trí th tị ậ
Hình 1. V trí th t và v trí xác đ nh b ng ị ậ ị ị ằ
ph ng pháp đ ng cao v tríươ ườ ị
O
x
y
C
900-hS
Z
δ
z
Hình 3. Thiên c u trên h t a đ vuông gócầ ệ ọ ộ
Tr ng h p ườ ợ quan sát đ cao 2 thiên thộ ể, ma tr n vòng đ ng cao thu đ c:ậ ẳ ượ
Gi i ma tr n trên tìm đ c 2 nghi m k t h p v i v trí d đoán cho v trí chính xác Mả ậ ượ ệ ế ợ ớ ị ự ị 0(X, Y, Z)
Tr ng h p t ng quát, ườ ợ ổ quan sát n >2 thiên th thu đ c ma tr n sau: ể ượ ậ
Ph ng pháp gươ i i tr c ti p :ả ự ế
Trong đó :
A : ma tr n t a đ vuông góc c a thiên thậ ọ ộ ủ ể
X : ma tr n t a đ vuông góc c a thiên đ nh ng i quan sátậ ọ ộ ủ ỉ ườ
B : ma tr n đ cao thiên thậ ộ ể
At : ma tr n chuy n v c a Aậ ể ị ủ
(At.A)-1 : ma tr n ngh ch đ o c a (Aậ ị ả ủ t.A)
Theo ph ng pháp tr c ti p s tính toán đ c nghi m c a ma tr n vòng đ ng cao. Tuy nhiên,ươ ự ế ẽ ượ ệ ủ ậ ẳ
trong th c t đ cao thiên th luôn ch u tác đ ng c a sai s , d n đ n các vòng đ ng cao sự ế ộ ể ị ộ ủ ố ẫ ế ẳ ẽ
không giao c t t i m t đi m mà s c t nhau t ng đôi m t. Đ tính toán v trí t i u nh t s d ngắ ạ ộ ể ẽ ắ ừ ộ ể ị ố ư ấ ử ụ
ph ng pháp gi i gián ti p.ươ ả ế
Ph ng pháp gi i gián ti p ươ ả ế :
Khi có sai s tác đ ng đ n đ cao thiên th ố ộ ế ộ ể hS ph ng trình vòng đ ng cao có d ngươ ẳ ạ
Nghi m t i u c a bài toán th a mãn đi u ki n t ng bình ph ng sai s nh nh t : ệ ố ư ủ ỏ ề ệ ổ ươ ố ỏ ấ
S đ t giá tr nh nh t khi : [2]ạ ị ỏ ấ
=>
1
1 1
1
2
2 2
2
.
... ... ... ...
n
n n
n
y
x sinh
zX
y
x sinh
zY
Z
y
x sinhz
� � � �
��
� � � �
��
� � � �
=
��
� � � �
��
� � � �
�� � �
� � � �
� �
1
1 1
1
22 2
2.
1
X
y
x sinh
z
Y
y
x sinh
z
X Y Z Z
� �� � � �
� �� � � �
=
� �� � � �
� �� � � �
� �� � � �
2
2
1 1
.........
n n
s
i
i
ii
i
i i
S ( . .Y .Z sinh ) min
y
x X z
ε
= =
= = + + −
� �
2.
1 1 1 1
2.
1 1 1 1
2.
1 1 1 1
. .
. .
. .
Si
Si
Si
n n n n
i
i i i
i i
i i i i
n n n n
ii i
i i i
i i i i
n n n n
i i i
iii
i i i i
y
x x x x
z
y y y y
x z
y
xz z z z
sinh
X
Ysinh
Zsinh
= = = =
= = = =
= = = =
� � � �
� � � �
� � � �
� � � �
� � � �
��
� � � �
��
=
� � � �
��
� � � �
��
��
� � � �
� � � �
s
i
ii
i
i
. .Y .Z sinh
y
x X z
ε
+ + = +
0
0
0
S
X
S
Y
S
Z
=
=
=
1
1
1
.( . ) 0
. .
.( . . . ) 0
.( . . . ) 0
n
i i i
iSi
i
n
i
i
i i Si
i
n
i i
iiSi
i
y
x x z
y y
x z
y
x
z z
XY Z sinh
X Y Z sinh
X Y Z sinh
=
=
=
+ + − =
+ + − =
+ + − =
1 1
1
t t
t t t t
tt
A.X B
.A .X .B
A A
( ) ( )
.A . .A .X .A . .B
A A A A
()
A
X
.
.B
A
.
A . .
− −
−
=
=
=
=
=>
Gi i ma tr nả ậ và chuy n đ i t a đ vuông góc (X; Y;Z) sang h t a đ đ a d nh sau: ể ổ ọ ộ ệ ọ ộ ị ư ư
=>
( e2
là đ l ch tâm c a mô hình ellipxoid trái đ t theo h tr c đ a WGS – 84ộ ệ ủ ấ ệ ắ ị )
3. K t lu n:ế ậ
Ngày nay v i ti n b c a khoa h c k thu t, đ c bi t là s phát tri n v t b c c a côngớ ế ộ ủ ọ ỹ ậ ặ ệ ự ể ượ ậ ủ
ngh thông tin đã cho phép gi i nh ng bài toán có kh i l ng l n các phép tính siêu ph c t pệ ả ữ ố ượ ớ ứ ạ
trong th i gian ng n. Sau nhi u năm nghiên c u, nhóm tác gi đã xây d ng nên m t ph ng phápờ ắ ề ứ ả ự ộ ươ
m i – xác đ nh v trí tàu b ng ph ng pháp ma tr n vòng đ ng cao trong hàng h i thiên văn.ớ ị ị ằ ươ ậ ẳ ả
Ph ng pháp mà nhóm tác gi đã trình bày trên không nh ng ch c ch n cho v trí tàu xác đ nhươ ả ở ữ ắ ắ ị ị
chính xác h n ph ng pháp đ ng cao v trí c a Saint – Hilaire mà còn đ c ng d ng vào cácơ ươ ườ ị ủ ượ ứ ụ
ch ng trình cũng nh ph n m m tin h c giúp ng i sĩ quan hàng h i thao tác xác đ nh v trí tàuươ ư ầ ề ọ ườ ả ị ị
m t cách nhanh chóng và hi u qu nh t. ộ ệ ả ấ
Tài li u tham kh o:ệ ả
[1]. Ths, TTr. Nguy n C nh S n. “ễ ả ơ Thiên văn hàng h i 1,2,3”. ảĐ i h c Hàng h i 2004ạ ọ ả
[2]. PGS, TS. Lê Đ c Toàn. “ trích y u ứ ế Ph ng pháp bình ph ng nh nh t”ươ ươ ỏ ấ
Ng i ph n bi n:ườ ả ệ PGS, TS Nguy n C nh S n Tr ng Đ i h c Hàng h i Vi t Nam ễ ả ơ ườ ạ ọ ả ệ
2 2 2
2 2
)
( ).(1
Z
Zarctg
tgu X Y e
X Y
YY
tg arctg
XX
ϕ
λλ
=
=
+ −� �
+=>
� �
� �
==
� �
2 2 2
ar ( ).(1 )
ar
Z
XY
Y
X
D
eD D
D
D
ctg
ctg
ϕ
λ
=
+ −
=
2 2 2
22
2 2 2 2
2
22 2
. . .
.
..
.........
.......
. . .( . ) .( . ) .( . )
2( . )( . )( . )
( . ( . ) ) ( . . . . .
..
)
( .
i i
i i
i i
ii i
i i i
i i
i i
i i
i i i
i i i i i
i ii i i i
i
X
i i
i i i i
yy y y
xzx x x
z z z
y y
x x z z
y y y y
x sinh sinh x x
D z z z z z
y
y y
sinh xz z
D
� � � � � � � � �
� � �
� � � � � � � � �
� � �
= − − − +
= − − − +
2
2
2 2 2
.. .
.
2
. .
2
2 2
2
.. . .
. )
( . ( . ) )
.......
( . . . . . )
( . . )
( . ( . ) ) ( . . . . . )
..
i
ii
i i i ii i i i i
i i i
i i
i
Y
i i
i i i i i
i i
i i i i
i i i i
i
i
i i i i i
Z
y
x z
y y
sinh x x sinh x x xD z z z z z
y
y y
x sinh x x
z z z
y y y y y
sinh x sinh x
D z z z z z
x
� �
� � � � � � � � �
� � � � �
� � � � � � � �
−
= − − − +
−
= − − − +
2
.
.
.........
.............
( . . )
, ,
i i
i i i ii i i
X Y Z
y y y
sinh x x x
z z
D D D
X Y Z
D D D
� � � � �
−
= = =