PHƯƠNG TRÌNH , HỆ PHƯƠNG TRÌNH MŨ VÀ LÔGARIT
(Chương trình nâng cao)
I. Mục tiêu:
+ Về kiến thức:
- Nắm vững các phương pháp giải phương trình mũ và lôgarit.
- Nắm được cách giải hệ phương trình mũ và lôgarit.
+ Về kỹ năng:
- Biết vận dụng tính chất các hàm số mũ, hàm số lôgarit và hàm số luỹ
thừa để giải toán .
- Củng cố và nâng cao kỹ năng của học sinh về giải các phương trình .
hệ phương trình mũ và lôgarit.
+ Về tư duy và thái độ:
- Rèn luyện tư duy logic
- Cẩn thận , chính xác.
- Biết qui lạ về quen
II. Chuẩn bị của giáo viên và học sinh:
+ Giáo viên: Giáo án , phiếu học tập
+ Học sinh: SGK, chuận bị bài tập, dụng cụ học tập.
III. Phương pháp: Gợi mở, giải quyết vấn đề, thảo luận nhóm.
IV. Tiến trình bài học:
1. Ổn định tổ chức: (2')
2. Kiểm tra bài cũ: (5')
- Nêu cách giải phương trình mũ và lôgarit cơ bản .
- Nêu các phương pháp giải phương trình mũ và lôgarit
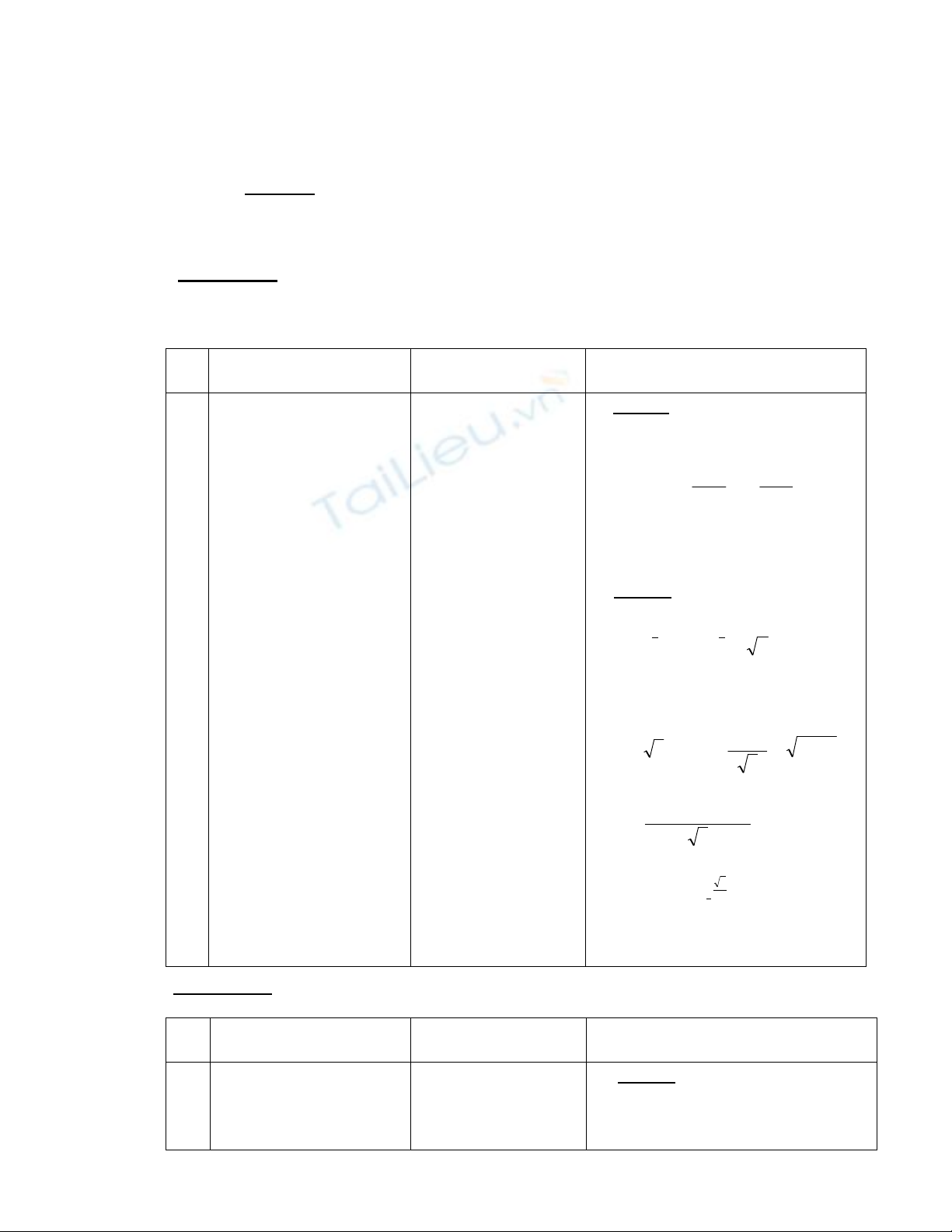
- Bài tập : Giải phương trình
31log)3(log 22 xx
HS Trả lời . GV: Đánh giá và cho điểm
3. Bài mới:LUYỆN TẬP
Tiết thứ 1 :
Hoạt động 1: Phiếu học tập 1
Tg Hoạt động của GV Hoạt động của HS Ghi bảng
(1')
(7')
(2')
- Chia 2 nhóm
- Phát phiếu học tập 1
- Đề nghị đại diện 2
nhóm giải
- Cho HS nhận xét
- Nhận xét , đánh giá
và cho điểm
0
log xxa x
a
- Thảo luận nhóm
- Đại diện của 2
nhóm lên bảng trình
bày
- Nhận xét
a. BT 74c:
1log1log1loglog 7.135.357 xxxx
xlog
75.5
5
5
.3
7
7
.13 log
loglog x
xx
KQ : S =
100
b. BT 75d :
x
xx 2
1
log
2
1
log 44 33 (1)
Đk : x > 0
(1)
3.x
x
x4
4
4log
log
log 4
3
3
3
x
xx
4
44 log
loglog 2
3
33.3
KQ : S =
4
3
log
2
3
4
Hoạt động 2: Phiếu học tập 2
Tg Hoạt động của GV Hoạt động của HS Ghi bảng
(1')
(2’)
- Phát phiếu học tập 2
- Hỏi:Dùng công thức
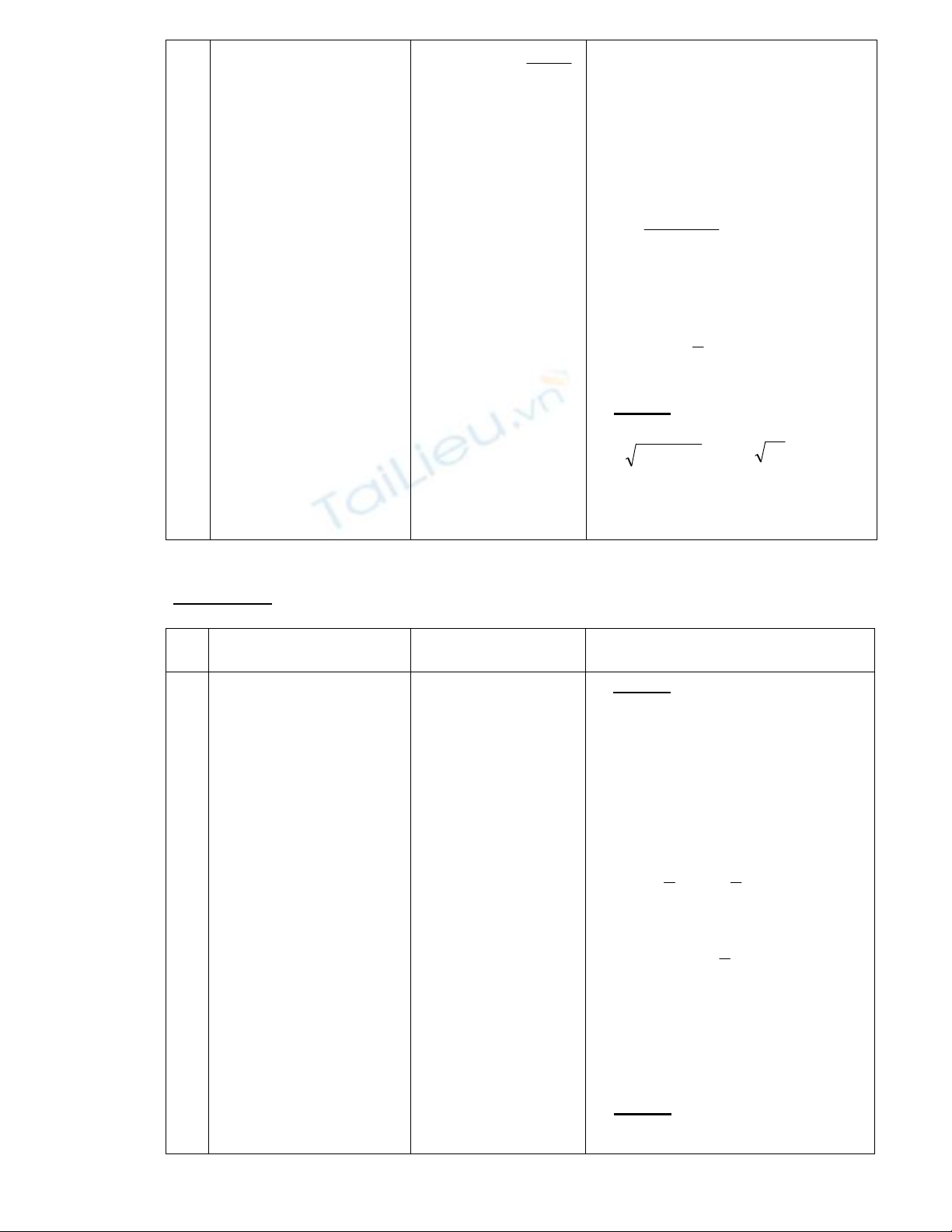
- Thảo luận nhóm a . BT 75b :
log x – 1 4 = 1 + log2(x – 1) (2)
(7')
(2')
nào để đưa 2 lôgarit về
cùng cơ số ?
- Nêu điều kiện của
từng phương trình ?
- Chọn 1 HS nhận xét
- GV đánh giá và cho
điểm
- TL: a
b
b
alog
1
log
- 2 HS lên bảng giải
- HS nhận xét
Đk : 0 < x – 1
1
2
1
x
x
(2)
1log12log2 21 x
x
1log1
1log
22
2
x
x
Đặt t = log2(x – 1) , t 0
KQ : S =
4
5
,3
b. BT 75c :
5
2
22 loglog xx
KQ : S =
25
2;1
Hoạt động 3: Phiếu học tập 3
Tg Hoạt động của GV Hoạt động của HS Ghi bảng
15’
- Phát phiếu học tập 3
- Đề nghị đại diện 2
nhóm giải
- Gọi 1 hs nêu cách giải
phương trình
Nhận xét : Cách giải
phương trình dạng
A.a2lnx
+B(ab)lnx+C.b2lnx=0
Chia 2 vế cho b2lnx
hoặc a2lnx hoặc ablnx để
- Thảo luận nhóm
- Đại diện của 2
nhóm lên bảng trình
bày
- Trả lời
- Nhận xét
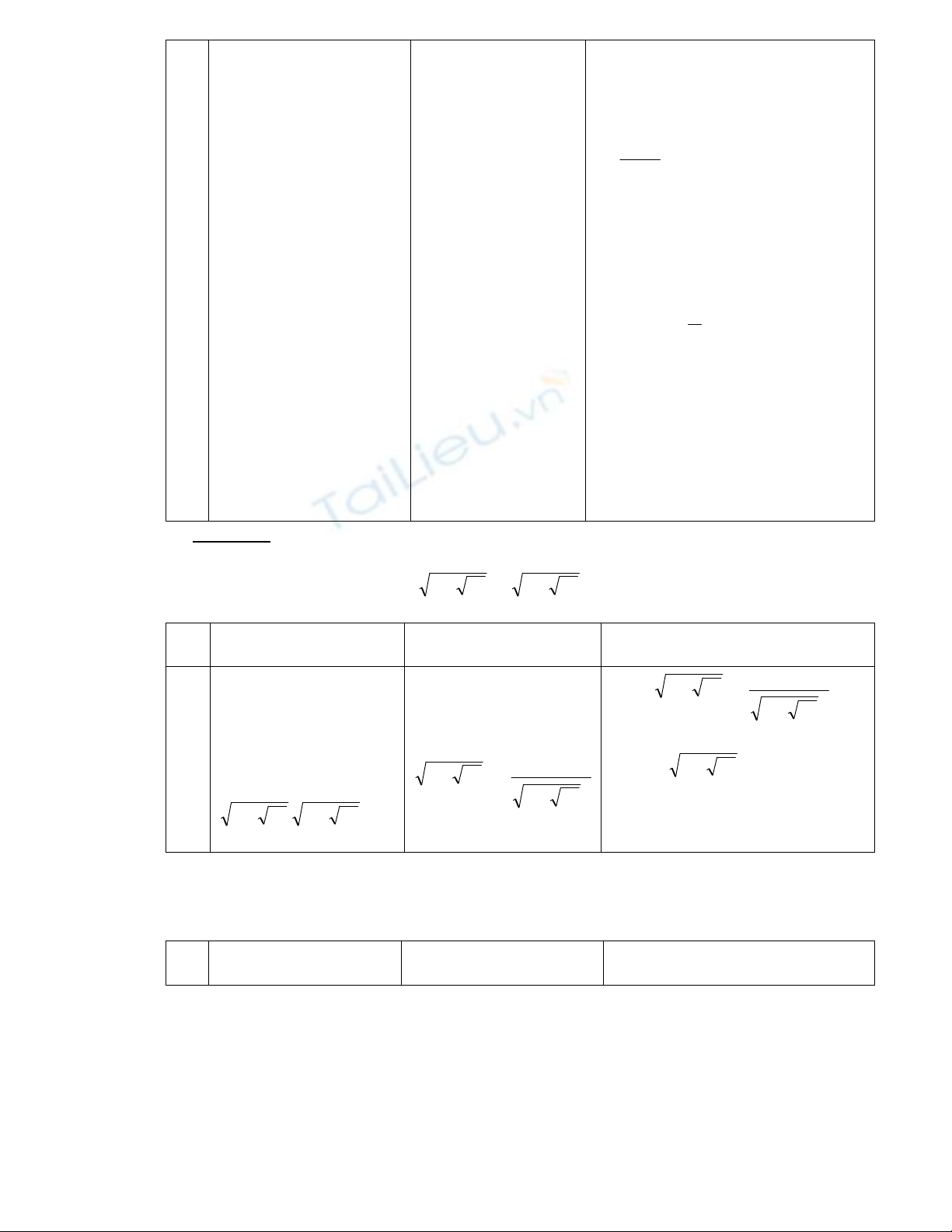
a. BT 76b :
03.264 2lnln1ln 2 xxx
Đk : x > 0
pt 03.1864.4 ln.2lnln xxx
018
3
2
3
2
.4
lnln2
xx
Đặt t = 0,
3
2ln
t
x
KQ : S = 2
e
b. BT 77a :
đưa về phương trình
quen thuộc .
- Gọi học sinh nhận xét
- Hỏi : có thể đưa ra
điều kiện t như thế nào
để chặt chẽ hơn ?
- Nhận xét , đánh giá
và cho điểm
- TL : Dựa vào tính
chất 1cos0 2 x
221 2
cos x
21
t
62.42 22 cossin xx
062.42 22 coscos1 xx
062.4
2
22
2
cos
cos x
x
Đặt t = 0,2 2
cos t
x
KQ : Phương trình có một họ
nghiệm x = Zkk ,
2
4. Củng cố :
BT : Giải phương trình : 12356356 xx
Tg Hoạt động của GV Hoạt động của HS Ghi bảng
(3’)
- Gọi hs nêu cách giải
phương trình dựa vào
nhận xét
1356.356
- TL : Biến đổi
x
x
356
1
356
pt 12
356
1
356
x
x
Đặt t = 0,356 t
x
Tiết thứ 2 :
Hoạt động 1 : Phiếu học tập số 4
Tg Hoạt động của GV Hoạt động của HS Ghi bảng
15’
- Phát phiếu học tập 4
- Đề nghị đại diện 2
nhóm giải
- Goị hs nhận xét
- GV nhận xét , đánh
giá và cho điểm .
- Thảo luận nhóm
- Đại diện của 2 nhóm
lên bảng trình bày
- Nhận xét
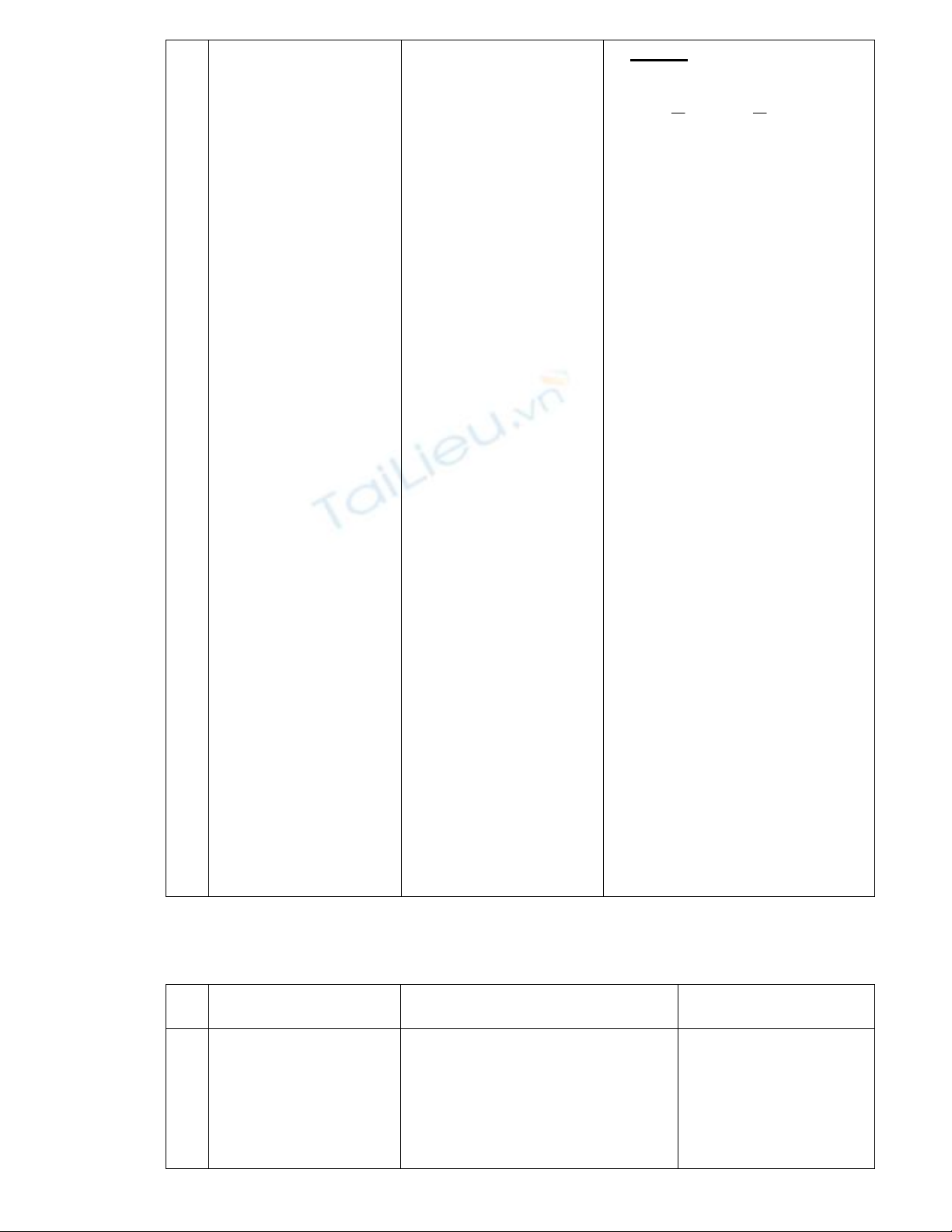
a. BT 78b :
1
5
cos
5
sin
xx
- thay x = 2 vào pt được x = 2 là
một nghiệm .
- Xét x > 2 không có giá trị nào
của x là nghiệm của pt .
- Xét x < 2 không có giá trị nào
của x là nghiệm của pt.
KQ : S =
2
b. log2x + log5(2x + 1) = 2
Đk:
012
0
x
x 0
x
- thay x = 2 vào pt được x = 2 là
một nghiệm .
- Xét x > 2 không có giá trị nào
của x là nghiệm của pt .
- Xét x < 2 không có giá trị nào
của x là nghiệm của pt.
KQ : S =
2
Hoạt động 2 : Phiếu học tập số 5
Tg Hoạt động của GV Hoạt động của HS Ghi bảng
- Phát phiếu học tập 5
- Giải bài toán bằng
phương pháp nào ?
- Thảo luận nhóm
- TL : Phương pháp lôgarit hoá
- TL : a .Cơ số 5
a. x4.53 = 5log
5x
Đk : 10
x
pt
5log5.log 34
5x
x