47
§8. Ruùt goïn bieåu thöùc chöùa caên thöùc baäc hai
Muoán ruùt goïn moät bieåu thöùc, ta caàn phaûi vaän duïng toång hôïp
caùc pheùp tính vaø caùc pheùp bieán ñoåi ñaõ bieát moät caùch linh hoaït .
Ví duï 1 : Ruùt goïn 5
4
4
65 +−+ a
a
a
a vôùi a > 0.
Giaûi
5
4
2
6
55
4
4
65 2+−+=+−+ a
a
aaa
a
a
a
a
565235 +=+−+= aaaa
Ví duï 2 : Chöùng minh ñaúng thöùc
(1 2 3)(1 3 2 ) 2 2++ −+ =
Giaûi
Ta bieán ñoåi veá traùi coù :
22 )3()21()321)(321( −+=−+++
2232221 =−++=
Veá traùi baèng veá phaûi. Vaäy ñaúng thöùc ñuùng.
48
Baøi taäp
58. Ruùt goïn bieåu thöùc :
a.
21
42
918
−+ b.
16 1 4
236
32775
+−
c.
20 45 3 18 72−+ + d.
14,5 12,5
2++
Giaûi
a.
214 1112
42 22 2
9183 3 2
32 2
⎛⎞
−+ = −+ = + =
⎜⎟
⎝⎠
b.
12
81
16 1 4 8 1 12 33
5
236
32775
3353 3 53
+−
+−=+−= =
c.
20 45 3 18 72−+ +
25 35 92 62 152 5=−++= −
d.
11355513592
4,5 12,5
22
21010 2
++
++ =++= =
59. Ruùt goïn caùc bieåu thöùc :
a. 32
5325236 29aa aba−+ −(a,b>0)
b. 333 3
64 3 12 2 9 5 81ab a b ab ab b a b−+− ( vôùi a>0, b>0)
Giaûi
a. 32
5325236 29aa aba−+ −
()
515 12 6
12 15 1
aaaba a
ab a
=− + −
=−−
b.
()
333 3
64 3 12 2 9 5 81
863 6 45
863 39
ab a b ab ab b a b
bab abab abab abab
ab b ab ab
−+−
=− + −
=−−
60. Giaûi phöông trình:
a) 4459.
3
1
5204 =−−−+− xxx
b) 11644991616 +−=+++−+ xxxx
Giaûi
49
a. 1
420 5 .9454
3
xx x−+−− −=
25 5 54
52 54 9
xxx
xxx
⇔−+−−−=
⇔−=⇔−=⇔=
b.
16 16 9 9 4 4 16 1
x
xx x+− ++ +=− +
413121 116
14 116 15
xxxx
xx x
⇔+−+++++=
⇔+=⇔+=⇔=
61. Chöùng minh ñaúng thöùc
3233231
) . 6 2. 4. . 6 2. 4.
2322326
a⎛⎞⎛⎞
+− +− =
⎜⎟⎜⎟
⎜⎟⎜⎟
⎝⎠⎝⎠
3
1
26:6
3
2
x
6
x. ) =
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛++ xx
x
b vôùi x > 0
Giaûi
a.VT
323323
. 6 2. 4. . 6 2. 4.
232232
⎛⎞⎛⎞
=+− +−
⎜⎟⎜⎟
⎜⎟⎜⎟
⎝⎠⎝⎠
22
36661
.6 2. 4.
23266
VP
⎛⎞⎛⎞
=+− = ==
⎜⎟⎜⎟
⎜⎟⎜⎟
⎝⎠⎝⎠
b. VT 62
x. 6 : 6
x3
x
x
x
⎛⎞
=++
⎜⎟
⎜⎟
⎝⎠
71
6:6 2
32
x
xVP
⎛⎞
===
⎜⎟
⎝⎠
50
Luyeän taäp
62. Ruùt goïn :
a.
11
48 2 75 54 5 1
23
−−+
b.
(
)
2
65 120+−
Giaûi
a.
11
48 2 75 54 5 1
23
−−+
10 10
23 103 36 83 36
33
24 9 2 10 14 9 2
33
=− −+=−−+
−+ + −+
==
b.
(
)
2
65 120+−= 6 +2 30 +5 - 120 =11
63. Ruùt goïn :
a.
aab
ab
bba
++ vôùi a > 0, b > 0
b.
2
2
48 4
81
12
m m mx mx
xx
−+
+
−+ vôùi m>0 vaø x ≠1
Giaûi
a. 11 2aab
ab a b a b
bbabb b
⎛⎞⎛⎞
++ = ++ = +
⎜⎟⎜⎟
⎝⎠⎝⎠
b. 2
2
48 4
81
12
m m mx mx
xx
−+
+
−+
()
(
)
()
()
2
92 21
41
19 91
11 4 2
91
mmxx
mx
m
xx
mmxm
x
+
−+
−
=+ =
−−
−+
=−
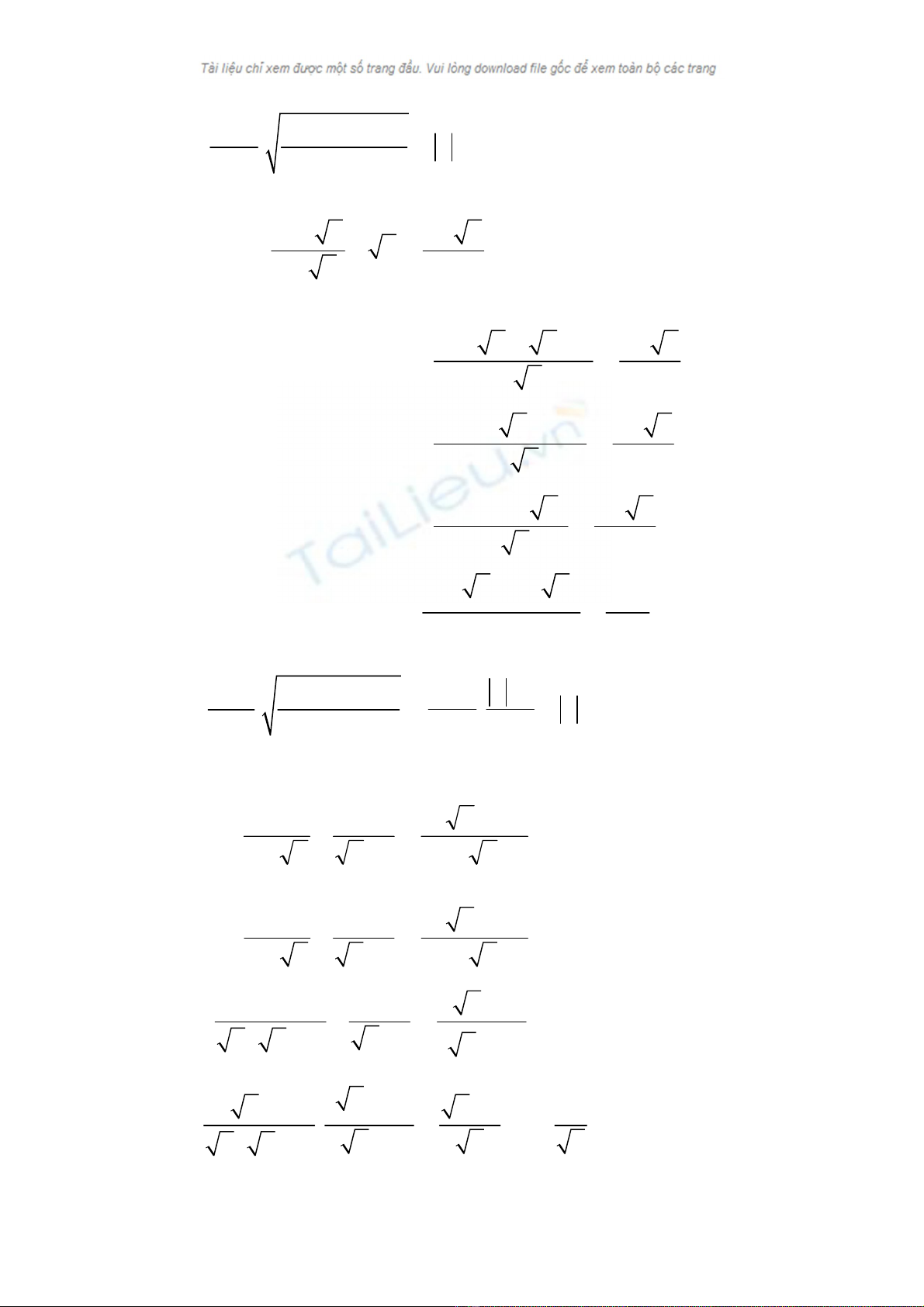
64. Chöùng minh caùc ñaúng thöùc:
a) 1
1
1
1
12
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+
−
−
a
a
a
a
aa vôùi a > 0 vaø a ≠ 1
51
b)
24
22 2
.2
ab ab a
baabb
+
=
++ vôùi a + b > 0 vaø b ≠ 0
Giaûi
a.
2
11
1
1
aa a
VT a a
a
⎛⎞⎛⎞
−−
=+
⎜⎟⎜⎟
⎜⎟⎜⎟
−
−
⎝⎠⎝⎠
=
()()
2
2
2
11
1
1
1(1)1
1
1
(1 )(1 ) 1
1
1
11 11
11
aa a a a
a
a
aaa a
a
a
aa a
a
a
aaaVP
aa
⎛⎞⎛⎞
−+− −
=⎜⎟⎜⎟
⎜⎟⎜⎟
−
−
⎝⎠⎝⎠
⎛⎞⎛⎞
−+ − −
=⎜⎟⎜⎟
⎜⎟⎜⎟
−
−
⎝⎠⎝⎠
⎛⎞⎛⎞
−+ −
=⎜⎟⎜⎟
⎜⎟⎜⎟
−
−
⎝⎠⎝⎠
−+ −
====
−
b.
24
22 2
.2
+
++
ab ab
baabb
2
2.ab
ab aVP
ab
b
+
===
+
65. Ruùt goïn roài so saùnh giaù trò cuûa M vôùi 1, bieát:
12
1
:
1
11
−−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
−
=aa
a
aaa
M vôùi a > 0 vaø a ≠ 1.
Giaûi
11 1
:
121
a
Maa a a a
⎛⎞
+
=+
⎜⎟
−−−−
⎝⎠
() ()
()
()
2
2
11 1
:
1
11
1
111
.1
1
1
a
a
aa a
a
aa
aaa
aa
⎛⎞
+
⎜⎟
=+
⎜⎟
−
−−
⎝⎠
−
+−
===−
+
−