1
S GIÁO D C VÀ ĐÀO T O THANH HOÁỞ Ụ Ạ
TR NG THPT NÔNG C NG IƯỜ Ố
SÁNG KI N KINH NGHI MẾ Ệ
PHÁT TRI N T DUY HÀM CHO H C SINH Ể Ư Ọ
QUA CÁC BÀI TOÁN V PH NG TRÌNH VÔ TỀ ƯƠ Ỉ
Ng i th c hi n: Tr n Thanh Minhườ ự ệ ầ
Ch c v : Giáo viênứ ụ
SKKN thu c môn: Toánộ
M C L CỤ Ụ
N i dungộTrang
I. M ĐUỞ Ầ
1. Lí do ch n đ tài.ọ ề
2. M c đích c a đ tài.ụ ủ ề
3. Đi t ng, ph m vi. ố ượ ạ
4. Ph ng pháp nghiên c u.ươ ứ
II. N I DUNG SÁNG KI N KINH NGHI M.Ộ Ế Ệ
1. Các m nh đ và tính ch t th ng dùng.ệ ề ấ ườ
3
2. Các d ng toán c th .ạ ụ ể
D ng 1ạ. Các bài toán s d ng hàm s đi di n.ử ụ ố ạ ệ 4
D ng 2:ạ Các bài toán áp d ng tr c ti p đo hàmụ ự ế ạ 8
BÀI T P T NG TẬ ƯƠ Ự 12
3. Hi u qu c a sáng ki nệ ả ủ ế
III. K T LU N.Ế Ậ 13
2
TÊN Đ TÀI:Ề
PHÁT TRI N T DUY HÀM CHO H C SINH QUA CÁCỂ Ư Ọ
BÀI TOÁN V PH NG TRÌNH VÔ TỀ ƯƠ Ỉ
I. M ĐU.Ở Ầ
1. Lý do ch n đ tài.ọ ề
Nh chúng ta đã bi t, chuyên đ v ph ng trình chi m m t l ng kháư ế ề ề ươ ế ộ ượ
l n trong ch ng trình toán h c ph thông. Tuy nhiên, trong s các bài t p đóớ ươ ọ ổ ố ậ
có m t l ng l n các bài t p mà ta không th gi i đc b ng ph ng phápộ ượ ớ ậ ể ả ượ ằ ươ
thông th ng, ho c có th gi i đc nh ng g p r t nhi u khó khăn và ph cườ ặ ể ả ượ ư ặ ấ ề ứ
t p.ạ
Nh ng ta đã bi t gi a ph ng trình và hàm s có m i liên h ch t chư ế ữ ươ ố ố ệ ặ ẻ
v i nhau, khi đnh nghĩa ph ng trình ng i ta đã d a trên khái ni m hàm s ,ớ ị ươ ườ ự ệ ố
nên n u chúng ta bi t s d ng ki n th c v hàm s đ gi i các bài toán vế ế ử ụ ế ứ ề ố ể ả ề
ph ng trình thì chúng ta đc nh ng l i gi i nhanh g n và đn gi n h n r tươ ượ ữ ờ ả ọ ơ ả ơ ấ
nhi u. Tuy nhiên, không ph i bài toán nào cũng có th s d ng hàm s đề ả ể ử ụ ố ể
gi i, nh ng nh ng ng d ng đo hàm c a hàm s đ gi i ph ng trình, hả ư ữ ứ ụ ạ ủ ố ể ả ươ ệ
ph ng trình…, là r t l n. Chính vì v y tôi ch n đ tài ươ ấ ớ ậ ọ ề “ Phát tri n t duyể ư
hàm cho h c sinh qua các bài toán v ph ng trìnhọ ề ươ vô t ”ỉ nh m giúp cácằ
em h c sinh có thêm m t ph ng pháp n a khi khi gi i các bài toán vọ ộ ươ ữ ả ề
ph ng trình vô t .ươ ỉ
2. M c đích yêu c u.ụ ầ
- Trang b cho h c sinh thêm m t ph ng pháp gi i ph ng trình vô tị ọ ộ ươ ả ươ ỉ
mang l i hi u qu cao.ạ ệ ả
- B i d ng cho h c sinh v ph ng pháp, k năng gi i toán. Qua đóồ ưỡ ọ ề ươ ỹ ả
h c sinh nâng cao kh năng t duy, sáng t o khi gi i toán.ọ ả ư ạ ả
3. Đi t ng nghiên c u.ố ượ ứ
- Các d ng toán v ph ng trình vô t trong ch ng trình toán h c phạ ề ươ ỉ ươ ọ ổ
thông.
- Phân lo i các d ng toán th ng g p và ph ng pháp gi i.ạ ạ ườ ặ ươ ả
4. Ph ng pháp nghiên c u.ươ ứ
Ph ng pháp chung c a d ng bài t p này: S d ng các tính ch t vươ ủ ạ ậ ử ụ ấ ề
tính đn đi u c a hàm s đ gi i.ơ ệ ủ ố ể ả
II. N I DUNG SÁNG KI N KINH NGHI M.Ộ Ế Ệ
1. Các m nh đ và tính ch t th ng dùng.ệ ề ấ ườ
3
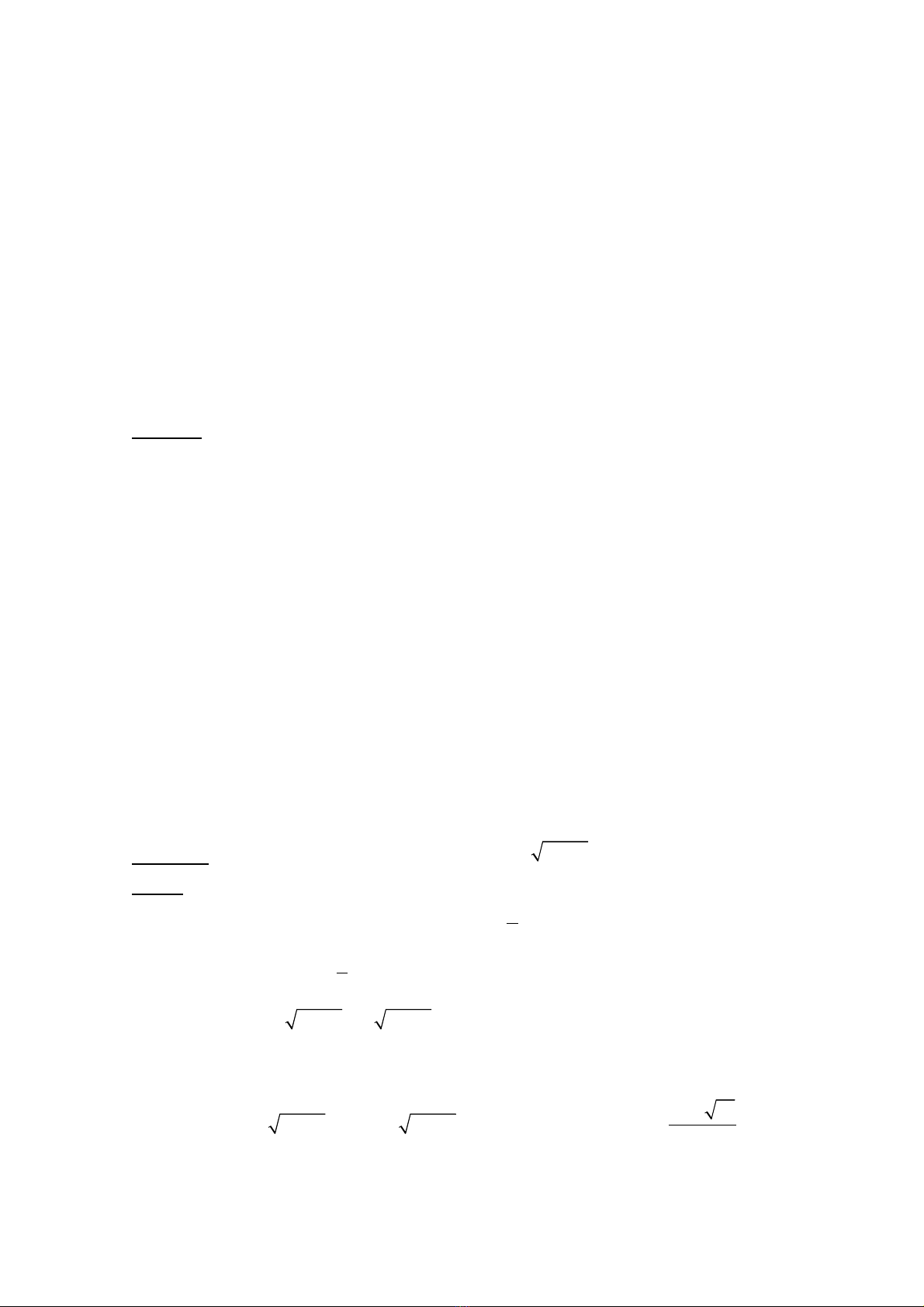
a) Cho hàm số
( )y f x=
xác đnh trên kho ng ị ả
( )
;a b
. N u hàm sế ố
( )y f x=
đn đi u trên kho ng ơ ệ ả
( )
;a b
thì ph ng trình ươ
( ) 0f x =
, n u cóế
nghi m trên kho ng ệ ả
( )
;a b
thì nghi m đó là duy nh t.ệ ấ
b) Cho hàm s ố
( )y f x=
đn đi u trên kho ng ơ ệ ả
( )
;a b
,
( )
1 2
; ; .x x a b∀
Ta có
1 2
( ) ( )f x f x=
1 2.x x=�
c) Cho ph ng trình ươ
( ) ( )f x g x=
xác đnh trên kho ng ị ả
( )
;a b
. N u m tế ộ
trong hai hàm s ố
( )f x
ho c ặ
là hàm đn đi u trên kho ng ơ ệ ả
( )
;a b
, hàm còn
l i là hàm h ng s ho c đn đi u ng c l i v i hàm kia trên kho ng ạ ằ ố ặ ơ ệ ượ ạ ớ ả
( )
;a b
,
thì ph ng trình n u có nghi m thì nghi m đó là duy nh t.ươ ế ệ ệ ấ
2. Các d ng toán c th .ạ ụ ể
D ng 1ạ. Các bài toán s d ng hàm s đi di n.ử ụ ố ạ ệ
Ph ng trình đã cho có th bi n đi đc v d ng ươ ể ế ổ ượ ề ạ
( ) ( )f u f v=
trong
đó
( )u u x=
,
( )v v x=
.
B c 1:ướ Bi n đi ph ng trình v d ngế ổ ươ ề ạ
( ) ( )f u f v=
.
B c 2:ướ Xét hàm s ố
( )y f t=
trên
D
(v i ớ
t
là bi n đi di n cho ế ạ ệ
,u v
.
D
ch aứ
t p giá tr c a hàm s ậ ị ủ ố
( ); ( )u u x v v x= =
) .
- Tính
'y
. Xét d u ấ
'y
.
- K t lu n tính đn đi u c a hàm s ế ậ ơ ệ ủ ố
( )y f x=
trên
D
.
B c 3:ướ K t lu n.ế ậ
- Ph ng trình đã cho có nghi m khi và ch khi ươ ệ ỉ
u v=
, gi i ph ng trình ả ươ
u v=
.
- K t lu n nghi m c a ph ng trình đã cho.ế ậ ệ ủ ươ
Các ví d c th :ụ ụ ể
Ví d 1.ụ Gi i ph ng trình:ả ươ
( )
2
(4 1) 3 5 2 0x x x x+ + − − =
(1)
Gi i:ả
Đi u ki n xác đnh c a ph ng trình ề ệ ị ủ ươ
5
2
x
T p xác đnh: ậ ị
5
;2
D� �
= −

� �
(1)
( )
3
3
(2 ) 2 5 2 5 2x x x x+ = − + −�
(2)
Xét hàm s ố
3
( )f t t t= +
,
t R
;
2
'( ) 3 1 0; .f t t t R= + > ∀
V y hàm s đng bi n trên ậ ố ồ ế
R
.
(2)
(2 ) ( 5 2 ) 2 5 2f x f x x x= − = −� �
2
01 21
4
4 2 5 0
xx
x x
− +
=� �
+ − =
4
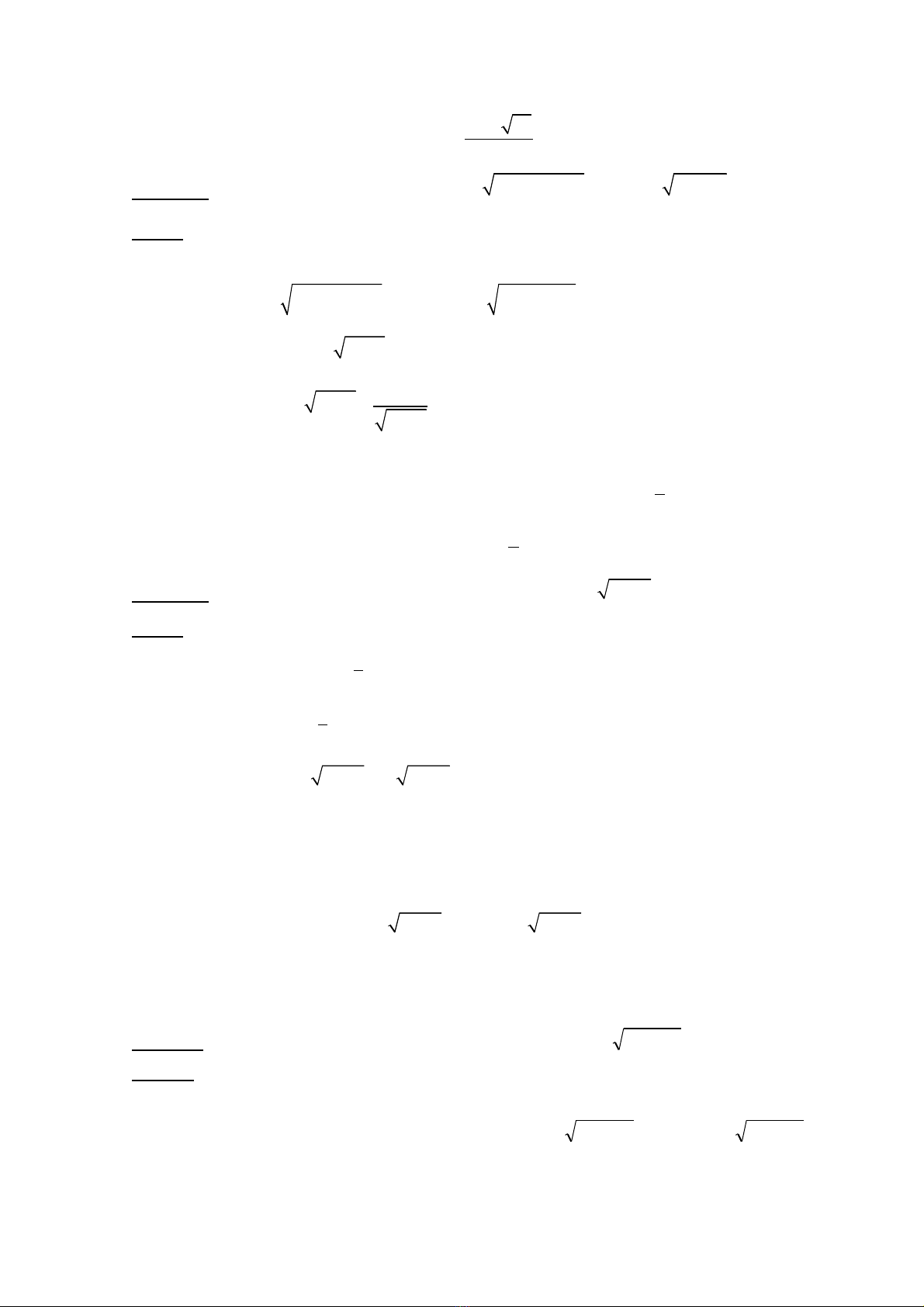
V y nghi m c a ph ng trình là ậ ệ ủ ươ
1 21
4
x− +
=
Ví d 2.ụ Gi i ph ng trình:ả ươ
( )
()()
2 2
2 1 . 2 4 4 4 3 2 9 3 0x x x x x+ + + + + + + =
(1)
Gi i:ả
T p xác đnh: ậ ị
D R=
(1)
( ) ( )
( )
( ) ( )
( )
2 2
2 1 . 2 2 1 3 3 2 3 3x x x x+ + + + = − + − +�
(2)
Xét hàm s ố
()
2
( ) 2 3f t t t= + +
trên
D R=
Đo hàm ạ
2
2
2
'( ) 2 3 0,
3
t
f t t
t
= + + + >
+
t R
∀
V y hàm s đng bi n trên ậ ố ồ ế
D R=
Ph ng trình (2) ươ
1
(2 1) ( 3 ) 2 1 3 5
f x f x x x x+ = − + = − = −� �
V y nghi m c a ph ng trình (1) là ậ ệ ủ ươ
1
5
x= −
Ví d 3.ụ Gi i ph ng trình: ả ươ
( )
3 2
3 4 2 3 2 3 1x x x x x+ + + = + +
(1)
Gi i:ả
Đi u ki n xác đnh ề ệ ị
1
3
x −
T p xác đnh: ậ ị
1;
3
D� �
= − +
� �
(1)
( )
3
3
( 1) 1 3 1 3 1x x x x+ + + = + + +�
(2)
Xét hàm s ố
3
( ) ,f t t t= +
Đo hàm ạ
2
'( ) 3 1 0,f t t t R= + > ∀
V y hàm s đng bi n trên ậ ố ồ ế
R
Đ (2) x y ra thì ể ả
0
( 1) ( 3 1) 1 3 1 1
x
f x f x x x x
=
+ = + + = +� � =
V y nghi m c a ph ng trình là ậ ệ ủ ươ
0
1
x
x
=
=
Ví d 4ụ. Gi i ph ng trình: ả ươ
72427175 2223 xxxxx
Gi iả :
T p xác đnhậ ị :
D R=
Ph ng trình ươ
72727272222 2222
23 xxxxxxx
Xét hàm s ố
3 2
( ) , .f t t t t t R= + +
5