I. M ĐUỞ Ầ
1. Lí do ch n đ tài: ọ ề
Bài toán tìm giá tr nh nh t, giá tr l n nh t c a hàm s nói riêng vàị ỏ ấ ị ớ ấ ủ ố
b t đng th c nói chung là m t trong nh ng ch đ quan tr ng và h p d nấ ẳ ứ ộ ữ ủ ề ọ ấ ẫ
trong ch ng trình gi ng d y và h c b môn toán tr ng ph thông. Trongươ ả ạ ọ ộ ở ườ ổ
các đ thi môn toán c a các kì thi đi h c, cao đng, tôt nghi p và thi h c sinhề ủ ạ ọ ẳ ệ ọ
gi i các c p nh ng năm g n đây các bài toán liên qua đn giá tr l n nh t, giáỏ ấ ữ ầ ế ị ớ ấ
tr nh nh t c a hàm s th ng xuyên có m t và th ng là câu h i khó c aị ỏ ấ ủ ố ườ ặ ườ ỏ ủ
đ thi.ề
Đ tìm giá tr nh nh t, giá tr l n nh t c a hàm s hay c a bi u th cể ị ỏ ấ ị ớ ấ ủ ố ủ ể ứ
có nhi u ph ng pháp nh : S d ng b t đng th c cô si, b t đng th cế ươ ư ử ụ ấ ẳ ứ ấ ẳ ứ
Bunhia; ph ng pháp l ng giác hóa; ph ng pháp mi n giá tr ; ph ng phápươ ượ ươ ề ị ươ
đ th và hình h c; ph ng pháp chi u bi n thiên…. Nh ng tôi th y trongồ ị ọ ươ ề ế ư ấ
nh ng năm g n đây, trong các đ thi vi c s d ng đo hàm đ tìm giá tr l nữ ầ ề ệ ử ụ ạ ể ị ớ
nh t,giá tr nh nh t th ng xuyên đc s d ng, chính vì v y trong quá trìnhấ ị ỏ ấ ườ ượ ử ụ ậ
gi ng d y c a mình tôi mu n hình thành cho h c sinh có t duy và k năng sả ạ ủ ố ọ ư ỹ ử
lí các bài toán này d a vào đo hàm.Nên tôi xin trình bày sáng ki n kinhự ạ ế
nghi m: ệ“Phát tri n t duy và k năng c a h c sinh qua bài toán tìm giáể ư ỹ ủ ọ
tr l n nhât, giá tr nh nh t d a vào đo hàm”ị ớ ị ỏ ấ ự ạ .
2. M c đích nghiên c u:ụ ứ
Khi tìm giá tr l n nh t,giá tr nh nh t c a bi u th c có nhi n n tôi nh n ị ớ ấ ị ỏ ấ ủ ể ứ ề ẩ ậ
th y:ấ
H c sinh s , b qua, không h ng thú.ọ ợ ỏ ứ
Lúng túng, th đng, không bi t x lí t đâu.ụ ộ ế ử ừ
V y v n đ đt ra làậ ấ ề ặ :
C n giúp cho h c sinh h th ng và ghi nh đy đ các ki n th cầ ọ ệ ố ớ ầ ủ ế ứ
liên quan : đo hàm và các b t đng th c cô si, bunhiacôpxkiạ ấ ẳ ứ
Giúp h c sinh hình thành và phát tri n t duy linh ho t, sáng t oọ ể ư ạ ạ
trong các bài toán liên quan.
3. Đi t ng nghiên c u:ố ượ ứ
Đ gi i quy t v n đ đó tôi đ xu t ý t ng sau:ể ả ế ấ ề ề ấ ưở
C n cho h c sinh t h th ng l i ki n th c tr ng tâm sau m i bu iầ ọ ự ệ ố ạ ế ứ ọ ỗ ổ
h c t đó kh c sâu đc ki n th c.ọ ừ ắ ượ ế ứ
T các bài toán c th , d n d t h c sinh t đúc k t ra các kinhừ ụ ể ẫ ắ ọ ự ế
nghi m gi i toán qua đó t tìm ra thu t gi i cho các l p bài toánệ ả ự ậ ả ớ
khác nhau.
Cho h c sinh th y đc m i liên h c a ki n th c đang h c v iọ ấ ượ ố ệ ủ ế ứ ọ ớ
th c ti n cu c s ng.ự ễ ộ ố
4. Ph ng pháp nghiên c u:ươ ứ
Xu t pháp t các bài toán c th , cho h c sinh nhìn rõ v n đ và tìmấ ừ ụ ể ọ ấ ề
ra ph ng pháp gi i c th cho các bài toán có s d ng đo hàm.ươ ả ụ ể ử ụ ạ
1
Đúc k t ra thu t toán c a các l p bài toán khác nhau có s d ng đoế ậ ủ ớ ử ụ ạ
hàm.
Th c nghi m s d ng đo hàm trong các bài toán tìm giá tr l n nh tự ệ ử ụ ạ ị ớ ấ
và nh nh t c a hàm s .ỏ ấ ủ ố
II. N I DUNG SÁNG KI N KINH NGHI M:Ộ Ế Ệ
1. C s c a sáng ki n kinh nghi m:ơ ở ủ ế ệ
1.1. B t đng th c cô siấ ẳ ứ :
Cho hai s không âm,ta cóố :
2
a b ab
+
. D u b ng x y ra khi a = b.ấ ằ ả
T ng quát: Cho n s không âm aổ ố 1, a2, …, an. Ta có:
1 2
1 2
.... ...
nnn
a a a a a a
n
+ + +
.D u b ng x y ra khi aấ ằ ả 1 = a2 = …= an.
1.2. B t đng th c Bunhia_ Côpski: ấ ẳ ứ
Cho hai c p s ( a; b) và ( c ; d ), ta có: ặ ố
( ) ( )
( )
2
2 2 2 2
a b c d ac bd+ + +
D u b ng x y raấ ằ ả :
a b
c d
=
1.3. Khái ni m giá tr l n nh t và giá tr nh nh tệ ị ớ ấ ị ỏ ấ :
Cho hàm s y = f (x) xác đnh trên t p D.ố ị ậ
S M đc g i là giá tr l n nh t c a hàm s y = f(x) trên D n uố ượ ọ ị ớ ấ ủ ố ế :
( )f x M x D ∀
và t n t i xồ ạ 0
0
: ( )D f x M=�
.
Kí hi uệ :
max ( )
D
M f x=
S m đc g i là giá tr nh nh t c a hàm s y = f(x) trên D n uố ượ ọ ị ỏ ấ ủ ố ế :
( )f x m x D ∀
và t n t i xồ ạ 0
.
Kí hi uệ : m =
min ( )
D
f x
2. Th c tr ng c a v n đ tr c khi áp d ng sáng ki n kinh nghi m:ự ạ ủ ấ ề ướ ụ ế ệ
Sau khi h c xong khái ni m đo hàm và ng d ng c a đo hàm đ kh o sátọ ệ ạ ứ ụ ủ ạ ể ả
và v đ th hàm s , trong bu i ôn t p tôi l n l t đt ra các ví d đ h cẽ ồ ị ố ổ ậ ầ ượ ặ ụ ể ọ
sinh t gi i. Sau th i gian t năm đn m i phút th c hi n ki m ch ng trênự ả ờ ừ ế ườ ự ệ ể ứ
47 h c sinh c a l p 12a7năm h c 2016 -2017 ọ ủ ớ ọ
Đc đi m c a l p th c nghi m là:ặ ể ủ ớ ự ệ
S h c sinh c a l p: 47 ố ọ ủ ớ
K t qu h c t p v môn toán năm h c 2015 – 2016 là:ế ả ọ ậ ề ọ
7 h c sinh có h c l c gi iọ ọ ự ỏ
13 h c sinh có h c l c kháọ ọ ự
23 h c sinh có h c l c trung bìnhọ ọ ự
4 h c sinh có h c l c y u.ọ ọ ự ế
2
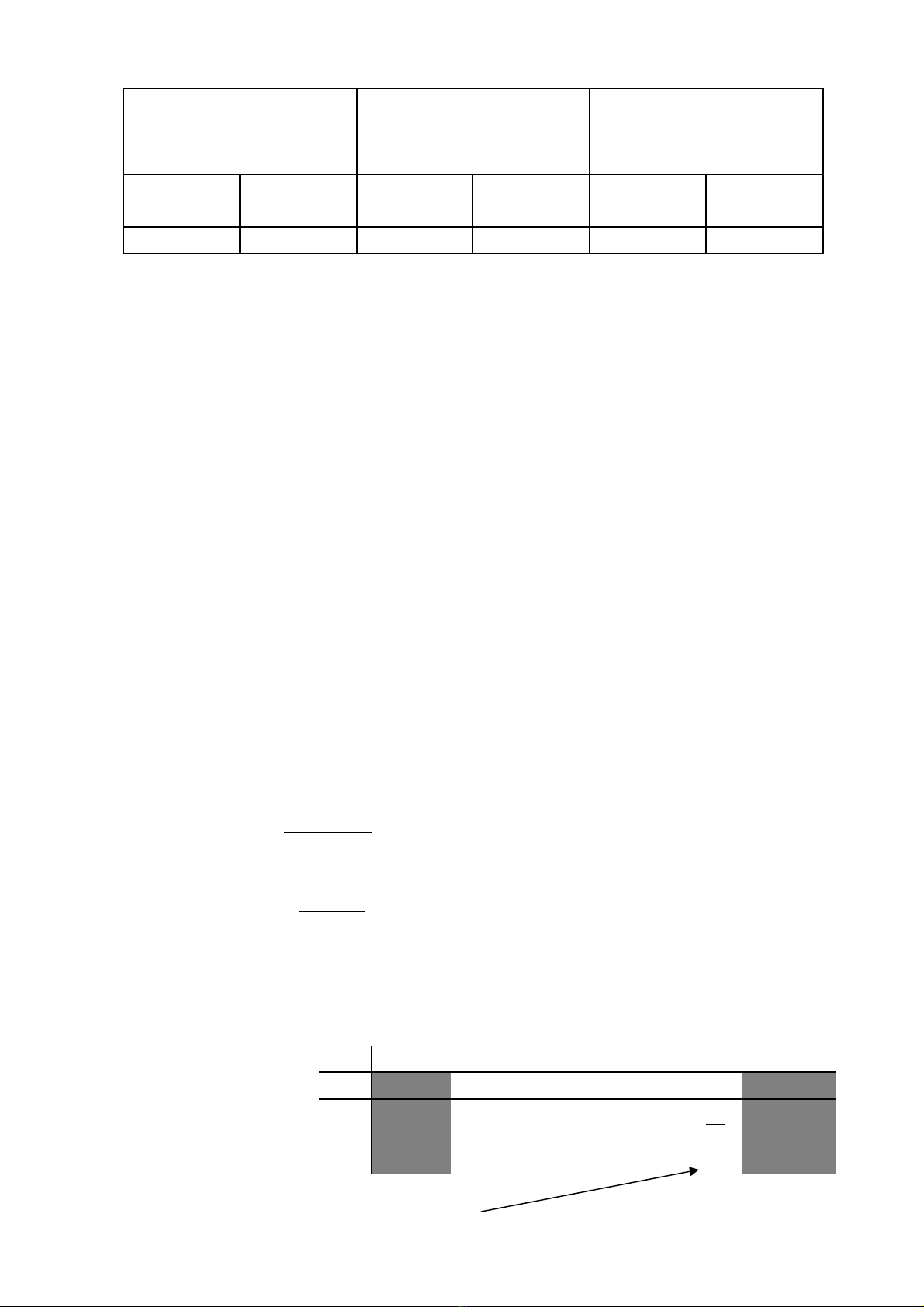
Nh n bi t(n m v ngậ ế ắ ữ
lý thuy t)ếThông hi u(có thể ể
v n d ng lý thuy tậ ụ ế
đ th c hành )ể ự
V n d ng linh ho tậ ụ ạ
trong gi i toánả
S h c ố ọ
sinh
Ph n trămầS h c ố ọ
sinh
Ph n trămầS h c ố ọ
sinh
Ph n trămầ
47 100% 27 57,4% 10 21,3%
3. Các gi i pháp s d ng đ gi i quy t v n đ:ả ử ụ ể ả ế ấ ề
Hình thành t duy và k năng c a h c sinh qua vi c gi i các bài toán tìmư ỹ ủ ọ ệ ả
giá tr l n nh t và giá tr nh nh t:ị ớ ấ ị ổ ấ
Bài toán 1 : Tìm giá tr l n nh t và giá tr nh nh t c a hàm s y = f(x)ị ớ ấ ị ỏ ấ ủ ố
trên D.
Đây là cách s d ng tr c ti p chi u bi n thiên c a hàm s đ tìm giá trử ụ ự ế ề ế ủ ố ể ị
l n nh t và giá tr nh nh t, các bài toán này th ng g p trong các đ thi t tớ ấ ị ỏ ấ ườ ặ ề ố
nghi p, đi h c và cao đng các kh i D, B.ệ ạ ọ ẳ ố
Đ tìm giá tr l n nh t và giá tr nh nh t c a hàm s y = f(x) trên D:ể ị ớ ấ ị ỏ ấ ủ ố
B c 1:ướ L p b ng bi n thiên c a hàm s trên Dậ ả ế ủ ố :
Tính y’ và tìm các đi m t i h nể ớ ạ
Tính gi i h n vô c c và gi i h n t i vô c c (n u có).ớ ạ ự ớ ạ ạ ự ế
B c 2:ướ So sánh giá tr c a hàm s t i các đi m đc bi t ( thôngị ủ ố ạ ể ặ ệ
th ng là các đi m c c đi, c c ti u, các đi m không t n t a đo hàm ....).Tườ ể ự ạ ự ể ể ồ ị ạ ừ
phép so sánh y đ tìm giá tr l n nh t và nh nh t ph i tìm.ấ ể ị ớ ấ ỏ ấ ả
Ví d 1ụ : ( Đi h c kh i D năm 2011 )ạ ọ ố
Tìm giá tr l n nh t và giá tr nh nh t c a hàm sị ớ ấ ị ỏ ấ ủ ố :
2
2 3 3
1
x x
yx
+ +
=+
trên
[ ]
0; 2
Gi i:ả Ta có :
( )
2
2
2 4
'
1
0
' 0 2
x x
y
x
x
yx
+
=+
=
= = −
B ng bi n thiênả ế :
V yậ :
t -
o 2 +
y’ +
Y
17
3
3
3
[ ]
[ ]
0;2
0;2
17
(2) 3
(0) 3
max
min
y
y
y
y
= =
= =
Chú ý : Đi v i bài toán tìm giá tr l n nh t và giá tr nh nh t c a hàmố ớ ị ớ ấ ị ỏ ấ ủ
số
y = f(x) liên t c trên đo n ụ ạ
[ ]
;a b
ta còn có th áp d ng ph ng pháp sauể ụ ươ
đây :
B c 1:ướ Tìm các đi m xế1, x2, ....xn trên
[ ]
;a b
t i đó f’(x) = 0 ho c f’(x) khôngạ ặ
xác đnh.ị
B c 2:ướ Tính f(a), f( x1), f(x2), ….., f(xn).
B c 3:ướ Tìm s l n nh t M và s nh nh t m trong các s trên và k t lu n:ố ớ ấ ố ỏ ấ ố ế ậ
[ ] [ ]
; ;
,
max min
a b a b
M m
y y
= =
Các bài toán trên th c s r t đn gi n, h c sinh không c n hi u b nự ự ấ ơ ả ọ ầ ể ả
ch t c a bài toán v n tìm đc k t qu c a bài toán. Ta có th làm nh sauấ ủ ẫ ượ ế ả ủ ể ư :
Ta có
( )
2
'
2
'
2 4
1
0
02
x x
y
x
x
yx
+
=+
=
= = −
Trong đó nghi m th a mãn trên đo n [0ệ ỏ ạ ; 2] là x= 0
Ta có
( )
0 3y=
và
( )
17
23
y=
V y ậ
[ ]
( )
0;2
min 0 3y y= =
và
[ ]
( )
0;2
17
max y 2 3
y= =
Ví d 2:ụ (Đi h c kh i D năm 2010 )ạ ọ ố
Tìm giá tr nh nh t c a hàm sị ỏ ấ ủ ố :
2 2
4 21 3 10y x x x x= − + + − − + +
trên mi n xác đnh c a nó.ề ị ủ
Ta th y bài toán này khác so v i ví d 1 là bài toán ch a cho ta bi t tìmấ ớ ụ ư ế
giá tr nh nh t c a hàm s trên t p nào, nên b c đu tiên ta ph i ch ra t pị ỏ ấ ủ ố ậ ướ ầ ả ỉ ậ
xác đnh c a hàm s .ị ủ ố
Gi iả
T p xác đnh c a hàm s D= [-2ậ ị ủ ố ;5]
Ta có :
( ) ( )
2 2
2 2
4 2 3 10 3 2 4 21
'
2. 4 21. 3 10
1
' 0 3
x x x x x x
y
x x x x
y x
− − + + − − − + +
=− + + − + +
= =�
B ng bi n thiênả ế :
4
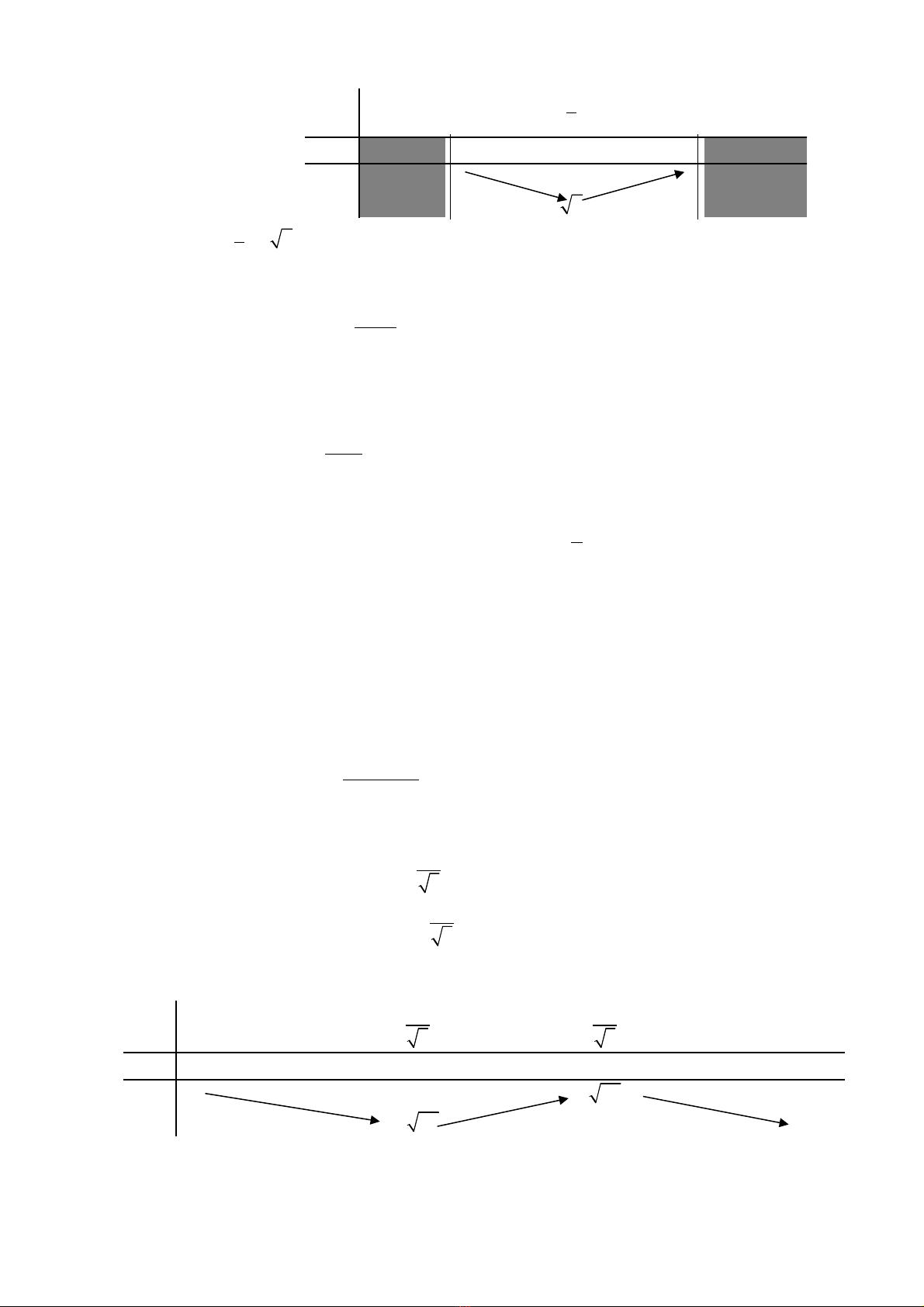
V yậ
[ ]
2;5
1
( ) 2
3
min y
y
−
= =
Ví d 3:ụ Tìm giá tr l n nh t và giá tr nh nh t c a hàm sị ớ ấ ị ỏ ấ ủ ố :
4
4
1
x
yx
=+
Ta th yấ : Trong ví d này khó h n ví d 2, vì t p xác đnh c a hàm sụ ơ ụ ậ ị ủ ố
là t p R, nh v y khi l p b ng bi n thiên h c sinh ph i có ki n th c vè gi iậ ư ậ ậ ả ế ọ ả ế ứ ớ
h n vô c c. Giáo viên nh c l i ki n th c c b n v gi i h n vô c c:ạ ự ắ ạ ế ứ ơ ả ề ớ ạ ự
Cho hàm s ố
( )
( )
f x
yg x
=
v i f(x) và g(x) là các đa th c.ớ ứ
N u b c f(x) > b c g(x)ế ậ ậ :
lim , lim
x x
y y
+ −
k t qu b ng vô c c.ế ả ằ ự
N u b c f(x) = b c g(x)ế ậ ậ :
lim lim
x x
a
y y b
+ −
= =
v i a,b l n l t là h sớ ầ ượ ệ ố
c a x có s mũ cao nh t trong các đa th c f(x) và g(x).ủ ố ấ ứ
N u b c f(x) < b c g(x)ế ậ ậ :
lim lim 0
x x
y y
+ −
= =
Gi iả : T p xác đnh: Rậ ị
Gi i h nớ ạ :
lim lim 0
x x
y y
+ −
= =
Ta có :
( )
( )
4
2
4
4 1 3
'
1
x
y
x
−
=+
4
4
1
3
' 0 1
3
x
y
x
=
= = −
B ng bi n thiênả ế :
x-
-
4
1
3
4
1
3
+
y’ + 0 - 0 +
y0
4
27
-
4
27
0
x-
-2
1
3
5
+
y’ - 0 +
y
2
5