M t s sai l m và ph ng pháp kh c ph c khi gi i bài toán c c tr Đi sộ ố ầ ươ ắ ụ ả ự ị ạ ố
PH N M ĐUẦ Ở Ầ
I. Lý do ch n đ tài:ọ ề
Toán h c là m t môn khoa h c t nhiên, nó ra đi và phát tri n g n li nọ ộ ọ ự ờ ể ắ ề
v i s phát tri n c a xã h i loài ng i. T xa x a con ng i đã bi t đnớ ự ể ủ ộ ườ ừ ư ườ ế ế
Toán h c và khoa h c đã kh ng đnh r ng Toán h c là n n t ng c a nhi uọ ọ ẳ ị ằ ọ ề ả ủ ề
môn khoa h c khác, các ng d ng c a toán h c đa l i hi u qu to l n trongọ ứ ụ ủ ọ ư ạ ệ ả ớ
đi s ng xã h i và là n n t ng t duy tri th c rèn luy n k năng, k x o, phátờ ố ộ ề ả ư ứ ệ ỹ ỷ ả
tri n trí tu , ph m ch t đo đc cho m i con ng i. Do đó vi c d y và h cể ệ ẩ ấ ạ ứ ỗ ườ ệ ạ ọ
b môn Toán không ch d ng l i vi c h c thu c bài toán mà ph i phát huyộ ỉ ừ ạ ở ệ ọ ộ ả
năng l c t duy sáng t o cho h c sinh, trang b cho h c sinh các k năng c nự ư ạ ọ ị ọ ỹ ầ
thi t đ h c sinh có th v n d ng m t cách linh ho t vào th c ti n cu cế ể ọ ể ậ ụ ộ ạ ự ễ ộ
s ng. H n n a vi c đi m i ph ng pháp d y h c tr ng ph thông ph iố ơ ữ ệ ổ ớ ươ ạ ọ ở ườ ổ ả
h ng đn đào t o ngu n nhân l c, b i d ng nhân tài đáp ng yêu c u c aướ ế ạ ồ ự ồ ưỡ ứ ầ ủ
xã h i trong th i k h i nh p qu c t . Nó đòi h i m i ng i giáo viên ph iộ ờ ỳ ộ ậ ố ế ỏ ỗ ườ ả
chú tr ng đn vi c thi t k và h ng d n h c sinh th c hi n các d ng bàiọ ế ệ ế ế ướ ẫ ọ ự ệ ạ
t p phát tri n t duy và rèn luy n k năng, đng viên khuy n khích, t o cậ ể ư ệ ỹ ộ ế ạ ơ
h i và đi u ki n cho h c sinh tham gia m t cách tích c c, ch đng, sáng t oộ ề ệ ọ ộ ự ủ ộ ạ
vào quá trình khám phá và lĩnh h i n i dung bài h c, chú ý khai thác v n ki nộ ộ ọ ố ế
th c, kinh nghi m và kĩ năng đã có c a h c sinh, b i d ng h ng thú, nhuứ ệ ủ ọ ồ ưỡ ứ
c u hành đng và thái đ t tin trong h c t p c a h c sinh, góp ph n phátầ ộ ộ ự ọ ậ ủ ọ ầ
tri n t i đa ti m năng c a b n thân.ể ố ề ủ ả
Toán h c mang tính chính xác r t cao, m t bài toán có th có nhi u cáchọ ấ ộ ể ề
gi i song nó ch có m t đáp s duy nh t. Do đó trong quá trình d y h c toán,ả ỉ ộ ố ấ ạ ọ
giáo viên c n phân tích, tìm tòi và giúp h c sinh phát hi n bài t p đã cho thu cầ ọ ệ ậ ộ
d ng toán nào đ v n d ng ph ng pháp gi i cho phù h p. Trong quá trìnhạ ể ậ ụ ươ ả ợ
gi i toán, h c sinh th ng m c ph i nh ng sai l m mà chính h c sinh cũngả ọ ườ ắ ả ữ ầ ọ
không phát hi n đc nên v n c nghĩ r ng cách gi i c a mình là đúng.ệ ượ ẫ ứ ằ ả ủ
Trong nhi u năm tham gia b i d ng đi tuy n h c sinh gi i môn Toán, b nề ồ ưỡ ộ ể ọ ỏ ả
thân tôi nh n th y d ng toán tìm giá tr l n nh t, nh nh t (g i là bài toán c cậ ấ ạ ị ớ ấ ỏ ấ ọ ự
tr đi s ) thì h c sinh th ng m c ph i nhi u sai l m. T lý do đó nên tôiị ạ ố ọ ườ ắ ả ề ầ ừ
ch n sáng ki n kinh nghi m ọ ế ệ “M t s sai l m và ph ng pháp kh c ph cộ ố ầ ươ ắ ụ
khi gi i bài toán c c tr đi s ” ả ự ị ạ ố đ nghiên c u nh m tìm ra nh ng sai l mể ứ ằ ữ ầ
c b n, tìm hi u nguyên nhân và h ng kh c ph c, giúp h c sinh t tin h n,ơ ả ể ướ ắ ụ ọ ự ơ
chính xác h n khi gi i d ng toán này.ơ ả ạ
Đi m i ph ng pháp d y h c đã và đang di n ra m t cách m nh mổ ớ ươ ạ ọ ễ ộ ạ ẽ
t t c các tr ng và v i m i m t ng i giáo viên. Đã có nhi u nhà khoaở ấ ả ườ ớ ỗ ộ ườ ề
h c, nhi u nhà qu n lý giáo d c và nhi u giáo viên nghiên c u, đa ra nh ngọ ề ả ụ ề ứ ư ữ
sáng ki n hay trong vi c đi m i ph ng pháp d y h c đ nâng cao hi u quế ệ ổ ớ ươ ạ ọ ể ệ ả
giáo d c. Đi m m i c a đ tài này tôi mu n đ c p đn đó là nghiên c u tìmụ ể ớ ủ ề ố ề ậ ế ứ
ra nh ng sai l m c b n trong vi c trình bày bài gi i c a m t bài toán c c tr ,ữ ầ ơ ả ệ ả ủ ộ ự ị
1
M t s sai l m và ph ng pháp kh c ph c khi gi i bài toán c c tr Đi sộ ố ầ ươ ắ ụ ả ự ị ạ ố
t đó tìm ra nguyên nhân và ph ng pháp kh c ph c c th cho t ng sai l m.ừ ươ ắ ụ ụ ể ừ ầ
Giúp h c sinh n m ch c h n và t s a ch a cho mình trong quá trình gi iọ ắ ắ ơ ự ử ữ ả
toán, nh m gây h ng thú h c t p, t o ra ni m say mê môn h c trong m i m tằ ứ ọ ậ ạ ề ọ ỗ ộ
h c sinh. Đng th i giúp t t c các đi t ng h c sinh n m đc ph ngọ ồ ờ ấ ả ố ượ ọ ắ ượ ươ
pháp h c t p đ n m th t ch c ch n ki n th c môn h c, đc bi t là b iọ ậ ể ắ ậ ắ ắ ế ứ ọ ặ ệ ồ
d ng, đào t o nên nh ng h c sinh gi i th c s , t o ngu n nhân l c t ngưỡ ạ ữ ọ ỏ ự ự ạ ồ ự ươ
lai cho đt n c.ấ ướ
II. Ph m vi áp d ng:ạ ụ
Sáng ki n này đc áp d ng trong vi c d y h c phân môn Đi s c pế ượ ụ ệ ạ ọ ạ ố ấ
THCS, trong vi c ôn luy n cho h c sinh d thi tuy n sinh vào l p 10 THPT.ệ ệ ọ ự ể ớ
Đc bi t áp d ng trong công tác b i d ng h c sinh gi i nh m nâng cao ch tặ ệ ụ ồ ưỡ ọ ỏ ằ ấ
l ng đi tuy n d thi h c sinh gi i môn Toán c p t nh.ượ ộ ể ự ọ ỏ ấ ỉ
PH N N I DUNGẦ Ộ
I. Th c tr ng n i dung c n nghiên c u:ự ạ ộ ầ ứ
Th c t cho th y Toán h c là n n t ng cho m i ngành khoa h c, làự ế ấ ọ ề ả ọ ọ
chi c chìa khoá v n năng đ khai phá và thúc đy s phát tri n cho m i ngànhế ạ ể ẩ ự ể ọ
khoa h c, kinh t , quân s ... trong cu c s ng. ọ ế ự ộ ố Chính vì v y vi c d y và h cậ ệ ạ ọ
b môn toán trong nhà tr ng đóng vai trò vô cùng quan tr ng. D y toánộ ườ ọ ạ
chi m v trí s m t trong các môn h c c a nhà tr ng, đi v i giáo viên, d yế ị ố ộ ọ ủ ườ ố ớ ạ
toán là ni m t hào song đó cũng là th thách vô cùng l n. Đ d y toán và h cề ự ử ớ ể ạ ọ
toán t t thì th y và trò không ng ng rèn luy n và đu t trí và l c vào nghiênố ầ ừ ệ ầ ư ự
c u h c h i. H c và d y toán v i ch ng trình c b n đã r t khó, xong d yứ ọ ỏ ọ ạ ớ ươ ơ ả ấ ạ
và h c toán trong đào t o mũi nh n l i vô cùng gian truân, vi c h c và d yọ ạ ọ ạ ệ ọ ạ
không d ng vi c ng i h c và ng i d y ph i có trí tu nh t đnh mà cừ ở ệ ườ ọ ườ ạ ả ệ ấ ị ả
th y và trò ph i dày công đu t vào nghiên c u các d ng toán, thu t toánầ ả ầ ư ứ ạ ậ
v n d ng h p lý các tính ch t toán h c do các nhà toán h c đã nghiên c u vàoậ ụ ợ ấ ọ ọ ứ
gi i toán, ngoài ra ng i d y và h c toán ph i t rèn luy n và nghiên c u đả ườ ạ ọ ả ự ệ ứ ể
có nh ng công trình toán c a riêng mình cùng góp s c đ đa b môn toánữ ủ ứ ể ư ộ
ngày càng phát tri n.ể
Qua quá trình gi ng d y nhi u năm b n thân tôi th y vi c hình thànhả ạ ề ả ấ ệ
cho h c sinh cách suy nghĩ đ tìm l i gi i cho bài toán ho c m i d ng toánọ ể ờ ả ặ ỗ ạ
nào đó là công vi c r t khó. Đng tr c m t bài toán n u ng i th y ch aệ ấ ứ ướ ộ ế ườ ầ ư
hi u, ch a có h ng gi i thì ta h ng d n h c sinh nh th nào, th t khóể ư ướ ả ướ ẫ ọ ư ế ậ
trong nh ng tình hu ng nh th ng i th y s m t vai trò ch đo trong vi cữ ố ư ế ườ ầ ẽ ấ ủ ạ ệ
d y h c sinh, còn h c sinh đã không gi i đc toán nh ng l i m t ni m tin ạ ọ ọ ả ượ ư ạ ấ ề ở
2
M t s sai l m và ph ng pháp kh c ph c khi gi i bài toán c c tr Đi sộ ố ầ ươ ắ ụ ả ự ị ạ ố
th y và c m th y vi c h c toán là c c hình, là khó vô cùng không th h cầ ả ấ ệ ọ ự ể ọ
đc. ượ
Toán h c là b môn khoa h c c a nhân lo i, m t b môn khoa h c đaọ ộ ọ ủ ạ ộ ộ ọ
d ng v th lo i. Không ph i c d y toán và h c toán là bi t h t, là đã đnạ ề ể ạ ả ứ ạ ọ ế ế ế
đnh cao c a trí tu nhân lo i. Khi tr c ti p b i d ng h c sinh gi i tôi tỉ ủ ệ ạ ự ế ồ ưỡ ọ ỏ ự
th y ki n th c toán c a b n thân còn r t h n ch , nh t là nh ng bài toán vấ ế ứ ủ ả ấ ạ ế ấ ữ ề
c c tr trong đi s . Đây là d ng toán l n, có nhi u cách th c đ gi i th ngự ị ạ ố ạ ớ ề ứ ể ả ườ
hay xu t hi n nhi u trong các đ thi h c sinh gi i các c p, thi vào l p 10ấ ệ ề ề ọ ỏ ấ ớ
THPT. Tuy nhiên, nhi u h c sinh không bi t gi i nh th nào? Có nh ngề ọ ế ả ư ế ữ
ph ng pháp nào? Trong khi các tài li u vi t v v n đ này r t h n ch ho cươ ệ ế ề ấ ề ấ ạ ế ặ
ch a h th ng thành các ph ng pháp nh t đnh, gây nhi u khó khăn trongư ệ ố ươ ấ ị ề
vi c h c t p c a h c sinh, d n đn h c sinh d m c ph i các sai l m. ệ ọ ậ ủ ọ ẫ ế ọ ễ ắ ả ầ Vì
v y vi c nghiên c u các sai l m c a h c sinh khi gi i các bài toán c c tr điậ ệ ứ ầ ủ ọ ả ự ị ạ
s là r t thi t th c, giúp giáo viên n m v ng n i dung và xác đnh đcố ấ ế ự ắ ữ ộ ị ượ
ph ng pháp gi ng d y ph n này đt hi u qu , góp ph n nâng cao ch tươ ả ạ ầ ạ ệ ả ầ ấ
l ng d y và h c, đc bi t là ch t l ng h c sinh gi i và giáo viên gi i cácượ ạ ọ ặ ệ ấ ượ ọ ỏ ỏ ở
tr ng THCS. Tôi đã ti n hành kh o sát v ch t l ng làm bài thi c a các emườ ế ả ề ấ ượ ủ
thu c đi tuy n b i d ng HSG l p 9 c p t nh, k t qu thu đc nh sau:ộ ộ ể ồ ưỡ ớ ấ ỉ ế ả ượ ư
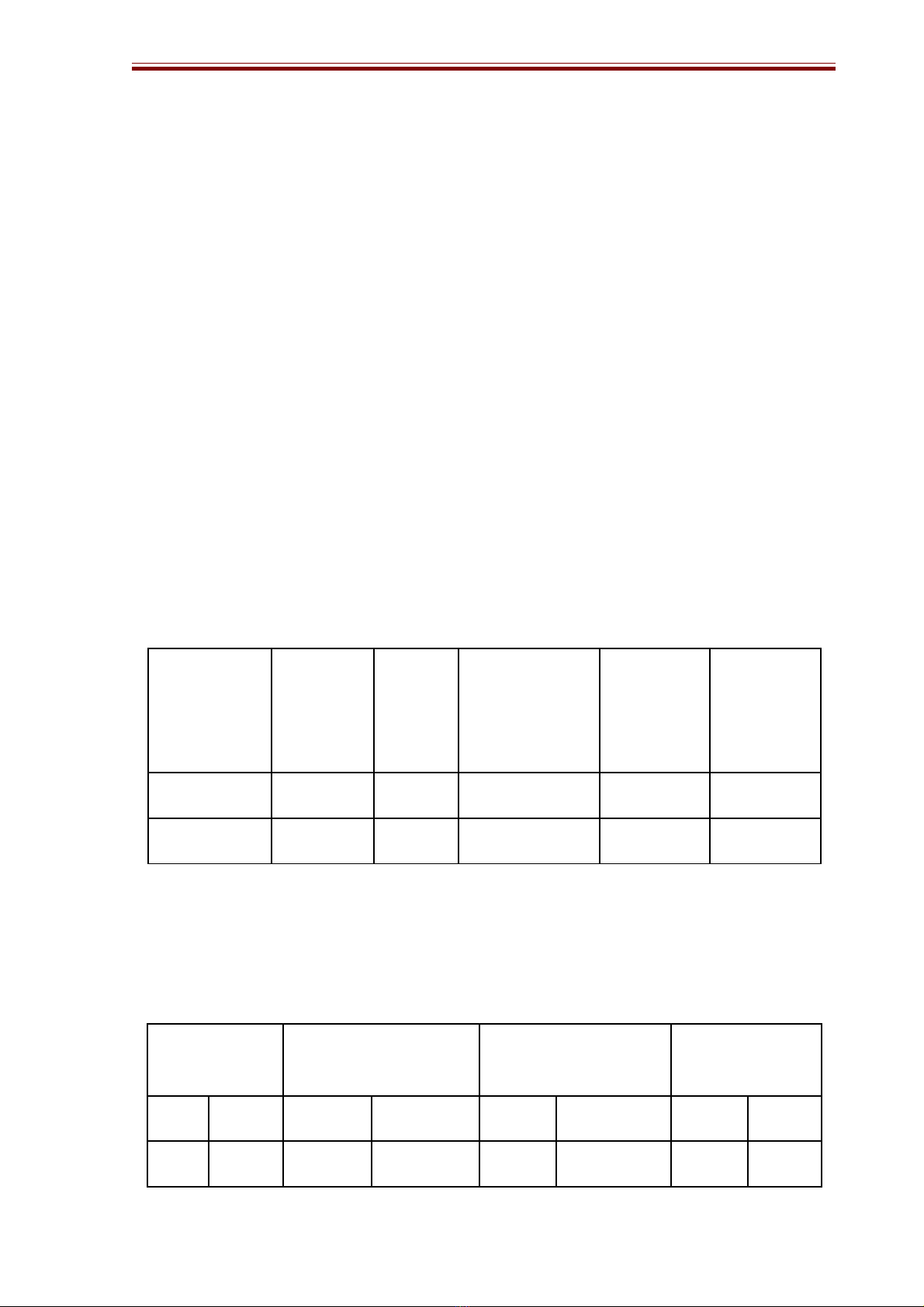
B ng 1: K t qu h c sinh làm bài t p v c c tr đi s trong đ thi HSG c pả ế ả ọ ậ ề ự ị ạ ố ề ấ
t nhỉ
Năm h cọS HSố
tham gia
Ch aư
làm
đcượ
Đã làm
nh ng đnhư ị
h ng cáchướ
gi i saiả
Làm đcượ
nh ngư
ch a xongư
Làm đcượ
c bàiả
2014-2015 20 05 06 05 04
2015-2016 20 06 06 04 03
B c vào đu năm h c tôi ti n hành kh o sát trên 20 h c sinh đangướ ầ ọ ế ả ọ
tham gia b i d ng h c sinh gi i mà tôi đang tr c ti p gi ng d y, v i bàiồ ưỡ ọ ỏ ự ế ả ạ ớ
toán có ki n th c trên m c đ đ tuy n sinh nh ng ch a đn m c đ đ thiế ứ ứ ộ ề ể ư ư ế ứ ộ ề
h c sinh gi i c p t nh, thang đi m 1,5. K t qu thu đc nh sau:ọ ỏ ấ ỉ ể ế ả ượ ư
B ng 2: K t qu kh o sát 20 h c sinh đang tham gia b i d ng ả ế ả ả ọ ồ ưỡ
Ch a làmư
đcượ Đã làm nh ng đnhư ị
h ng cách gi i saiướ ả Làm đc nh ngượ ư
ch a xongưLàm đc cượ ả
bài
SL % SL % SL % SL %
10 50,0% 03 15,0% 5 25,0% 2 10,0%
3
M t s sai l m và ph ng pháp kh c ph c khi gi i bài toán c c tr Đi sộ ố ầ ươ ắ ụ ả ự ị ạ ố
Qua công tác ch m ch a và tìm hi u h c sinh tôi nh n th y có m t sấ ữ ể ọ ậ ấ ộ ố
nguyên nhân nh sau:ư
- H c sinh ch a có đng l i rõ ràng khi gi i bài toán tìm c c tr Điọ ư ườ ố ả ự ị ạ
s .ố
- H c sinh ch a n m ch c các tính ch t c a b t đng th c vì bài toánọ ư ắ ắ ấ ủ ấ ẳ ứ
c c tr liên quan r t ch t ch v i bài toán ch ng minh b t đng th c.ự ị ấ ặ ẽ ớ ứ ấ ẳ ứ
- Ch a h th ng, phân lo i đc các d ng bài t p và ph ng pháp gi i.ư ệ ố ạ ượ ạ ậ ươ ả
- Không đc kĩ đu bài, ch a hi u rõ bài toán đã đã v i đi ngay vào gi iọ ầ ư ể ộ ả
toán.
- Không bi t đ c p bài toán theo nhi u cách gi i khác nhau, không ch uế ề ậ ề ả ị
nghiên c u kĩ t ng chi ti t và k t h p các chi ti t trong t ng bài toán, khôngứ ừ ế ế ợ ế ừ
s d ng h t gi thi t bài toán, không bi t linh ho t v n d ng ki n th c đã có.ử ụ ế ả ế ế ạ ậ ụ ế ứ
- Không t t duy l i bài toán mình làm sau khi đã gi i xong xem đãự ư ạ ả
đúng ch a.ư
Qua đó tôi rút ra đc m t s v n đ c n đc kh c ph c trong vi cượ ộ ố ấ ề ầ ượ ắ ụ ệ
đi m i ph ng pháp d y h c nh sau:ổ ớ ươ ạ ọ ư
- Ph i trang b cho h c sinh n m ch c ch n các ki n th c c b n v bàiả ị ọ ắ ắ ắ ế ứ ơ ả ề
toán tìm c c tr Đi s và các ki n th c c b n v b t đng th cự ị ạ ố ế ứ ơ ả ề ấ ẳ ứ
- Ph i phân lo i đc các d ng toán và xây d ng ph ng pháp gi i phùả ạ ượ ạ ự ươ ả
h p cho t ng d ng toán c c trợ ừ ạ ự ị
- Tìm ra các sai l m c b n và h ng kh c ph c cho t ng sai l m đóầ ơ ả ướ ắ ụ ừ ầ
- Yêu c u h c sinh th c hành t duy tìm h ng gi i và trình bày bàiầ ọ ự ư ướ ả
gi iả
V i đc tr ng c a công tác b i d ng h c sinh gi i tôi nh n th y cóớ ặ ư ủ ồ ưỡ ọ ỏ ậ ấ
nhi u thu n l i đ tri n khai nghiên c u, áp d ng sáng ki n: ề ậ ợ ể ể ứ ụ ế “M t s saiộ ố
l m và ph ng pháp kh c ph c khi gi i bài toán c c tr đi s ”ầ ươ ắ ụ ả ự ị ạ ố . Sau đây
tôi xin đa ra m t s gi i pháp:ư ộ ố ả
II. Các gi i pháp:ả
1, Gi i pháp 1: Trang b cho h c sinh các ki n th c c b n v c c trả ị ọ ế ứ ơ ả ề ự ị
Đi s cũng nh các ki n th c c b n v b t đng th c:ạ ố ư ế ứ ơ ả ề ấ ẳ ứ
1.1, Ki n th c c b n v c c tr đi s :ế ứ ơ ả ề ự ị ạ ố
1.1.1, Đnh nghĩa.ị
a, Đnh nghĩa GTNN (Min):ị Cho bi u th c m t bi n A(x) đc xác đnh trênể ứ ộ ế ượ ị
t p D. N u m i giá tr c a x ậ ế ọ ị ủ
D mà A(x)
m (v i m ớ R) (1), d u đngấ ẳ
th c x y ra t i x = xứ ả ạ 0 và x0 D (2) ta nói A(x) có giá tr nh nh t là k, t i x =ị ỏ ấ ạ
x0
4
M t s sai l m và ph ng pháp kh c ph c khi gi i bài toán c c tr Đi sộ ố ầ ươ ắ ụ ả ự ị ạ ố
Ký hi u: Min A(x) = m, t i x = xệ ạ 0
b, Đnh nghĩa GTLN (Max):ị Cho bi u th c m t bi n A(x) đc xác đnh trênể ứ ộ ế ượ ị
t p D. N u m i giá tr c a x ậ ế ọ ị ủ D mà A(x) ≤ n ( v i n ớ R) (1), d u đngấ ẳ
th c x y ra t i x = xứ ả ạ 0 và x0 D (2) ta nói A(x) có giá tr l n nh t là n, t i x =ị ớ ấ ạ
x0
Ký hi u: MaxA(x) = n, t i x = xệ ạ 0
c, Chú ý: - Hai đnh nghĩa trên v n đúng v i bi u th c hai bi n A(x; y) tr lênị ẫ ớ ể ứ ế ở
- Đ t n t i c c tr thì đi u ki n (1) và (2) đng th i th a mãnể ồ ạ ự ị ề ệ ồ ờ ỏ
Ví d minh h a: Ta xét bi u th c A = (x - 1)ụ ọ ể ứ 2 + (x - 3)2. Rõ ràng A
0, d uấ
b ng x y ra khi: ằ ả
x - 1 = 0 x = 1
x - 3 = 0 x = 3
� �
� �
� �
(đi u này vô lý). ề
Nên ta không th k t lu n MinA = 0 đc.ể ế ậ ượ
* Cách gi i đúng: ả
A = (x - 1)2 + (x - 3)2 = 2x2 - 8x + 10 = 2(x - 2)2 + 2
2
D u b ng x y ra khi x = 2. V y MinA = 2, khi x = 2.ấ ằ ả ậ
1.1.2, M t s tính ch t c a giá tr l n nh t và giá tr nh nh t c a hàmộ ố ấ ủ ị ớ ấ ị ỏ ấ ủ
s :ố
Tính ch t 1:ấ Gi s ả ử
A B
khi đó ta có:
a,
)(max)( xfxfMax
BxAx
b,
)(min)( xfxfMin
Bx
Ax
Tính ch t 2:ấ N u ế
0),( yxf
v i m i ớ ọ
x
thu c ộ
, ta có:
a,
)(max)( 2xfxfMax DxDx
b,
)(min)( 2xfxfMin Dx
Dx
Tính ch t 3:ấa,
( )
1 2
( ) ( ) ( ) ( )
x D x D x D
Max f x g x Max f x Max f x
� � �
+ +
)1(
b,
( )
1 2
( ) ( ) ( ) ( )
x D x D x D
Min f x g x Min f x Min f x
� � �
+ +
)2(
D u b ng trong ấ ằ
)1(
x y ra khi có ít nh t m t đi m ẩ ấ ộ ể
0
x
mà t i đóạ
)(xf
và
)(xg
cùng đt giá tr l n nh t. T ng t n u t n t i ạ ị ớ ấ ươ ự ế ồ ạ
0
x
thu c ộ
mà t i đó ạ
gf ,
cùng đt giá tr nh nh t thì ạ ị ỏ ấ
)2(
có d u b ng.ấ ằ
Tính ch t 4:ấ
1
x D
x D
Max f(x) = -min (-f(x))
Tính ch t 5: ấN u đt ế ặ
)(xfMaxM Dx
,
)(min xfm Dx
thì
mMMaxxfMax DxDx ,)(
.
Tính ch t 6: ấGi s ả ử
0)(;
1 xfDxD
và
0)(;
2 xfDxD
thì
)(min);(max)(
2
1
xfxfMinxfMin Dx
DxDx
5