
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO THỪA THIÊN HUẾ
TRƯỜNG THPT VINH LỘC
----------------------------
SÁNG KIẾN KINH NGHIỆM
Bộ môn: Toán học
Đề tài:
BÀI TOÁN KHOẢNG CÁCH QUA ĐỀ THI
ĐẠI HỌC
Họ và tên: Nguyễn Đắc Tuấn
Chức vụ: Giáo viên
Đơn vị: Trường THPT Vinh Lộc
Vinh Lộc, tháng 02 năm 2013

2
MỤC LỤC
Nội dung Trang
1. Đặt vấn đề 2
2. Giải quyết vấn đề (Nội dung sáng kiến kinh nghiệm) 2
3. Kết luận 16
4. Tài liệu tham khảo 17

3
1. Đặt vấn đề:
1.1. Lý do chọn đề tài.
a) Cơ sở lý luận:
Đổi mới phương pháp dạy học là sự thay đổi từ các phương pháp dạy học
tiêu cực (truyền thụ áp đặt, một chiều từ thầy giáo đến học sinh) đến các phương
pháp tích cực, sáng tạo (tổ chức, định hướng nhận thức, phát huy tính sáng tạo,
chủ động để học sinh tự chiếm lĩnh tri thức và kĩ năng). Nhưng không phải ngay
lập tức thay đổi bằng những phương pháp hoàn toàn mới lạ mà phải là một quá
trình áp dụng phương pháp dạy học hiện đại trên cơ sở phát huy các yếu tố tích
cực của phương pháp dạy học truyền thống nhằm thay đổi cách thức, phương
pháp học tập của học sinh chuyển từ thụ động sang chủ động. Một trong những
yếu tố phát huy tính tích cực, sáng tạo là dạy học có sự tham gia nhiệt tình, hưng
phấn của học sinh, giúp học sinh tìm ra cách học mới.
Như vậy giáo viên là người khơi nguồn và tạo ra sự hưng phấn, khám phá
cái mới trong học tập của học sinh: sưu tầm, soạn thảo một số cách giải khác
mới lạ và hay để học sinh trải nghiệm.
Hình học không gian là một trong những nội dung khó đối với học sinh
phổ thông. Trong các đề thi Đại học và Cao đẳng những năm gần đây thì các câu
hỏi về tính khoảng cách từ điểm đến mặt phẳng, khoảng cách giữa hai đương
thẳng chéo nhau thường xuyên có mặt.
b) Cơ sở thực tiễn:
Học sinh thường rất ngại với việc giải toán hình học không gian, đặc biệt
các bài toán về khoảng cách do các em nắm kiến thức hình học không gian
không tốt, một phần do đặc thù khó của nội dung này nên các em gặp rất nhiều
khó khăn khi giải các bài toán về khoảng cách trong các đề thi Đại học. Với
mong muốn cung cấp và hệ thống một số phương pháp về tính khoảng cách
giúp người học tiếp cận dễ dàng hơn với các bài toán về tính khoảng cách nên
tôi đã chọn đề tài này để nghiên cứu.
1.2. Phạm vi đề tài:
Đề tài đưa ra các phương pháp xác định và tính khoảng cách từ một điểm
đến một mặt phẳng, giữa hai đường thẳng chéo nhau bằng nhiều cách khác nhau.
4
I
M
C
B
A'
C'
B'
A
K
H
2. Nội dung sáng kiến kinh nghiệm
2.1. Các kiến thức chuẩn bị:
2.2. Các bài toán về tính khoảng cách trong các đề thi Đại học:
Bài 1 (Đại học khối D – 2009)
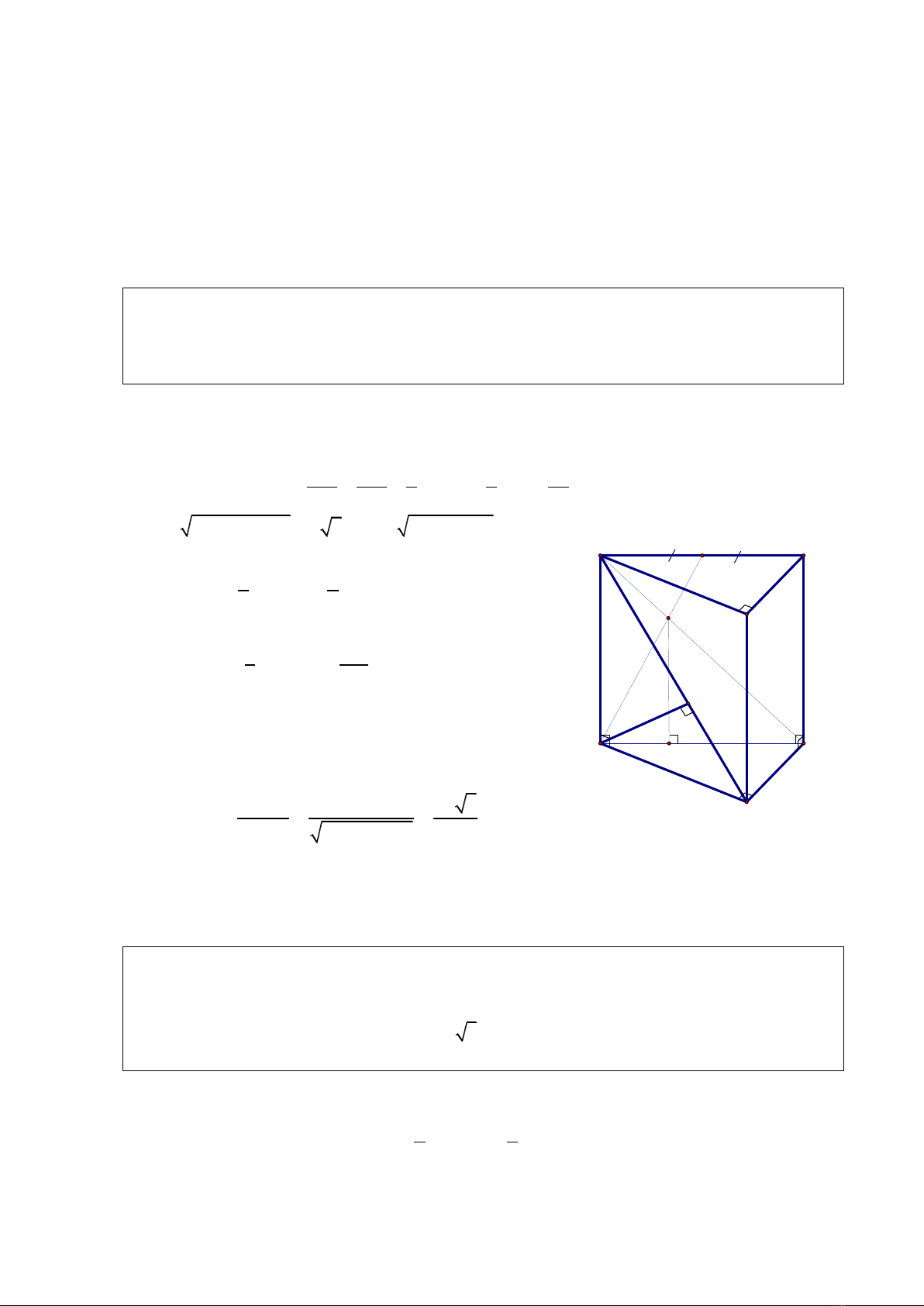
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB = a,
AA’ = 2a, A’C = 3a. Gọi M là trung điểm của A’C’, I là giao điểm của AM và A’C.
Tính theo a thể tích của khối tứ diện IABC và khoảng cách từ A đến mặt phẳng (IBC).
Bài giải.
* Tính thể tích của khối chóp IABC:
Hạ IH vuông góc với AC tại H. Ta có:
( )
;IH ABC⊥
IH là đường cao của tứ diện
IABC
2 2 4
/ / ' ' .
' ' 3 3 3
IH CI a
IH AA IH AA
AA CA
= = = =
2 2 2 2
' ' 5; 2 .AC A C A A a BC AC AB a= − = = − =
Diện tích tam giác ABC là:
2
11
. . . .2 .
22
ABC
S AB BC a a a= = =
Thể tích của khối tứ diện IABC là:
3
14
. . .
39
IABC ABC
a
V IH S==
* Tính khoảng cách từ A đến (IBC):
Hạ AK vuông góc với A’B tại K.
Vì
( )
''BC ABB A⊥
nên
( )
.AK BC AK IBC⊥ ⊥
Khoảng cách từ A đến (IBC) bằng AK.
Ta có:
'
22
2. '. 2 5 .
'5
'
AA B
SAA AB a
AK AB A A AB
= = =
+
Cách 2. Chọn hệ trục tọa như hình vẽ.
Bài 2. (Đề thi ĐH khối A - 2010)
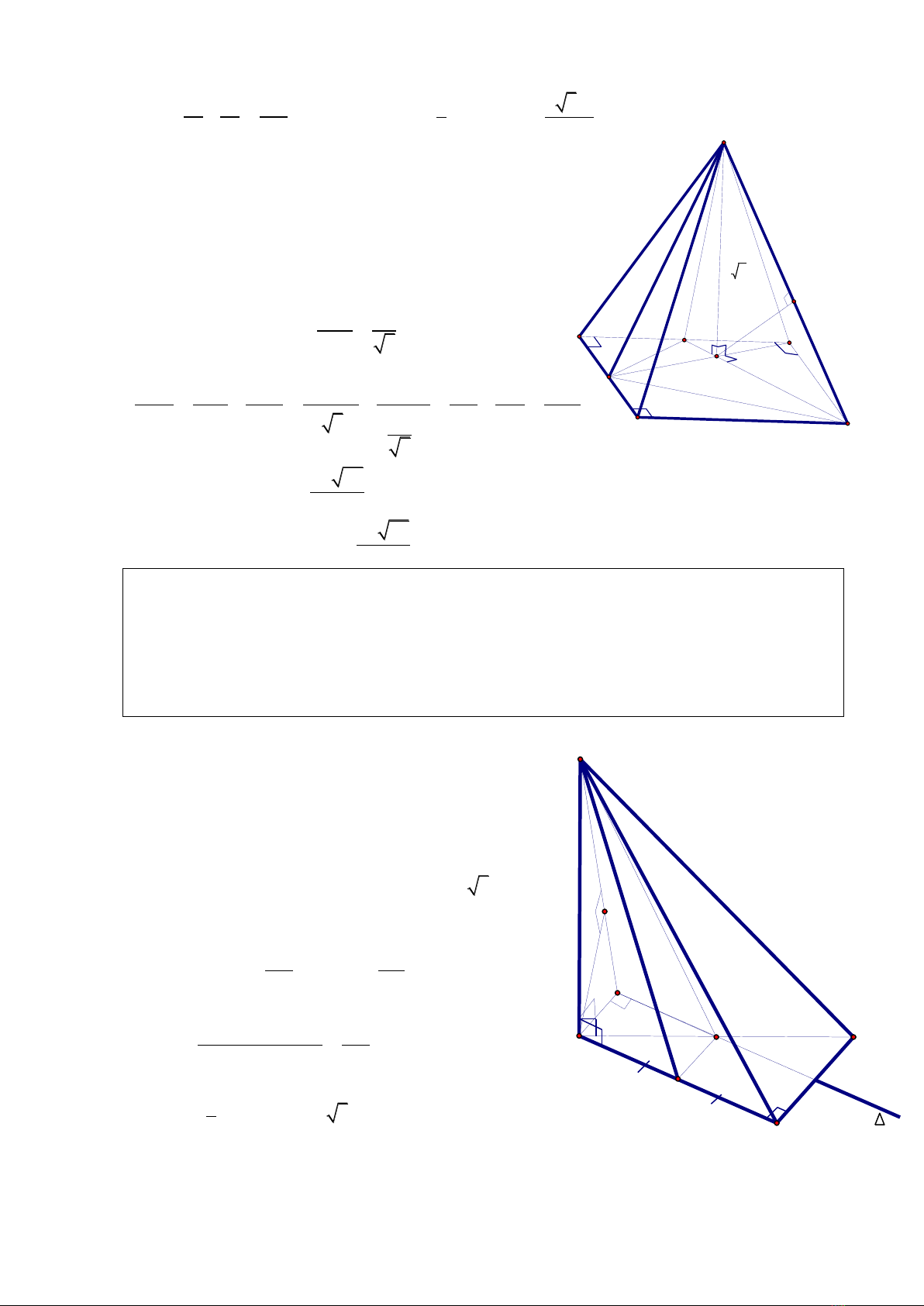
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M và N lần lượt là
trung điểm của các cạnh AB và AD; H là giao điểm của CN với DM. Biết SH vuông
góc với mặt phẳng (ABCD) và
3.SH a=
Tính thể tích khối chóp S.CDNM và tính
khoảng cách giữa hai đường thẳng DM và SC theo a.
Bài giải.
* Thể tích của khối chóp S.CDNM.
211
..
22
CDNM ABCD AMN BCM
S S S S AB AM AN BC BM= − − = − −
5
a
3
a
a
H
N
M
C
A
D
B
S
K
2 2 2
25.
8 4 8
a a a
a= − − =
Do đó:
3
.
1 5 3
. . .
3 24
S CDNM CDNM
a
V S SH==
* Khoảng cách giữa hai đường thẳng DM và SC.
,ADM DCN ADM DCN DM CN = = ⊥
kết hợp với
,DM SH⊥
suy ra:
( )
.DM SHC⊥
Hạ
( )
,HK SC K SC⊥
Suy ra HK là đoạn vuông góc chung của DM và SC, do đó:
( )
,.d DM SC HK=
Ta có tam giác vuông DCN, có DH là đường cao nên:
2
22
.5
CD a
CD HC CN HC CN
= = =
.
Tam giác SHC vuông tại H, có HK là đường cao nên
( )
22
2 2 2 2 2 2
1 1 1 1 1 1 5 19
3 4 12
2
3
5
HK SH HC a a a
a
a
= + = + = + =
2 57 .
19
a
HK=
Do đó:
( )
2 57
,.
19
a
d DM SC HK==
Bài 35. (Đề thi ĐH khối A – 2011)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B,
2;AB BC a==
hai
mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABC). Gọi M là trung
điểm của AB; mặt phẳng qua SM và song song với BC, cắt AC tại N. Biết góc giữa hai
mặt phẳng (SBC) và (ABC) bằng
0
60 .
Tính thể tích của khối chóp S.BCNM và khoảng
cách giữa hai đường thẳng AB và SN theo a.
Bài giải.
* Tính thể tích của khối chóp S.BCNM:
( )
SAB
và
( )
SAC
cùng vuông góc với (ABC)
nên suy ra:
( )
.SA ABC⊥
AB AC SB BC SBA⊥ ⊥
là góc giữa (SBC)
và (ABC).
Suy ra
00
60 .tan 60 2 3.SBA SA AB a = = =
Mặt phẳng qua SM và song song với BC, cắt
AC tại N. Suy ra: MN // BC và N là trung điểm
của AC.
,.
22
BC AB
MN a BM a= = = =
Diện tích của hình thang vuông BCNM:
( )
2
.3.
22
BCNM
BC MN BM a
S+
==
Thể tích của khối chóp S.BCNM là:
3
.
1. . 3
3
S BCNM BCNM
V S SA a==
(đvtt).
* Tính khoảng cách từ AB đến SN:
2a
2a
D
N
M
A
C
B
S
H



![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)










![Phiếu bài tập cuối tuần Tiếng Việt 1 tuần 2 đề 2: [Hướng dẫn chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250728/thanhha01/135x160/42951755577464.jpg)

