MỤC LỤC
I. ĐẶT VẤN ĐỀ.......................................................................................................
1 1. Lí do chọn đề
tài:............................................................................................... 1 2. Mục đích
của đề tài: .......................................................................................... 1 3. Nhiệm
vụ của đề tài: ......................................................................................... 1 4. Giới
hạn, phạm vi nghiên cứu của đề tài: ......................................................... 1
II. NỘI DUNG .........................................................................................................
2 1. Định nghĩa số nguyên tố:
.................................................................................. 2 2. Thuật toán Vét cạn
(Brute Forces).................................................................... 2 3. Sàng nguyên tố
Eratosthenes ............................................................................ 3 4. Cải tiến 1
........................................................................................................... 4 5. Cải tiến
2 ........................................................................................................... 5 6. Cải
tiến 3 ........................................................................................................... 5 Kết
quả sau cải tiến ............................................................................................... 7 7.
Một số bài toán ví dụ áp dụng........................................................................... 7
Bài 1: Factor.....................................................................................................
7 Bài 2. Tổng các số nguyên tố đầu tiên ............................................................
11 Bài 3. Tìm số nguyên tố thứ
N......................................................................... 12 Bài 4: Chú gấu Tommy và
các bạn ................................................................. 14 Bài 5: Hoán
đổi............................................................................................... 17 Bài 6:
Thuyền trưởng Prime ........................................................................... 20
III. KẾT LUẬN .....................................................................................................
25 TÀI LIỆU THAM KHẢO
.................................................................................... 26
I. ĐẶT VẤN ĐỀ
1. Lí do chọn đề tài:
Công tác tự học và tự nghiên cứu là một trong những hoạt động quan trọng
của giáo viên nhằm đáp ứng yêu cầu dạy học, đặc biệt là trong công tác bồi dưỡng
học sinh giỏi.
Đối với việc bồi dưỡng học sinh giỏi môn Tin học, có khá nhiều chuyên đề,
bài tập thường gặp trong các kỳ thi. Các bài toán về số học nói chung và số nguyên
tố nói riêng là một trong những bài tập thường gặp đó. Trong một số bài toán, ta rất
hay gặp các yêu cầu mà cần phải xác định được các số nguyên tố trong một phạm
vi giới hạn nào đó như: xét tính nguyên tố, liệt kê các số nguyên tố, đếm các số
nguyên tố,…
Sàng nguyên tố Eratosthenes là một thuật toán hiệu quả để kiểm tra, liệt kê,
đếm,… các số nguyên tố trong đoạn [1,N]. Tuy nhiên trong giới hạn thời gian 1
giây, nó chỉ thực sự hiệu quả khi N ≤ 107. Một cải tiến làm cho sàng
Eratosthenes có thể hiệu quả khi N ≤ 108trong giới hạn thời gian 1 giây để áp
dụng trong một số bài tập sẽ được trình bày trong sáng kiến này.
2. Mục đích của đề tài:
Trình bày về sàng Eratosthenes và cách cải tiến sàng Eratosthenes để áp dụng
giải một số bài toán liên quan.
3. Nhiệm vụ của đề tài:
• Trình bày sàng Eratosthenes và cải tiến sàng Eratosthenes.
• Một số bài tập áp dụng và hướng dẫn giải.
4. Giới hạn, phạm vi nghiên cứu của đề tài:
Đề tài sáng kiến nghiên cứu các cải tiến sàng Eratosthenes và áp dụng giải
một số bài toán trong chương trình bồi dưỡng học sinh giỏi Tin học tại trường
THPT Thanh Chương 1.
1
II. NỘI DUNG
1. Định nghĩa số nguyên tố:
Số nguyên tố là số tự nhiên lớn hơn 1 không phải là tích của hai số tự nhiên
nhỏ hơn. Nói cách khác, số nguyên tố là những số chỉ có đúng hai ước số là 1 và
chính nó. Các số tự nhiên lớn hơn 1 không phải là số nguyên tố được gọi là hợp số
Ví dụ: Số 11 là số nguyên tố do chỉ có 2 ước là 1 và 11. Số 9 không phải là số
nguyên tố do có 3 ước là 1, 3, 9.
2. Thuật toán Vét cạn (Brute Forces)
Đây là thuật toán sử dụng kỹ thuật vét hết tất cả các số lẻ và kiểm tra tính
nguyên tố của nó theo định nghĩa.
Code minh họa
#include <bits/stdc++.h>
using namespace std;
void Bruce_forces(long limit)
{
long count = 1;
bool isPrime = true;
for (long i = 3; i <= limit; i += 2)
{
for (long j = 3; j * j <= i; j += 2)
{
if ((i % j) == 0) { isPrime = false; break; }
}
if (isPrime) { count++; }
else isPrime = true;
}
cout<<count<<endl;
}
int main()
{
long limit = 10000000;
Bruce_forces(limit);
return 0;
}
Độ phức tạp: O((nn)/4)
2
3. Sàng nguyên tố Eratosthenes
Để tìm các số nguyên tố nhỏ hơn hoặc bằng số tự nhiên N bằng sàng
Eratosthenes, ta làm như sau:
• Bước 1: Tạo 1 danh sách các số tự nhiên liên tiếp từ 2 đến N: (2, 3, 4,..., N).
• Bước 2: số 2 là số nguyên tố đầu tiên. Loại bỏ (đánh dấu không phải là số nguyên
tố) các bội của 2.
• Bước 3: số 3 là số nguyên tố tiếp theo. Loại bỏ (đánh dấu không phải là số
nguyên tố) các bội của 3.
• Bước 4: Lặp lại việc tìm số nguyên tố k đầu tiên tiếp theo. Loại bỏ (đánh dấu
không phải là số nguyên tố) các bội của k (k≤N
2
)
Khi giải thuật kết thúc (k > N
2
), tất các số chưa bị đánh dấu trong danh sách là
các số nguyên tố cần tìm
Code minh họa:
bool prime[10000001];
void Era(int n)
{
memset(prime, true, n);
for (int k=2; k*k<=n; k++){
if (prime[k] == true){
for (int i=k*k; i<=n; i += k)
prime[i] = false;
3
}
}
}
Độ phức tạp: O(nloglogn)
Tổng kết so sánh hiệu năng
Thực nghiệm được thực hiện trên máy tính có cấu hình: Intel Core 2 (3.0
GHz), RAM 8GB, Windows 64 bit. Cho kết quả như sau:
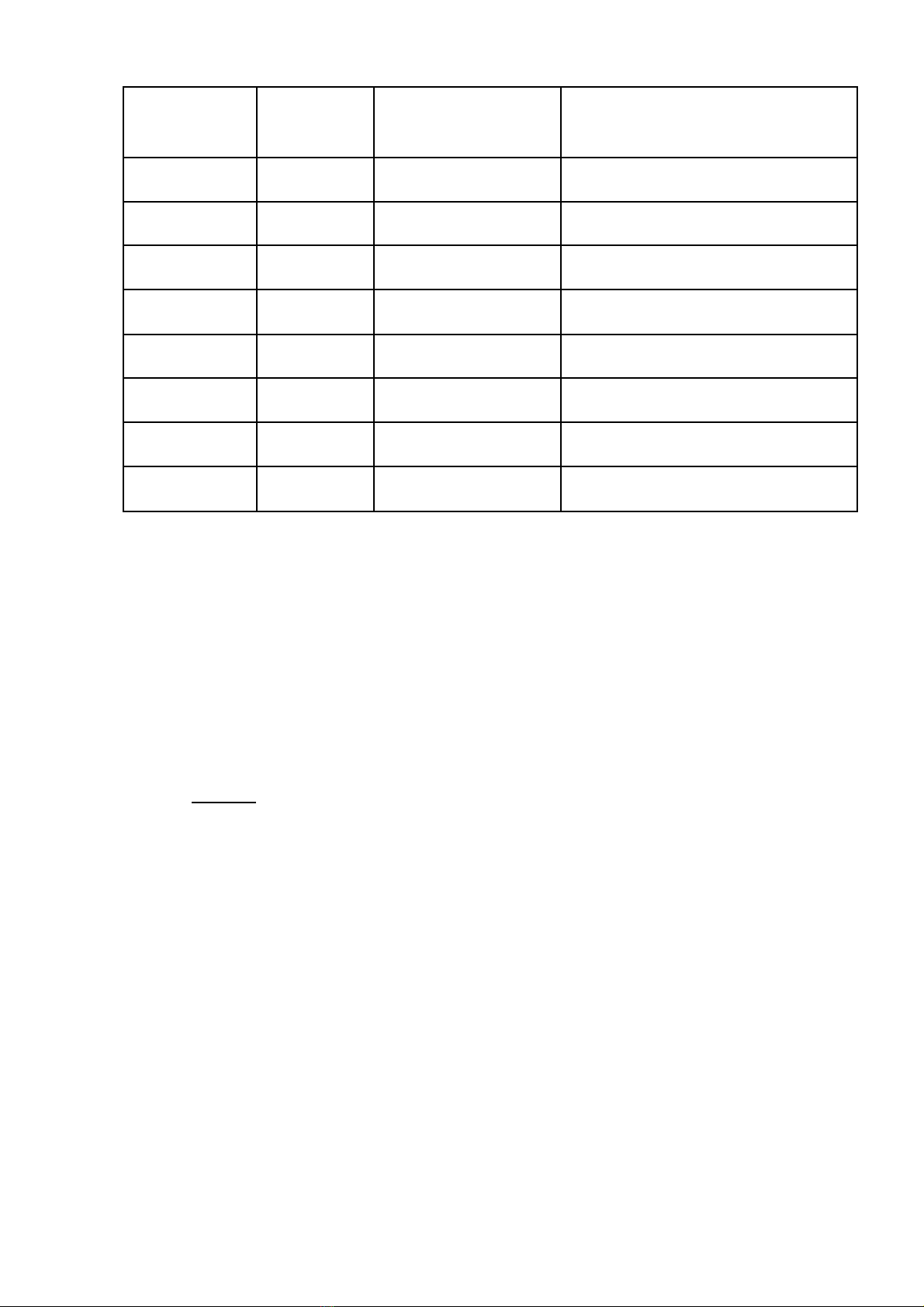
N
S
ố l
ư
ợng
SNT
Brute Force
Đ
ộ phức tạp
O((n√n)/4)
O(nloglogn)
1000
168
0.002
0.001
10000
1229
0.003
0.001
100000
9592
0.01
0.004
1000000
78498
0.124
0.013
10000000
664579
3.109
0.205
100000000
5761455
86.715
2.915
1000000000
50847534
TLE
32.924
Nhìn vào bảng thống kê ta thấy:
- V฀i n ≤ 106, chỉ cần thuật toán vét cạn thông thường ta có thể giải quyết
tốt bài toán đã nêu.
- Với n = 107, tất cả các thuật toán sàng nguyên tố đều làm tốt
- Với n = 108, 109 tất cả các thuật toán đều không thực hiện tốt. Trong số đó,
Sàng Eratosthenes là thuật toán cho kết quả tốt nhất, xấp xỉ 3s.
4. Cải tiến 1
Nhận xét: trừ số 2, tất cả các số chẵn đều không phải là số nguyên tố. Vì vậy
ta sẽ không xét đến các số chẵn trong thuật toán, khi đó không gian lưu trữ giảm
xuống còn n/2. Điều này sẽ làm giảm thời gian thực hiện thuật toán.
Code minh họa:
bool prime[10000001/2];
void Era1(int n){
memset(prime,true,n/2);
for (long long i = 3; i < n; i += 2) {
if (prime[i/2])//i la so nguyen to
{
for (long long j = i*i; j < n; j += 2*i)
4
prime[j/2] = false;